|
Чтобы понять всю сложность оценки производных финансовых инструментов до момента истечения, будет полезно взять на вооружение понятия, связанные с исчислением средних значений и предлагаемую концепцию вероятности. Это можно сделать с помощью простейшей арифметики. Не требуется никаких сложных математических подсчетов.


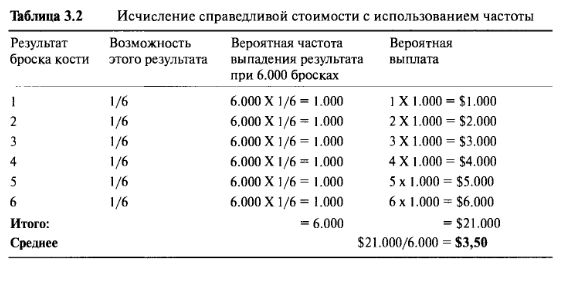
Представьте, что вы — в казино и играете в кости. Вы бросаете один кубик. Выплата будет равна тому количеству точек, которое окажется на верхней стороне кубика, когда он остановится. Если выпала единица, то вы получаете $1. Если двойка - то $2, и так далее. Максимум, что вы можете выиграть — это $6, и минимум — $1. Вопрос только в том, какую цену назначит казино за эту игру, если речь идет ни о прибыли, ни об убытке? Большинство читателей интуитивно назовут правильную сумму — $3,50, но нам лучше объяснить весь процесс вычисления "справедливой стоимости". Мы называем эту стоимость "справедливой", потому что если вы заплатите больше, то по истечении долгого периода времени вы, вероятнее всего, проиграете, но если заплатите меньше, то вероятнее всего, выиграете. Предположим, что игра повторяется 6.000 раз. Если игральный кубик без повреждений, то за это время одна шестая всех бросков придется на единицу, одна шестая на двойку, одна шестая на тройку и так далее. Таким образом, из 6.000 бросков 1.000 бросков, давших единицу, составят в итоге 1.000x1=$1.000. Точно также 1.000 бросков, давших двойку, составят 1.000х2=$2.000 и так далее. В Таблице 3.2 приведены все расчеты. Мы видим, что после 6.000 игр "ожидается" окончательная выплата, величина которой составляет $21.000. Таким образом, "средняя" выплата будет равна 21.000/6.000=$3,50 за одну игру. Поэтому, если бы мы играли в эту игру 6.000 раз и платили бы каждый раз $3,50 за участие в ней, тогда бы мы (и казино тоже) достигли уровня безубыточности. Если бы наш платеж составил $4 за каждую игру, тогда в среднем мы потеряли бы $0,50 за игру или в итоге: 6.000х0,50=$3,000. Если бы мы платили $3,20, тогда в среднем зарабатывали бы $0,30 за одну игру, что в итоге составило бы 6.000х0,30=$1.800.
В этом примере мы говорили об игре, продолжительность которой составила 6.000 бросков, потому что 6.000 удобно делится на 6. Также легко можно было бы "сделать" 60.000 бросков или 6 миллионов — результат был бы один и тот же: средняя выплата, а следовательно, справедливая цена составляет $3,50. Математики называют такие "будущие средние значения" или "ожидаемые средние значения" пока что нереализованных чисел ожидаемыми значениями (expected values). Сколько бы раз вы ни играли в эту игру, ожидаемое среднее значение все равно составит $3,50 за игру. Интересно то, что ни один бросок никогда не принесет вам ожидаемой выплаты, — то есть $3,50 никогда не будет оплатой одного броска. Эта цифра появится только как среднее значение за чрезвычайно продолжительный период времени.
В данном случае, учитывая, что игральный кубик не поврежден, все вероятностные результаты являются равновозможными. Такое распределение результатов называется нормальным (uniform). При таком нормальном распределении существует более легкий способ вычисления ожидаемой, или по-иному, справедливой стоимости. Чем бросать кости 6.000 раз, лучше представим, что кубик кидают 6 раз. Так как результаты равно-возможны, то предположим, что каждое число выпадает только один раз. Таким образом, единица предполагает выплату в $ 1, двойка в $2 и так далее. Это отражено в Таблице 3.3. При шести бросках общая выплата составляет $21. А $21 за шесть бросков означает 21/6=$3,50 за бросок.
Теперь представим себе эту игру по-другому. На этот раз при выпадении единицы или двойки выплачиваться ничего не будет. Какова тогда будет эта новая справедливая стоимость? Так как распределение все еще нормальное, то мы можем использовать простейший способ, показанный в Таблице 3.4.

Итак, в новой игре более низкое среднее значение за тот же длительный период — $3,00 за игру. Это неудивительно, так как два из шести бросков (единица и двойка) не требуют выплаты. Тип выплаты, который представлен в Таблице 3.4, напоминает что-то вроде опциона колл в день истечения его срока. Некоторые результаты являются нулевыми, а остальные — линейно увеличиваются.
Теперь мы используем этот тип доказательства, чтобы понять, каким образом опционы колл оцениваются до наступления окончания срока их обращения.

|