|
В этой главе мы ознакомимся с общепринятыми понятиями, используемыми в финансовом деле. Большинство читателей уяснят для себя, что означают такие термины, как длинная (лонг) и короткая (шорт) позиции, рыночная экспозиция, прибыль или убыток. Обсуждаемые вопросы затронут различные способы калькуляции цен опционов не математическим путем, и тогда будут использованы нестандартные термины. "Картина может рассказать тысячу историй" — выражение, дающее наилучшее представление о торговле волатильностью. Все вышеперечисленные термины и большинство сложных понятий будут объяснены с помощью графиков. Вы обнаружите, что для того, чтобы действительно понять торговлю волатильностью, надо уяснить такое понятие, как скорость изменения. Лучший способ понять, что такое скорость изменения (rates of change) — внимательно изучить рисунки.


2.1 Cкорость изменения и наклон прямых линий
В этом разделе мы будем изучать и измерять взаимосвязь, существующую между совокупностями переменных. Эта взаимосвязь является искусственной и отображается тремя способами: (1) в форме таблицы, (2) графически, (3) используя измерение скорости изменения. Каждый случай мы рассматриваем относительно двух воображаемых переменных: "X" и "У. И в каждом примере представляем, что "X" "толкает" "У, то есть "У зависит исключительно от "X", а "X" зависит от воздействия извне. Мы будем определять взаимосвязь, существующую между "У и "X", в том числе саму скорость, с которой "Y" меняется по отношению к "X". Это, в конце концов, приведет к реальным ситуациям, в которых "X" является ценой акции, а "У — стоимостью портфеля, содержащего акцию и производную ценную бумагу.
Портфель (на начальной стадии в любом случае) не подвержен риску, связанному с направлением цены акции. Выявление определенного соотношения между компонентами, принятие решения о том, что делать, когда акция, в конечном счете, начинает двигаться и как извлечь прибыль из волатильности, — темы, обсуждаемые в последующих главах. Но прежде чем мы перейдем к рассмотрению выше перечисленных вопросов, нам необходимо определить несколько общепринятых инвестиционных понятий.

Вначале изучите Таблицу 2.1, в которой приведен список шести установленных значений "X" и "У. Очевидно, что связь между "X" и "У абсолютна. Если рассматривать, как увеличивается значение "X": 100, НО, 120..., - можно увидеть, как увеличивается значение "Y": 200, 205, 210... Каждое изменение "У на 5 единиц явилось "следствием" изменения на 10 единиц значения "X". Рисунок 2.1 отражает ситуацию в графическом виде.
Соединение шести точек, чтобы провести прямую линию, является общепринятым способом, целью чего является показать связь между двумя переменными. Математики, по очевидным причинам, называют подобную взаимозависимость линейной (linear) взаимосвязью. Особенность линейных, или по-другому — прямолинейных взаимосвязей заключается в том, что они могут быть легко охарактеризованы одним простым показателем: отклонением или наклоном линии. Нарисуйте любой прямоугольный треугольник под или над прямой линией: наклон будет характеризовать пропорцию, определяющую соотношение между вертикальной и горизонтальной сторонами. На Рисунке 2.1 при использовании треугольника "ABC" пропорция составила 1 к 2. Наклоны, как правило, выражаются в виде коэффициентов соотношения или процентов, и, таким образом, наклон этой линейной взаимосвязи составляет:
Наклон = — = 0,50 (или 50%) 50
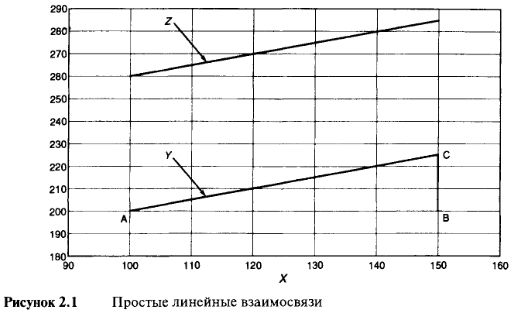
Конечно, этот ответ был очевиден, как следовало из Таблицы 2.1. Так как "X" увеличивается на 10, то "У увеличивается на 5. Если бы "X" увеличился на 5, то "У увеличился бы на 2,5. Если бы "X" увеличился на 1, то "У увеличился бы на 0,5. Короче говоря, скорость изменения "У по отношению к "X" равна 0,5, или 50%.
Таблица 2.1 также показывает значения третьей переменной "Z". По мере того, как "X" увеличивается от 100 к 110, к 120 и т.д., "Z" увеличивается от 260 к 265, к 270 и т.д. Переменная "Z" стартует с другого уровня по отношению к "У, но имеет точно такую же взаимосвязь с "X", то есть скорость изменения тоже равна 0,50. Графически это выглядит, как несколько параллельных линий. На Рисунке 2.1 мы видим, что наклоны обеих линий, несомненно, тождественны и равны 0,50. Способность обеих переменных к реагированию на изменения значений "X" одинакова. Важно понять, что действительное значение или уровень переменной, такой как "X" или "Z", зачастую не имеет значения. Скорость изменения значения по отношению к "X" — вот что действительно важно.
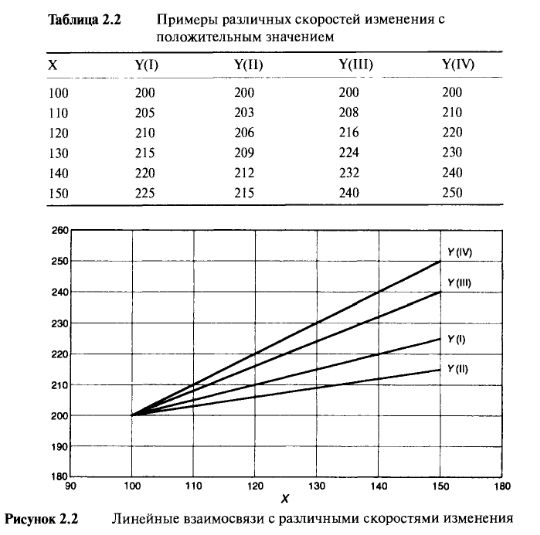
Рассмотрим Таблицу 2.2, в которой приведен перечень четырех воображаемых линейных взаимосвязей Y(I), Y(II), Y(III), Y(IV). Соответствующее графическое изображение дано на Рисунке 2.2. Сгруппированные числа и прямые линии, чьи наклоны различны, отражают тот факт, что взаимосвязи имеют различные степени изменения скорости. Взаимосвязь (I) подобна той, которая была рассмотрена выше, то есть "У увеличивается со скоростью 0,50 по отношению к "X". Что касается взаимосвязей (II), (III) и (IV), то скорости изменения равны 0,30, 0,80 и 1,00 соответственно. Более высокие скорости изменения представлены прямыми с более крутыми углами наклона
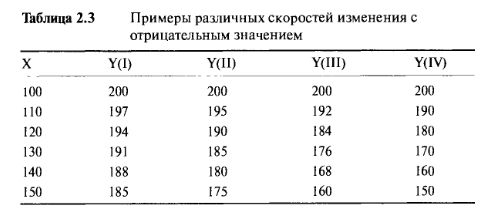
И, наконец, рассмотрим Таблицу 2.3 и Рисунок 2.3. Эти примеры показывают ситуации, в которых по мере того, как "X" увеличивается шажками по 10 единиц, шаги увеличения "У представляют собой разные значения.
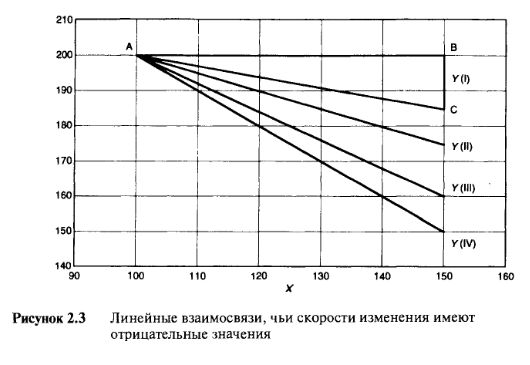
Здесь применяется тот же самый принцип измерения скорости изменения, за исключением того, что если направление изменения "У противоположно направлению изменения "X", то мы определяем наклон и скорость изменения как отрицательные величины. Итак, о взаимосвязи (I), в которой "У увеличивается на 3 единицы по мере того, как "X" увеличивается на 10 единиц, можно сказать, что величина наклона, или скорости изменения, равна 0,30. Графически это выглядит так же, за исключением того, что прямоугольный треугольник теперь уже нарисован основанием вверх, а длина вертикальной стороны ассоциируется со знаком минус. Основываясь на значениях Таблицы 2.3, мы можем вычислить наклон линии (I) из треугольника "ABC":
Наклон = — = 0,30 (или -30%) 50
Обратите внимание на то, что величина наклона, помимо всего прочего, определяет еще и крутизну. Линия (IV) имеет наклон "—1", или "—100%", и отражает взаимосвязь с максимальной скоростью изменения, хотя и в перевернутом смысле.
|