|
Эта таблица наиболее простая и возможно наиболее используемая. Она может быть задействована для расчета одноразовых стоимостей опциона, дельт, гамм, тэты и веги. Используя встроенный в Excel "What-if Problem Solver", можно также рассчитать подразумеваемую волатиль-ность опциона. Встроенные в Excel генераторы таблиц с вводом одного и двух значений (One-input and Two-input Data Table Solver) позволяют рассчитывать несколько параметров опциона и выводить их в виде графиков. Эта простая таблица может быть использована для демонстрации всех сложных свойств пут и колл опционов, описанных в этой книге, а также многих других, о которых не упоминалось вообще. Лучше понять, поведение опционов, можно, вводя различные данные о стоимости опционов и рассматривая результаты на графике. Ниже идет краткое описание порядка ввода данных в таблицу, а также расчеты. Примеры стоимостей, приведенные ниже, относятся к опциону, рассматриваемому на протяжении этой книги, а именно — одногодичному опциону колл около денег с волатильностью 15% и нулевой процентной ставкой.

Промежуточные переменные argl, arg2, ndl, ndl и ndll вычислены из вышеуказанных переменных с применением выражений:

Функция NORMDIST() вычисляет кумулятивное нормальное распределение и в результате получается число между нулем и единицей. Функция Р1( ) поддерживает математическую константу 'V. LN( ) есть натуральный логарифм, ЕХР( ) — экспонента аргументов , a SQRT( ) вычисляет квадратный корень.



Мы интерпретируем значения исходных данных следующим образом:
-Цена опциона колл (Call Option) $5,98 за одну акцию. Следовательно, если опцион на 100 акций, то стоимость опциона будет составлять $598.
-Дельта опциона колл (Call Delta) равна 0,53. Небольшое изменение в цене базовой акции изменит стоимость опциона на 53% в результате небольшого изменения. В качестве упражнения увеличьте цену акции на $0,10, до $100,10 и посмотрите, как это повлияет на цену опциона. Цена опциона должна будет увеличиться на 0,53 х 0,10 = $0,053. Новая цена составит $6,03 — в точности, как предсказывалось дельтой. Такая корректность наблюдается только при небольших изменениях.
-Вега опциона колл (Call Vega) равна 0,40. Небольшое изменение (создаваемое параметром сдвига по веге на 1% или 0,01) изменит цену опциона на $0,40 за акцию. В качестве упражнения, увеличьте параметр во-латильности от 15 до 16%. Обратите внимание, что новая цена опциона равна $6,38 — она увеличилась точно на $0,40. Как и со всеми скоростями изменения, это действительно только при небольших сдвигах в волатильности. Для того чтобы узнать, какое влияние может оказать значительное изменение, например на 10%, просто измените параметр волатильности.
-Тэта опциона колл (Call Theta) равна —0,0082. Параметр сдвига во времени в этом примере установлен на очень небольшое значение — 1 день (= 1/365 = 0,00274 года). Результат значения тэта колл говорит нам о том, что по мере прохождения одного дня опцион теряет в стоимости $0,0082 за акцию. Если параметр сдвига во времени установить на одну неделю (= 1/52 = 0,0192 года), тэта изменится на —0,0574, что почти в семь раз отличается от тэты, которая установлена для одного дня. При сроке в один год до наступления срока истечения распад тэты почти линейный.
-Дельта от Беги: del (vega) равна 0,001989 или приблизительно 0,002. Если волатильность опциона увеличится на значение сдвига по веге (1% в этом примере), тогда дельта опциона увеличится на 0,002. При вола-тильности, установленной на значении 15%, дельта равна 0,5299, поэтому 10 опционов, исполняемые на 100 акций, будут экспонировать 100 х 100 х 0.5299 = 5.299 акций. Изменение в дельте, вызванное увеличением в волатильности до 16%, увеличит экспозицию акции на 100 х 100 х 0,002 = 20 акций до 5.319.
-Тэта от дельты del (theta) равна —0,00004087. Прохождение одного дня сокращает дельту опциона на это очень маленькое значение.
-Гамма (Gamma) равна 0,002652. Переменная значения сдвига в акции установлена на $0,10. Гамма в результирующей переменной дает изменение дельты, вызванное изменением в цене базовой акции на $0,10. В этом случае портфель, содержащий 100 опционов, исполняемых на 100 акций, будет иметь экспозицию 5.299 акций. Если цена базовой акции увеличилась от $100,00 до $100,10, тогда экспозиция акции увеличится на 100 х 100 х 0,002652 = 26 акций до 5.325.
Соответствующие переменные опциона пут (Put Option) и образцы стоимостей рассчитываются из значении опциона колл:

Использование таблицы с одним вводным значением для создания таблиц и графиков
Чтобы посмотреть, как изменения в одной переменной влияют на одно или более свойств опциона, используйте таблицу Microsoft Excel с одним вводным значением. Пример, находящийся в файле OPTIONS.XLS, показывает, как цена и дельта одногодичного опциона колл изменяются относительно цены базовой акции. Таблица с данными составлена так, что диапазон J13...J25 содержит различные цены акции: 70, 75, 80,..., 130. Ячейки К12 и L12 содержат формулу: [=call] и [=ndl] соответственно. Для того чтобы создать таблицу, содержащую цену опциона колл и дельту колл на каждом уровне цены акции, сначала надо выбрать прямоугольный диапазон (J12...L25). Затем выберите Table из меню Data. Вводимый параметр, который должен будет варьироваться в этом примере, является ценой акции, и в ядре таблицы цена акции введена в ячейку С4. Как только действительные значения переменной появились в колонке, определите С4 как Column Input Cell и выберите ОК. Две колонки стоимостей, соответствующих цене опциона колл и дельте колл, появятся в диапазонах (К13...К25) и (L13 ...L25) соответственно. Вывести результаты на график несложно. Чтобы разобраться детально, рассмотрите Рисунок А1.

Можно расширить способности таблицы с одним вводным значением путем включения любого количества формул. Можно включить в таблицу результирующие значения веги, тэты и гаммы, чтобы увидеть, как эти значения изменяются вместе с ценой базовой акции.
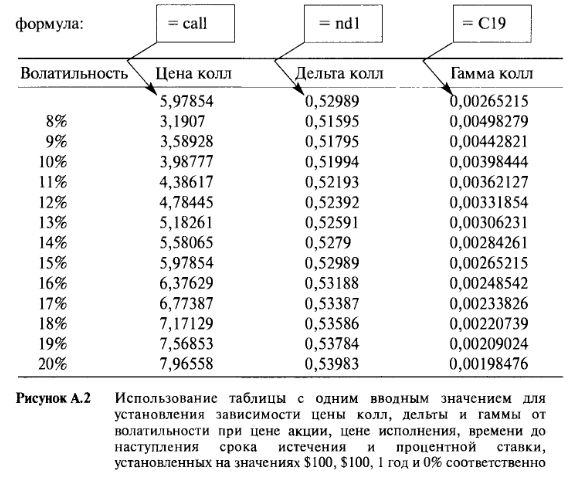
Таблицы и Рисунки, полученные с помощью этого метода, показывают, как цена опциона, дельта, вега и т.д. изменяются относительно цены базовой акции. Совсем нетрудно показать, как эти свойства изменяются относительно любой другой переменной. Вводя различные значения волатильности, скажем 8%, 9%, 10%.., внутри диапазонаJ 12...J25) и указывая. значение в С6 (ячейка для ввода волатильности), можно увидеть, как все вышеуказанные результирующие значения зависят от волатильности данной акции. Рисунок А.2 показывает, как цена, дельта и гамма опциона колл изменяются вместе с волатильностью.
Применение подобного подхода позволит установить зависимость каждого из свойств опциона от времени до наступления срока истечения, процентных ставок, цены исполнения.
Использование таблицы с двумя вводными значениями для создания таблиц и графиков
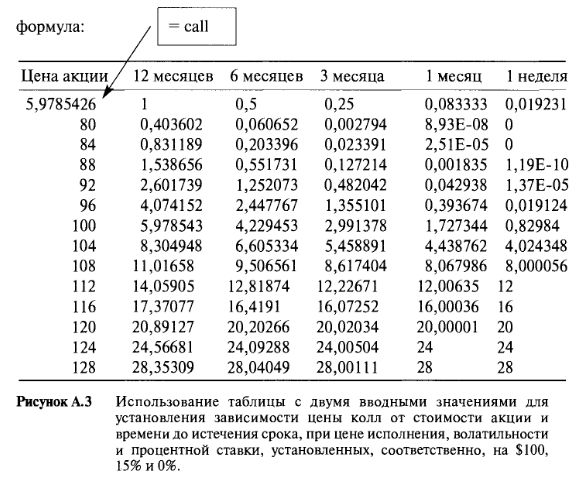
Чтобы увидеть, как изменения в двух переменных влияют на свойства опциона, используйте таблицу Microsoft Excel с двумя вводными значениями. Пример, находящийся в файле OPTIONS.XLS, показывает, как получается график на Рисунке 4.11, демонстрирующий влияние временного распада на цену опциона, дельту и гамму при различных ценах акции. Таблица данных установлена внутри области (N12...S25). Цены акции: 80, 84, 88 ... находятся в колонке, включенной в область (N13...N25). Пять разных значений времени до срока истечения: 12 месяцев, 6 месяцев, три месяца, 1 месяц и 1 неделя находятся в одном ряду, в области (012...S12). Ячейка N12 содержит формулу: [= call]. Сначала выберите область данных (N12...S25). Затем выберите Table из меню Data. Параметрами вводных значений, которые должны изменяться в этом примере, являются цена акции и время до наступления срока истечения. Цена акции вводится в ячейку С4, а время до срока истечения вводится в ячейку С7. Как только значения переменной цены акции появились в колонке, определите С4, как Column Input Cell и, как только значения переменной времени до срока истечения появятся в ряду, определите С7, как Row Input Cell. Выберите кнопку ОК. Появится двумерная таблица, содержащая значения, соответствующие ценам опциона. Вывести на график результаты и получить первое изображение, представленное на Рисунке 4.11, несложно. Чтобы узнать подробности, обратитесь к Рисунку А.З.
Для создания двумерной таблицы различных значений дельты, нужно просто изменить формулу в ячейке на формулу [=ndl]. Для получения различных значений гаммы, измените формулу в ячейке на [=С19].
Нахождение подразумеваемой волатильности с помощью "What-if-Solver"
Теоретическая стоимость опциона зависит (обычно) от пяти вводных значений: цены акции, цены исполнения, процентной ставки, времени до срока истечения и параметра волатильности. Первые четыре значения известны, поэтому определить их достаточно просто. Параметр волатильности неизвестен и часто рассчитывается с помощью исторического анализа. Но также можно сделать субъективное предположение о том, какова будет волатильность в будущем. Подставляя пять значений в модель, находящуюся в файле OPTION. XLS, вы получите цену опциона, дельту и так далее. Нелишне будет задать себе и такой вопрос: если сегодня рыночная цена опциона такая-то, то какую волатильность в будущем она подразумевает? Другими словами, какое нужно ввести значение волатильности в модель, чтобы получить теоретическую цену, которая, в свою очередь, точно совпадает с рыночной ценой, то есть какова подразумеваемая волатильность опциона?
Одним из способов решения является попытка повторного использования (подбора) различных значений волатильности в ячейке С6 до тех пор, пока теоретическая цена опциона (в ячейке С12 для колл опционов или ячейке G12 для пут опционов) в точности не совпадет с рыночной ценой. Это сработает, но процесс подбора может оказаться чрезвычайно утомительным. Главное преимущество использования Microsoft Excel состоит в том, что в этой программе есть специальная функция, которая может быстро решить такого рода проблему, — команда "Goal Seek Command". У нас есть формула, дающая теоретическую стоимость опциона при вычислении значения волатильности. Мы знаем результат формулы (рыночная цена опциона), но не знаем вводного значения, подходящего для формулы, чтобы получить нужный результат. Команда "Goal Seek Command" меняет значение в обозначенной вами ячейке до тех пор, пока формула, зависящая от ячейки, не предоставит нужный вам результат.
В примере OPTIONS.XLS формула для опциона колл находится в ячейке С12, а неизвестная волатильность находится в ячейке Сб. Допустим, что нам необходимо определить подразумеваемую волатильность одногодичного опциона колл около денег, когда цена не $5,98, а $7,0. Выберите в меню Tools команду Goal Seek. В ячейку Set Cell введите С12. В То Value box введите 7,5 (вы устанавливаете такие значения волатильности для формулы, данной в С12, чтобы она была равна 7,5). Введите в By Changing box C6 и нажмите ОК. Результат очень быстро появится и будет равен 18,83%. Итак, если значение волатильности 18,83% введено в модель, то теоретическая цена опциона равна $7,5. Подразумеваемая волатильность опциона равна 18,83%. При небольшом навыке все очень просто.
|