|
На практике, при построении биномиального дерева, отражающего изменение цены акции, для оценки ее волатильности используются параметры и и d. Чтобы понять, как это происходит, обозначим ожидаемую доходность акции (в реальном мире) через μ, а ее волатильность – через σ. На рис. 11.9, а продемонстрировано изменение цены акции в момент первого разветвления биномиального дерева. Длина шага по времени равна Δt. Цена акции либо увеличивается на величину, пропорциональную первоначальной сумме с коэффициентом u, либо уменьшается на величину, пропорциональную первоначальной сумме с коэффициентом d. Вероятность изменения цены акции в реальном мире равна р*.
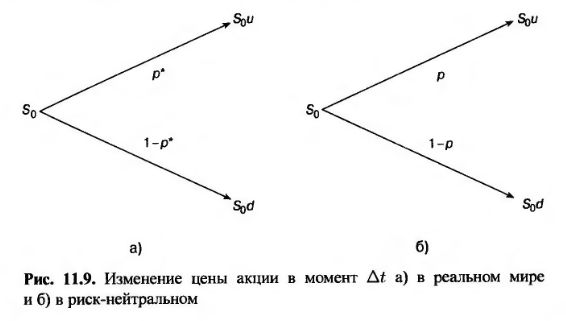


Цена акции, ожидаемая в конце первого расчетного интервала, равна S0eμ Δt. На биномиальном дереве цена акции, ожидаемая в этот момент, равен
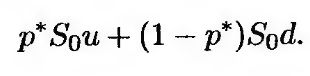
Чтобы сопоставить цену акции, ожидаемую в конце первого расчетного интервала, и цену акции, вычисленную с помощью биномиального дерева, запишем следующее уравнение.
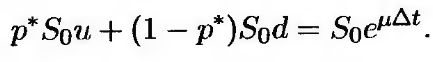
Отсюда следует, что
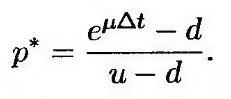 (11.11) (11.11)
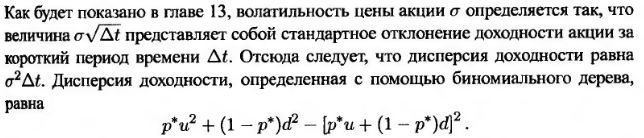
Чтобы сопоставить волатильность цены акции с параметрами дерева, составим следующее уравнение.
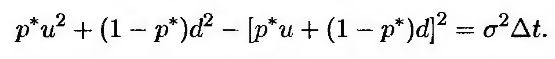 (11.12) (11.12)
Подставляя выражение (11.9) в формулу (11.10), получаем
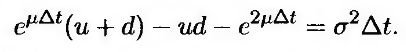
Отбрасывая слагаемые, содержащие множитель Δt2 и более высокие степени величины Δt, решение этого уравнения можно записать в следующем виде.
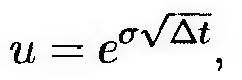 (11.13) (11.13)
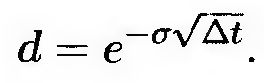 (11.14) (11.14)
Эти формулы для вычисления параметров u и d были предложены Коксом, Россом и Рубинштейном (1979).
Анализ, проведенный в этой главе, показывает, что при оценке опциона дерево, изображенное на рис. 11.9, а, можно заменить деревом, изображенным на рис. 11.9, б, в котором вероятность роста цены акции равна р, а затем выполнять вычисления в соответствии с риск-нейтральной моделью. Величина р, представляющая собой риск-нейтральную вероятность роста акций, вычисляется по формуле (11.3), т.е.
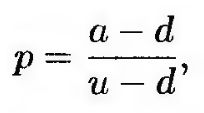 (11.15) (11.15)
где
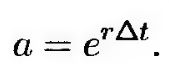 (11.16) (11.16)
На рис. 11.9, б видно, что ожидаемая цена акции в конце расчетного интервала равна S0erΔt, что соответствует формуле (11.4). Дисперсия цены акции равна
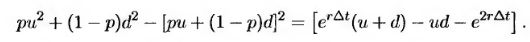
Подставляя вместо u и v выражения (11.13) и (11.14) и отбрасывая члены, содержащие множитель Δt2 и более высокие степени величины Δt, получаем, что эта дисперсия равна σ2 Δt.
Анализ показывает, что при переходе из риск-нейтрального мира в реальный ожидаемая доходность акции изменяется, однако ее волатильность остается прежней (по крайнем мере при величине Δt, стремящейся к нулю). Этот результат называется теоремой Гирсанова (Girsanov's theorem). При переходе их мира с одним набором рисковых предпочтений в мир с другими предпочтениями, ожидаемая скорость роста переменных также изменяется, но их волатильность по-прежнему остается неизменной. Более детально это явление исследуется в главе 25. Переход от одной системы рисковых предпочтений к другой иногда называется изменением меры (changing the measure). Мера, применяемая в реальном мире, иногда называется Р-мерой (P-measure), а мера, используемая в риск-нейтральном мире, – Q-мерой (Q-measure).
Вернемся к американскому опциону "пут", оцененному с помощью дерева, изображенного на рис. 11.8. В этом варианте цена акции равна 50 долл., цена исполнения – 52 долл., безрисковая процентная ставка – 5%, продолжительность опциона – 2 года. Кроме того, для построения биномиального дерева использовано два шага по времени. В данном случае Δt = 1. Предположим, что волатильность σ равна 30%. Тогда из формул (11.13)-(11.16) следует, что
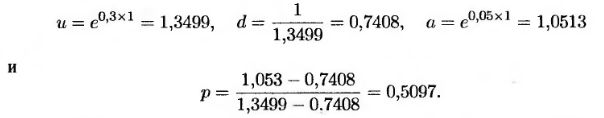
Соответствующее дерево изображено на рис. 11.10. Стоимость опциона "пут" равна 7,43 долл. Эта сумма отличается от стоимости опциона, вычисленной с помощью дерева, представленного на рис. 11.8, поскольку ранее мы предполагали, что u = 1,2 и d – 0,8.
|