|
Покажем, что лемму Ито можно интерпретировать как естественное обобщение более простых результатов. Рассмотрим непрерывную и дифференцируемую функцию G, зависящую от переменной х. Если величина Δх представляет собой малое изменение переменной х, a ΔG – соответствующее малое изменение функции G, то, как известно из классического математического анализа,
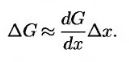 (12.1.1) (12.1.1)


Иначе говоря, величина ΔG приближенно равна скорости изменения функции G, умноженной на приращение переменной х. Ошибка этого равенства пропорциональна величине Δх2. Для большей точности можно использовать ряд Тейлора.
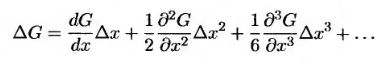
Для непрерывной и дифференцируемой функции G, зависящей от двух переменных х и у, можно аналогично получить приближенное равенство
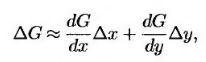 (12.1.2) (12.1.2)
и ряд Тейлора
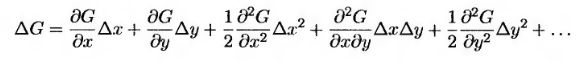 (12.1.3) (12.1.3)
Переходя в выражении (12.1.3) к пределу при Δх → 0 и Δу → 0, получим следующее уравнение.
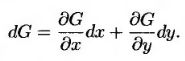 (12.1.4) (12.1.4)
Обобщим это уравнение на функции, зависящие от случайных переменных, описываемых процессами Ито. Допустим, что переменная х в уравнении (12.1.4) следует процессу Ито, т.е.
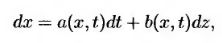 (12.1.5) (12.1.5)
а функция G зависит от переменной х и времени t. Аналогично выражению (12.1.3), можно записать следующее равенство.
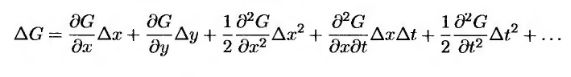 (12.1.6) (12.1.6)
Уравнение (12.1.5) можно дискретизировать следующим образом.
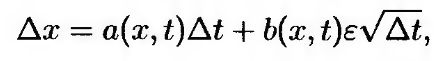
или
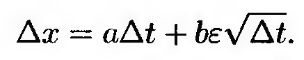 (12.1.7) (12.1.7)
Это уравнение выявляет важное различие между уравнениями (12.1.6) и (12.1.3). С одной стороны, при предельном переходе в уравнении (12.1.4) члены, зависящие от Δх2, можно было отбросить, поскольку они имели второй порядок. С другой стороны,
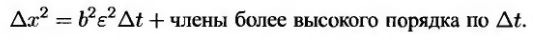 (12.1.8) (12.1.8)
Таким образом, в уравнении (12.1.6) член, содержащий величину Δt2, отбросить нельзя, поскольку одновременно он содержит компонент первого порядка.
Дисперсия стандартизованного нормального распределения равна 1,0. Это значит, что

Именно это и утверждает лемма Ито. Если подставить в уравнение (12.1.9) величину dx из уравнения (12.1.5), получим следующее равенство.
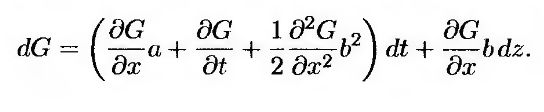
|