|
17.6 Моделирование по методу Монте-Карло
Метод Монте-Карло представляет собой совершенно иной метод оценки де-ривативов. Идея метода Монте-Карло продемонстрирована во врезке "Пример из деловой практики 17.1".


Пример из деловой практики 17.1. Вычисление числа "пи" с помощью метода Монте-Карло
Предположим, что длина сторон квадрата на рис. 17.13 равна единице. Представьте себе, что вы случайным образом бросаете дротик в этот квадрат и вычисляете долю попаданий. Что выясняется? Площадь квадрата равна 1,0, а радиус круга равен 0,5. Площадь круга равна произведению числа π и квадрата радиуса круга, т.е. π/4. Таким образом, число π можно приближенно вычислить, умножив долю попаданий в круг на число 4.
Для моделирования случайного бросания дротика можно использовать программу Excel, как показано в табл. 17.1. Введем в ячейки А1 и В1 формулу =СЛЧИС (). Таким образом, в этих ячейках будут записаны случайные числа, лежащие в диапазоне от 0 до 1. Они будут определять координаты точек попадания дротиков в квадрат, изображенный на рис. 17.13. В ячейку С1 введем формулу

Это позволит записать в ячейку С1 число 4, если дротик попал в квадрат, и 0 – в противном случае.
Остальные 99 строк рабочего листа заполняются аналогично. (Для этого можно использовать операцию "выбрать и перетащить" ("select and drag").) В ячейку С102 запишем формулу =СРЗНАЧ(С1:С100), а в ячейку С103 – формулу =СТАНДОТКЛОН (CI: C100). Таким образом, ячейка С102 содержит оценку числа π, вычисленную после 100 случайных испытаний (в табл. 17.1 эта оценка равна 3,04). Ячейка С103 содержит стандартное отклонение выборочных значений. Как показано в примере 17.1, эту величину можно использовать в качестве оценок точности приближенных вычислений. Увеличивая количество случайных испытаний, можно повысить точность, однако скорость сходимости к правильному значению 3,14162 невелика.

Метод Монте-Карло использует риск-нейтральные оценки. Размер ожидаемых выплат в риск-нейтральных условиях вычисляется с помощью метода выборочного исследования. После этого к нему применяется дисконтная ставка, равная безрисковой процентной ставке.
Рассмотрим дериватив, зависящий от единственного рыночного показателя S. Предположим, что выплаты по деривативу проводятся в момент Т. Предполагая, что процентные ставки являются постоянными, вычислим цену дериватива следующим образом.
1. Генерируем случайную траекторию величины S в риск-нейтральных условиях.
2. Вычисляем размер выплат по деривативу.
3. Повторяем шаги 1 и 2 многократно и получаем большое количество размеров выплат по деривативу в риск-нейтральных условиях.
4. Вычисляем среднее значение всех выборочных размеров выплат и оцениваем математическое ожидание размера выплат в риск-нейтральных условиях.
5. Применяем к вычисленной оценке математического ожидания выплат ставку дисконта на уровне безрисковой процентной ставки и получаем оценку стоимости дериватива.
Допустим, что в риск-нейтральных условиях базовый рыночный показатель подчиняется следующему стохастическому процессу.

Здесь S(t) – значение показателя S в момент t, а ε - случайное число из генеральной совокупности, имеющей нормальное распределение с нулевым математическим ожиданием и единичным стандартным отклонением. Это позволяет нам вычислить значение показателя S в момент Δt с помощью первоначального значения S, значение показателя S в момент 2Δt – с помощью значения S в момент Δt и т.д. Иллюстрация этой процедуры приведена в разделе 12.3. Один сеанс моделирования состоит из построения полной траектории величины S на основе N выборок из генеральной совокупности с нормальным распределением. На практике, как правило, моделируют величину In S, а не сам показатель S. Из леммы Ито следует, что стохастический процесс, описывающий поведение величины In S, имеет следующий вид.
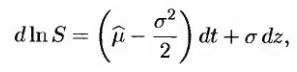 (17.15) (17.15)
так что
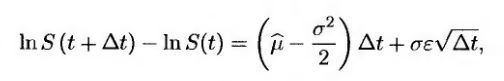
т.е.
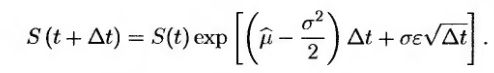 (17.16) (17.16)
Это уравнение используется для моделирования траектории величины S.
Преимущество работы с величиной In S заключается в том, что она подчиняется обобщенному винеровскому процессу.
Это значит, что формула
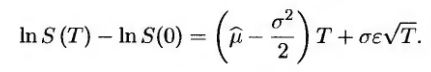
справедлива при всех значениях T. Следовательно,
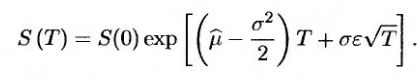 (17.17) (17.17)
Эту формулу можно использовать для оценки деривативов, предусматривающих нестандартные выплаты в момент Т. Кроме того, как указано во врезке "Пример из деловой практики 17.2", с ее помощью можно проверить формулы Блэка-Шоулза.
|