|
Если портфель содержит опционы, линейная модель становится приближенной. Она не учитывает коэффициент гамма инвестиционного портфеля. Как указывалось в главе 15, коэффициент дельта представляет собой скорость изменения стоимости портфеля по отношению к изменениям значений базового рыночного показателя, а коэффициент гамма – скорость изменения коэффициента дельта по отношению к изменениям значений базового рыночного показателя. Коэффициент гамма измеряет кривизну зависимости между стоимостью портфеля и базовым рыночным показателем.
На рис. 18.3 продемонстрировано влияние ненулевого коэффициента гамма на распределение вероятных значений стоимости портфеля. Если коэффициент гамма положителен, распределение вероятностей имеет положительную асимметрию. Если же коэффициент гамма является отрицательным, распределение гамма имеет отрицательную асимметрию.


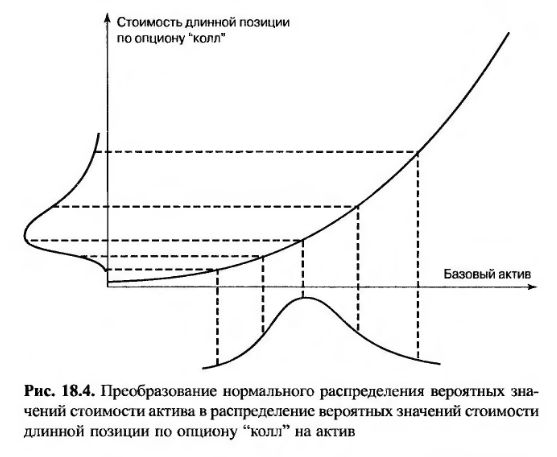
Причины этого явления показаны на рис. 18.4 и 18.5. На рис. 18.4 продемонстрирована зависимость между стоимостью длинной позиции по опциону "колл" и ценой базового актива. Длинная позиция по опциону "колл" – это пример опционной позиции с положительным коэффициентом гамма. Как показывает анализ рисунка, если стоимость базового актива в конце дня имеет нормальное распределение, то распределение вероятных значений стоимости опциона имеет положительную асимметрию.
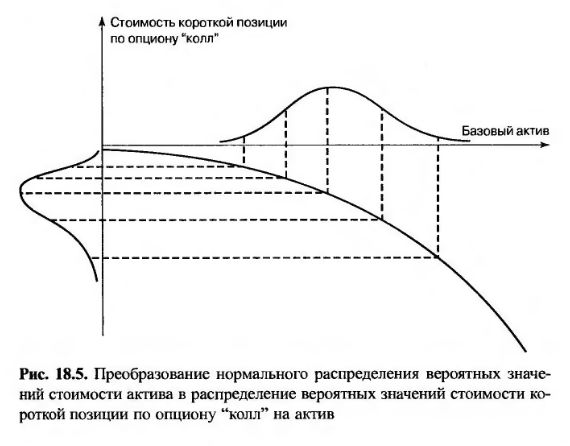
На рис. 18.5 показана зависимость между стоимостью короткой позиции по опциону "колл" и ценой базового актива. Короткий опцион "колл" – это пример опционной позиции с отрицательным коэффициентом гамма. Как показывает анализ рисунка, если стоимость базового актива в конце дня имеет нормальное распределение, то распределение вероятных значений стоимости опциона имеет отрицательную асимметрию.
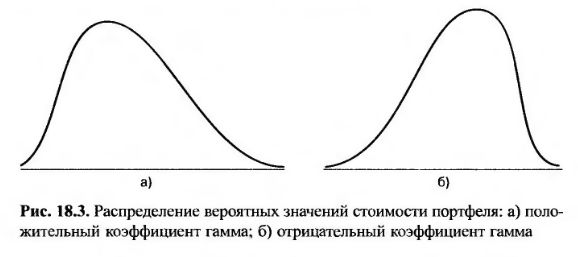
Показатель VaR инвестиционного портфеля чрезвычайно сильно зависит от левого хвоста распределения вероятных значений его стоимости. Например, если доверительный уровень равен 99%, показатель VaR равен значению, отсекающему от левого хвоста фигуру, площадь которой равна 1% всей площади, ограниченной плотностью вероятностей. Как показано на рис. 18.3, а и 18.4, распределение вероятных цен портфеля с положительным коэффициентом гамма имеет более легкий левый хвост, чем нормальное распределение. Если предположить, что распределение вероятных цен портфеля является нормальным, оценка показателя VaR окажется слишком завышенной. Аналогично, как показано на рис. 18.3, б и 18.5, распределение вероятных цен портфеля с отрицательным коэффициентом гамма имеет более тяжелый левый хвост, чем нормальное распределение. Если предположить, что распределение вероятных цен портфеля является нормальным, оценка показателя VaR окажется слишком заниженной.
Для того чтобы вычислить показатель VaR с точностью, большей, чем та, которую обеспечивает линейная модель, необходимо выявить зависимость между коэффициентами дельта и гамма, с одной стороны, и величинами ΔР и Δxi, с другой. Рассмотрим портфель, содержащий единственный актив стоимостью S долл. Обозначим через δ и γ значения коэффициентов дельта и гамма. Как показано в приложении 15.1, формула
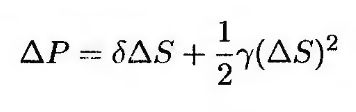
является более точной, чем формула (18.3). Полагая
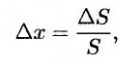
приводим это выражение к следующему виду.
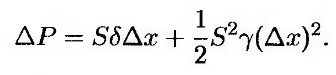 (18.6) (18.6)
Если инвестиционный портфель зависит от п рыночных показателей, причем каждая из ценных бумаг, входящих в портфель, зависит только от одного рыночного показателя, равенство (18.6) принимает вид

где Si – значение i-го рыночного показателя, a δi и γi – коэффициенты дельта и гамма портфеля по отношению к i-му рыночному показателю. Если ценные бумаги, включенные в портфель, могут зависеть от нескольких рыночных показателей, это равенство принимает более общий вид.
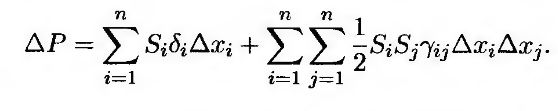
Здесь γij – это так называемый "перекрестный" коэффициент гамма, определяемый по формуле
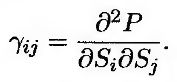
Работать с равенством (18.7) сложнее, чем с формулой (18.5). Однако с его помощью можно вычислить моменты случайной величины ΔР. Оценить перцентили распределения вероятностей случайной величины ΔР можно с помощью разложения Корниша-Фишера (Cornish-Fisher) и соответствующих моментов распределения.
|