|
Методика расчета критерия
Вернемся к общей формуле универсального критерия (1.6.1). Используя формализм теории вероятности, запишем математическое ожидание прибыли комбинации в фиксированный момент времени как:

В результате получаем критерий, который будем называть «математическое ожидание прибыли на основе логнормального распределения».
Если вместо платежной функции PF(B, S, х) подставить функцию доходности, полученную делением платежной функции на сумму инвестиций в комбинацию и на время нахождения в позиции, то прибыль превратится в доходность, а выражение 2.1.1 превратится в критерий «математическое ожидание доходности на основе логнормального распределения». Аналогично можно сформулировать и другие критерии «математического ожидания», основанные на интегрировании платежных функций по различным распределениям. Следуя идее оценки опционных комбинаций по критериям, мы соблюдаем принцип, по которому из нескольких комбинаций лучшей будет считаться та, у которой значение критерия «математическое ожидание прибыли (доходности) на основе логнормального распределения» больше.


Параметры критерия
Как следует из формулы 2.1.1, для того чтобы определить значение математического ожидания прибыли, надо представить прогноз будущей цены акции в виде функции плотности вероятности логнормального распределения. Для этого необходимо определить значения параметров используемого распределения. Поскольку для данного критерия применяется логнормальное распределение, задача сводится к вычислению двух параметров – математического ожидания цены базового актива в момент t прогноза и дисперсии нормального распределения логарифма цены акции.
Основным преимуществом опционной торговли является возможность применения маркет-нейтральных стратегий, не требующих предсказания направлений будущих изменений цены. Поэтому при определении параметра математического ожидания цены естественным будет принять его равным текущей стоимости базового актива на дату вычисления критерия. Это означает, что мы не делаем никаких предположений относительно роста или падения рынка базового актива, а рассматриваем сегодняшнюю цену как наиболее вероятную на будущую дату прогноза. Альтернативный подход состоит в придании данному параметру некоего значения, определяемого экспертным путем. Например, если фундаментальный аналитик прогнозирует рост (или падение) цены, то для расчета критерия может быть использовано значение математического ожидания, которое больше (или меньше) текущей цены акции. В первой главе говорилось о возможности построения вероятностных сценариев будущего на основе комбинирования экспертных оценок с анализом ценовых рядов. Расчет критерия «математическое ожидание прибыли» может служить типичным примером этого, если применение логнормального распределения (которое строится на основе анализа исторических ценовых рядов) совмещать с использованием экспертной оценки параметра математического ожидания цены.
Значение второго параметра – дисперсии σ2 нормального распределения логарифма цены акции – можно принять равным квадрату исторической волатильности акции. Помимо классической модели существует множество вариаций формул для расчета исторической волатильности (Garman & Klass,1980; Parkinson, 1980 и многие другие). В зависимости от выбора формулы будет изменяться и расчетная величина параметра и, соответственно, значение критерия. Мы остановимся на простейшем варианте, когда историческая волатильность HV вычисляется как среднеквадратичное отклонение логарифмов отношений последовательных цен закрытия на определенном историческом периоде:

Формула 2.1.2 представляет упрощенный вариант вычисления исторической волатильности. Однако, как показывает опыт, для практических целей ее точности вполне достаточно. Число дней N, предшествующих текущему моменту, будем называть глубиной периода для расчета исторической волатильности. Правильный выбор N является ключевым моментом в расчете данного параметра, поскольку, как следует из формулы 2.1.2 и как показывает практика, расчетное значение дисперсии крайне чувствительно к изменениям в глубине периода, используемого для вычисления исторической волатильности. Можно сказать, что истинным параметром, определяющим практическую эффективность данного критерия, является именно N. Правила определения N обычно являются тщательно оберегаемой интеллектуальной собственностью; об этом много рассуждают, но замолкают, когда речь заходит о конкретном алгоритме. Правда, однако, заключается в том, что большинство признанных гуру опционной торговли не имеют формализованных алгоритмов расчета этого параметра, а полагаются исключительно на собственный опыт. С другой стороны, не существует да и не может существовать единого, подходящего для всех случаев алгоритма. Правила определения JV меняются в зависимости от используемой опционной стратегии, горизонта прогноза, алгоритма выбора базовых активов и многих других переменных. В нашей следующей книге, в разделе, посвященном построению торговых систем, мы подробно остановимся на разработке адаптивных алгоритмов определения оптимального N для каждого представляющего практический интерес случая.
Далее мы рассмотрим пример вычисления критерия «математическое ожидание прибыли», но прежде покажем, в какой степени значение критерия зависит от величин параметров, используемых для его расчета. Воспользуемся опционной комбинацией пропорциональный длинный стрэнгл для акции APPL (полное описание комбинации приводится в примере ниже). На рис. 2.1.1 показаны расчетные значения критерия в зависимости от различных сочетаний двух параметров логнормального распределения–математического ожидания цены {Mean) и глубины периода для расчета исторической волатильности. Критерий достигает своего минимума в области значений параметра Mean близких к текущей цене акции ($94,68). Это объясняется тем, что длинный стрэнгл предполагает получение убытка, если цена не совершила большого движения И наоборот, значения параметра математического ожидания цены, которые больше или меньше текущей цены акции, приводят к росту расчетного значения критерия. Не менее очевидно влияние и второго параметра: при использования малого периода для расчета исторической волатильности значения критерия низки, увеличение этого периода сопровождается ростом критерия (рис. 2.1.]
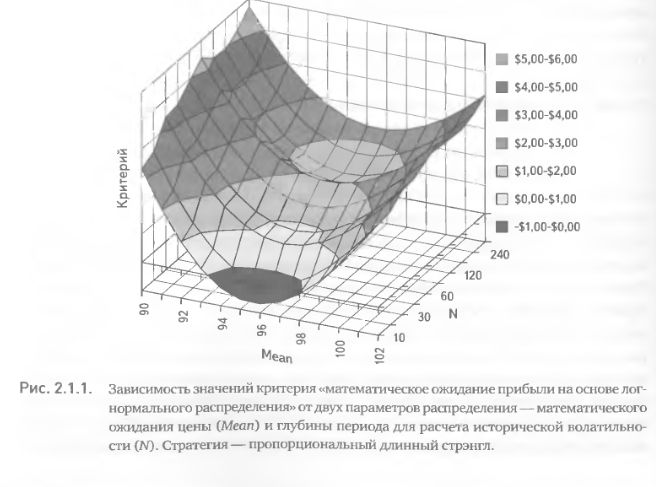
Данный пример только иллюстрирует, что значение критерия может оказаться как отрицательным, так и положительным (и даже весьма высоким) в завис мости от значений параметров, принимаемых для его расчета. Конкретные же формы такой зависимости сильно варьируют для разных стратегий, базовых активов и даже для одних и тех же сочетаний стратегия х базовый актив видоизменяются со временем. Поэтому, принимая решения о выборе значения параметров для целей реальной торговли, необходимо тщательно анализировать каждую ситуацию в контексте текущего момента времени.
Пример вычисления критерия
Определим значение критерия применительно к стратегии «пропорциональный длинный стрэнгл» для акции APPL. Пятого апреля 2007 г. цена закрытия акции составила $ 94,68; опционы с датой экспирации 21 апреля 2007 г. торговались со следующими ценами предложения: Call 90 – ask $ 5,2, Put 95 – ask $ 1,85. Рассмотрим комбинацию, составленную из двух длинных опционов пут и одного длинного опциона колл.
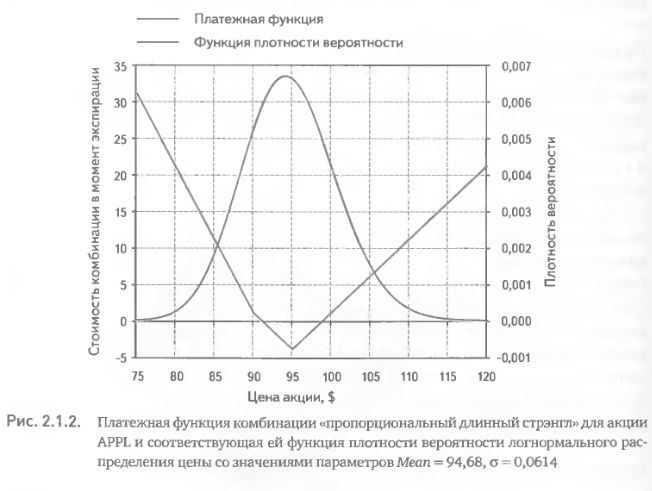
Для выбора параметров логнормального распределения предположим что математическое ожидание цены акции в момент t прогноза равно сегодняшней цене Mean = 94,68 (принцип нейтральности). Дисперсию определим с помощью формулы 2.1.2, где для расчета исторической волатильности используем 120-дневную историю цен закрытия акции (N= 120). Полученное значение исторической волатильности составило HV= 30,29%. Для вычислении q по HV необходимо ввести поправочный коэффициент, учитывающий время от настоящего момента до даты прогноза, на которую вычисляется критерий – квадратный корень отношения количества дней до искомой даты к 365. В данном случае мы заинтересованы в расчете критерия на дату экспирации (через 15 дней).

На рис. 2.1.2 изображена плотность логнормального распределения цены акции с использованием соответствующих значений параметров и платежная функция комбинации на дату экспирации с учетом покупки каждого опциона по цене предложения (стоимость комбинации составила $ 8,9). Интегрируя произведение платежной функции комбинации и плотности вероятности логнормального распределения (формула 2.1.1), получим математическое ожидание прибыли комбинации на день экспирации: MeanLogNorm = 1,6052. Что означает это число для анализа комбинации? Значение критерия оказалось положительным. Это говорит о потенциальной прибыльности комбинации. Однако использование теоретико-вероятностных конструкций при построении критерия требует правильной интерпретации результата. Полученное значение критерия вовсе не означает, что итогом инвестирования в комбинацию будет именно такой доход. Это лишь специфическая модель усреднения возможных вариантов исхода. Если бы мы могли произвести статистический эксперимент, в котором испытания происходят многократно, а исходы реализуются с частотами, определяемыми используемой функцией плотности вероятности, то средняя прибыль оказался бы равной нашему критерию. Но в реальном будущем наступит лишь один из возможных исходов. Это значит, что применение критериев, основанных на вероятностных распределениях, осмысленно только при многократном систематическом их использовании в реальной торговле.
|