|
Методика расчета критерия
В зависимости от значения будущей цены базового актива платежная функция любой комбинации может быть отрицательна, что. соответствует убытку от комбинации, или положительна, что соответствует получению прибыли. Такие длинные стрэнглы и стрэдлы неограниченно прибыльны при существенном движении цены базового актива и имеют ограниченный убыток при неизменной цене. Короткие стрэнглы и стрэдлы, наоборот, ограниченно прибыльны при малом движении цены и неограниченно убыточны при большом движении.
Поскольку различные состояния рынка не равновероятны, то возникает задача расчета вероятности получения любой отличной от нуля прибыли. Если две различные опционные комбинации имеют одинаковые или близкие показатели по некоему критерию (например, их математические ожидания прибыли равны), то более привлекательной для инвестора будет та комбинация, у которой больше вероятность оказаться в зоне прибыли.
В принятых выше обозначениях критерий «вероятность получения прибыл] по логнормальному распределению» задается следующим выражением:

Для расчета значений данного критерия используются те же два параметр что и для математического ожидания прибыли – математическое ожидание цены акции в момент t прогноза и дисперсия нормального распределения о ношения логарифмов последовательных значений цены акции.
Смысл выражения 2.1.3 легко видеть в дискретном случае, когда мы имеет конечную последовательность цен {xt, t = t1 t2,..., tn}. Вместо функции плотности распределения LogN(x) у нас будет набор вероятностей {p(xti),i = 1,2,...n реализации этих цен в будущем. Индексы i цен распадутся на два множества I+ ={i: PF(B,S, xti) > 0}, для элементов которого значение платежной функции положительно, и I = {i: PF(B,S,xc ) < 0}, для элементов которого значения платежной функции неположительны. Тогда наш критерий будет представлять о бой сумму вероятностей для элементов первого множества:
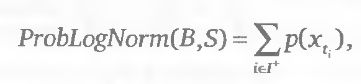


Пример вычисления критерия
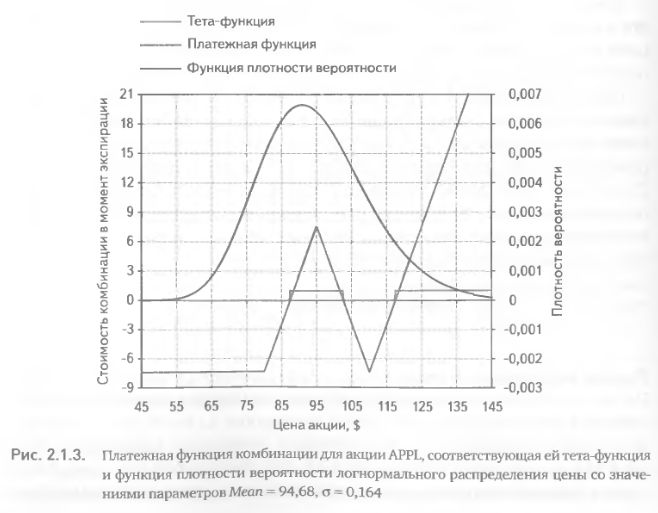
На рис. 2.1.3 показана платежная функция комбинации, состоящей из трех опционов колл на акцию AAPL с датой экспирации 21 июля 2007 г. Комбинация создана 05 апреля 2007 г. по следующим ценам: один длинный Call 80 -ask $ 17,5, два кротких Call 95 – bid $ 7,3, два длинных Call 110 – ask $ 2,2. Как и в предыдущем примере, цена акции на день создания комбинации была $94,68. В соответствии с принципом рыночной нейтральности (когда мы не пытаемся делать предсказания о направлении движения цены в будущем) значение параметра «математическое ожидание цены» было принято равным текущей цене (Mean = 94,68). Историческая волатильность на 120-дневной истории цен закрытия акции составила 30,29% (значение параметра N было выбрано таким же, как и в предыдущем примере). Число дней до экспирации равно 107. Соответственно, умножая волатильность на поправочный коэффициент, приводящий время к единицам года, получим значение второго параметра, дисперсии:
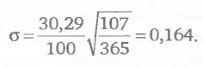
На рис. 2.1.3 изображены функция плотности вероятности логнормального распределения с принятыми нами значениями параметров, график платежной функции PF(x) комбинации, а также график интегрируемой в критерии тета-функции θ (PF(x)). Последняя равна нулю для тех цен акции, в которых платежная функция отрицательна, и единице для цен, в которых платежная функция положительна.
Численное интегрирование по формуле 2.1.3 дает значение критерия равное 0,45, т. е. по нашей оценке комбинация на момент экспирации окажется прибыльной с вероятностью 45%.
Естественно, тот же результат будет получен и для дискретного случая, если воспользоваться формулой 2.1.4. Выбор комбинаций с максимальными значениями этого критерия направлен на торговлю с минимизацией вероятности убытков. Поскольку при этом мы не оцениваем величины возможных прибылей или убытков, то этот критерий лучше использовать не как самостоятельный инструмент отбора, а в сочетании с другими критериями, прямо или косвенно выражающими возможную доходность.
|