|
Как и в случае с логнормальным распределением, критерий, прогнозирующий ожидаемое значение прибыли, полезно дополнить критерием, выражающим вероятность оказаться в зоне прибыли на интересующую нас будущую дату. Очевидно, что при примерно равных ожидаемых доходностях более привлекательной будет та комбинация, у которой выше вероятность получения прибыли при различных реализациях цены базового актива. Формально для эмпирического распределения искомый критерий задается следующим выражением:
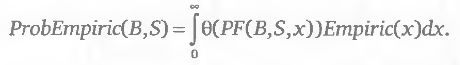
Как и в случае логнормального распределения, θ (у) представляет собой тета-функцию с аргументом у = PF(B,S,x), принимающую следующие значения: θ(у) = 1, если у > 0, и θ(у) = 0 в остальных случаях.
В нашей упрощенной вычислительной схеме этот критерий может быть рассчитан как
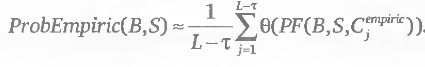


2.2.4. Упрощенный алгоритм расчета критериев, основанных на эмпирическом распределении
Для примера рассмотрим алгоритм расчета двух критериев – математического ожидания прибыли и вероятности получения прибыли на основе эмпирического распределения – по формулам 2.2.2 и 2.2.4 для стратегии «короткий стрэнгл» по акции YHOO. Построим комбинацию из одного короткого опциона колл со страйком 30, проданного по цене bid $ 0,3, и одного короткого опциона пут со страйком 27,5, проданного по цене bid $ 0,25. Цена закрытия акции на дату создания комбинации составляла $ 28,38. Дата открытия позиции – 30 мая 2007 г. Вычислим значения обоих критериев на дату экспирации опционов 15 июня 2007 г.
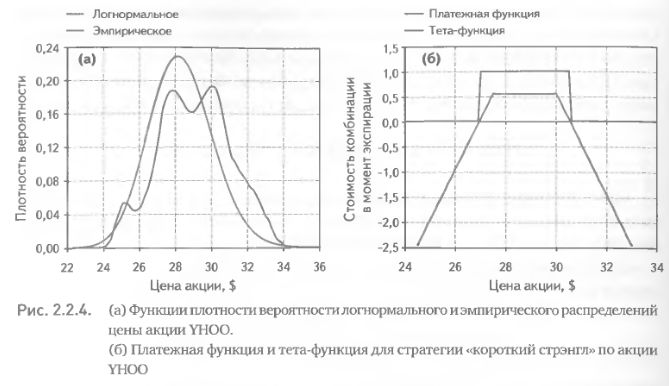
Эмпирическое распределение будем строить по горизонту истории L = 90 дней. Горизонт прогноза примем t = 16, что соответствует количеству дней, остающихся до экспирации. На рис. 2.2.4 (а) изображены кривые плотностей логнормального и эмпирического распределений. Логнормальное распределение строилось по 120-дневной исторической волатильности (28,73%). Примечательно, что в этом случае эмпирическое распределение имеет два локальных пика, причем ни один из них не достигает максимального значения плотности вероятности логнормального распределения. На рис. 2.2.4 (б) изображены платежная функция комбинации и тета-функция от нее.
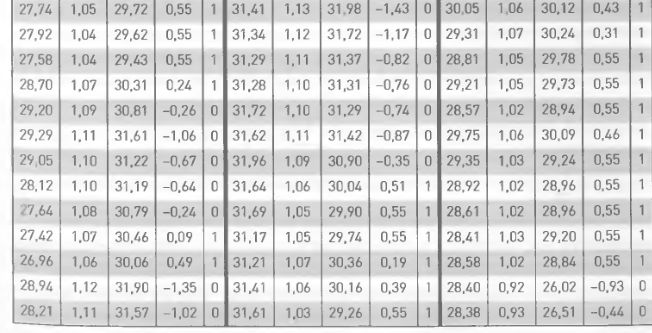
Для расчета значений критериев упорядочим 90 цен закрытия в историческом порядке (первый столбец таблицы 2.2.1). Во втором столбце таблицы приведены отношения цен закрытия pj, рассчитанные в соответствии с горизонтом прогноза (например, первое значение р. получено делением цены закрытия семнадцатого дня на цену закрытия первого дня: 26,85/26,34 = 1,02).
Третий столбец таблицы 2.2.1 содержит оценки будущей цены акции через 16 дней, полученные умножением pj на текущую цену акции в момент создания комбинации (например, первое значение Gempj получено перемножением 28,38 х 1,02 = 28,93). В четвертом столбце вычислена платежная функция PFj. рассматриваемой комбинации в точках Сempiricjна момент экспирации. В пятом столбце приведена тета-функция от PFj, принимающая значение 1 для положительных PFj и значение 0 –- для остальных.
Вычисления критериев математического ожидания прибыли Меап-Empiric(B, S) и вероятности прибыли по эмпирическому распределению ProbEmpiric(B, S) произведем по формулам 2.2.2 и 2.2.4 соответственно. Фактически значения этих критериев получаются как средние величины чисел в четвертом и пятом столбцах табл. 2.2.1: MeanEmpiric(B, S) =-0,27 и ProbEmpiric(B, S) = 0,53. Полученные значения говорят о том, что данная комбинация с точки зрения этих двух критериев вряд ли будет перспективна.
Для приведенных расчетов необходимо сделать одну важную оговорку – в этом примере значения критериев вычислялись на дату истечения опционов, но это не всегда должно быть так. Если инвестор не собирается держать позицию до экспирации, он может определить значения критериев на любую промежуточную дату. Для этого нужно ввести две поправки в приведенный выше вычислительный алгоритм. Во-первых, необходимо скорректировать горизонт прогноза таким образом, чтобы он соответствовал количеству дней от момента создания позиции до той промежуточной даты, на которую производится расчет критериев. Например, если в приведенном примере задаться целью определить значения критериев не на дату экспирации (15 июня), а на 10 июня, то горизонт прогноза составит не 16, a ll дней (соответственно изменится и расчет отношений цен закрытия рj).

Во-вторых, значения платежной функции должны быть вычислены не на экспирацию, а на желаемую дату. Здесь возникает дополнительная сложность – если расчет на экспирацию определен однозначно, то вычисление платежной функции на любую другую дату возможно только с помощью моделей. Любая модель, не исключая общепризнанную модель Блэка – Шоулза, имеет ряд недостатков, вытекающих из базовых, не всегда соответствующих реальности допущений. Поэтому расчетные значения критериев могут страдать неточностями.
|