|
В предыдущих разделах мы описали два основных типа универсальных прогнозных критериев, базирующихся на распределениях вероятностей. Показатели прогноза будущей прибыли служат критерии, выражающие математическое ожидание прибыли на основе некоего распределения, а показателем верности избежания убытка – критерии, выражающие вероятность получения прибыли на основе некоего распределения. Ниже предлагается новый универсальный, но не прогнозный критерий, косвенно совмещающий достоинство этих оценок, и обладающий дополнительными полезными свойствами.
Для любой комбинации множество значений аргумента платежной функции, т. е. совокупность возможных в будущем цен базового актива, распадается на две непересекающиеся области – зону прибыли и зону убытка. Первая область – это значения цены, при которых платежная функция положительная вторая область – значения цены, где платежная функция отрицательна. Oбозначим через PF(B, S,x) платежную функцию комбинации S базового активе Переменная х принимает всевозможные значения цены базового актива. Черезf(В,х) обозначим функцию плотности вероятности распределения цены базового актива на заданную дату. Множество всех значений цены, где платежная функция положительна, обозначим через I+ = {x: PF(B, S,x) > 0}, a MНОжество всех значений цены, где платежная функция отрицательна, – через I- = {x: PF(B, S,x) < 0}. Введем две величины, имеющие смысл интегралов платежной функции по вероятности отдельно для области прибылей Р(В, S) и области убытков L(В, S):
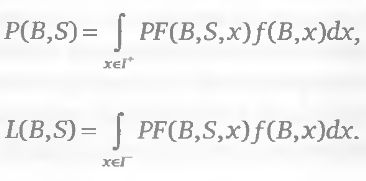


Разность Р{В, S) – L(B, S) является не чем иным, как нашим критерием «математическое ожидание прибыли по распределению/(В,х)». Значение этой величины может быть одним и тем же при разных значениях Р(В, S) и L (В, S) (например, если их изменить на одну и ту же величину).
Рассмотрим две опционные комбинации S1 и S2, у которых одинаковые математические ожидания прибыли Р(В, S1)-L(B, S1) = P(B, S2) -L(B, S2), но при этом Р(В, S1) > P(B, S2) и L(B, S1) > L(B, S2). Представим себе две торговых системы, по которым ведется систематическая торговля: первая занимает позиции с характеристиками такими же, как у комбинации S1 а вторая – как у S2 Равенство математических ожиданий прибыли означает, что в гипотетическом случае многократной торговли такими комбинациями обе торговые системы принесут одинаковую прибыль. Однако первая система сопряжена с большими величинами не только доходов, но и убытков. Грубо говоря, обе стратегии идут к одной и той же цели, но разными путями. Большие убытки, с которыми сопряжена первая торговая система, могут нанести непоправимый урон капиталу, а в случае, когда выделенный для торговли капитал ограничен, способны привести к разорению еще до того, как система сможет «отыграться». (Тонкости управления капиталом являются темой отдельного исследования и будут детально рассмотрены в следующей книге.) Аналогично, целевая доходность по первой торговой системе может оказаться недостигнутой и в том случае, если система включает в себя ограничивающий параметр максимальной просадки, останавливающий торговлю в случае достижения определенной пороговой величины. Это означает, что при одинаковом математическом ожидании прибыли комбинация S1 более рискованна, чем комбинация S2. Максимизацию прибыли с одновременной минимизацией возможных убытков, т. е. риска, можно осуществить, максимизируя следующую функцию:
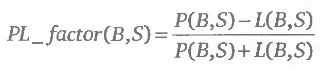
Величина PL _ factor (В, S) представляет собой критерий «соотношение ожидаемых прибыли и убытка» и принимает значения в интервале от -1 до 1. Минимальное значение – 1 означает, что комбинация убыточна при всех возможных значениях цены базового актива. Максимальное значение +1 соответствует ситуации, в которой комбинация прибыльна при всех значениях цены.
Данный критерий является, согласно нашей классификации, вариантом универсального непрогнозного критерия. Он применим к опционным стратегиям любого типа с платежными функциями произвольного вида. Фактически это целое семейство критериев, поскольку каждое распределение вероятностей f(B, x) порождает свой собственный критерий. Поэтому возможно одновременное применение нескольких критериев PL _ factor(В, S) с разными распределениями (например, с логнормальным, эмпирическим и симметричным эмпирическим) в процедуре многокритериального отбора лучших комбинаций.
Очевидным преимуществом данного критерия является его безразмерно (в отличие от математического ожидания прибыли, выражающегося в валюте базового актива) и удобный диапазон значений. В частности, использование соотношения ожидаемой прибыли и убытка позволяет сравнивать опционные комбинации по существу их структуры, независимо от того, какое количество единиц каждой из них составляет позицию. Кроме того, при использовании данного критерия благодаря его виду (формула 2.3.3) форма выражения прибыли и ее нормировка по времени не имеют значения. Напомним, что вражение в критериях «математическое ожидание прибыли» по различным распределениям слово «прибыль» могло быть заменено на «доходность», а критерии возвращались в «математическое ожидание доходности», если в подынтегральное выражение математического ожидания подставить вместо платежной функции PF(B, S,x) частное от ее деления на объем маржевых требований и время нахождения в позиции. В выражении 2.3.3 простые нормировки путем дели доходов или убытков на инвестиции и время были бы проведены как в числителе, так и в знаменателе. Таким образом, критерий PL _ factor (В, S) оказывается безразличным к указанным манипуляциям.
Поскольку изменение цены базового актива за время жизни комбинации все время меняет маржевые требования к поддержанию позиции, реалы сумма инвестиций и точное время их вложения в позицию неизвестны. Кроме того, нормировка по времени также порождает свои проблемы, так как 10 годовых, заработанных за год, не эквивалентны 100% годовых, заработанных за несколько дней. Поэтому независимость данного критерия от такого pежима нормировок делает его более надежным и универсальным для систематической оценки опционных комбинаций.
|