|
Каждый элемент первого модуля должен представлять собой простейший вариант распределения с минимальным числом параметров, то есть такой, чтобы его интерпретация была очевидна эксперту и реализовывала бы какую-то простую идею вероятностного варианта развития будущего. Остановимся подробней на базисных элементах первого модуля.
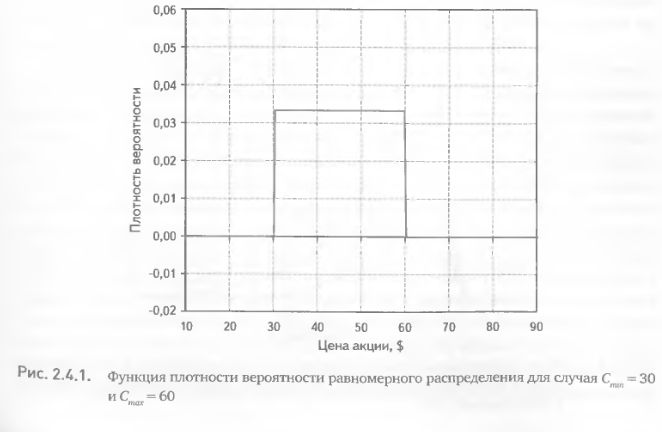
Равномерное распределение

Этот вариант прогноза означает, что с равной вероятностью цена будет принимать любые значения в диапазоне от $ 30 до $ 60 и ни при каких условиях не выйдет за его пределы. Подобные суждения эксперта могут следовать из расчета пороговых уровней переоцененности и недооцененности акции, основанного на анализе фундаментальных показателей. Подчеркнем еще раз, что мы рассматриваем не варианты окончательного прогноза, а лишь те кирпичики, из которых эксперт пытается его построить.


Логнормальное распределение
Это распределение наиболее популярно в теории опционов, математическая база его функции плотности подробно описана в разделе 2.1.1. Эксперту в качестве инструментов для манипуляций с распределением удобно пользоваться математическим ожиданием цены базового актива (напомним, что математическое ожидание – это средневзвешенное по вероятности значение цены) и его дисперсией (выраженной посредством волатильности). Эти величины доступны из многочисленных источников текущей биржевой информации, понятны и постоянно анализируются экспертами.
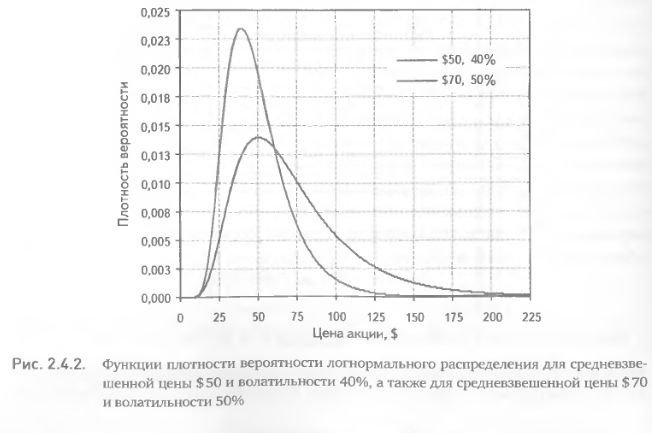
На рис. 2.4.2 изображены функции плотности вероятности логнормального распределения для средневзвешенной цены $ 50 и волатильности 40%, а также для средневзвешенной цены $ 70 и волатильности 50%. Ввиду несимметричности логнормального распределения его пик (говоря формально – мода), соответствующий наиболее вероятному значению цены, не совпадает со значением математического ожидания. На рис. 2.4.2 функция со средневзвешенной ценой $ 70 имеет наиболее вероятную цену (моду) в районе $ 50, а у функции с математическим ожиданием $ 50 пик (мода) приходится на цену $ 40. Фактически это дает эксперту вспомогательный параметр – наиболее вероятную цену – для построения своего прогноза.
Как использовать этот дополнительный, третий параметр? Ответ на этот вопрос станет понятен после того, как мы разберем общую схему работы эксперта с логнормальным распределением.
Эксперт, включающий в свой сценарий этот вариант прогноза цены, тем самым негласно предполагает, что цена базового актива представляет собой геометрическое броуновское движение с заданными значениями математического ожидания в момент будущего Т и дисперсией. Но это предположение обусловлено только математической формой логнормального распределения. На самом же деле эксперт, будучи в первую очередь фундаментальным аналитиком, рассматривает движение цены не как случайный броуновский процесс, а как направленное стремление к определенной цели, сопровождающееся псевдохаотическими колебаниями. Продолжая аналогию с броуновским движением, можно сказать, что в представлении аналитика цена является электрически заряженной броуновской частицей, движущейся не в нейтральной среде, а в электростатическом поле. В этой ситуации задача эксперта сводится к определению величины напряженности электрического поля (от этого зависит, с какой скоростью частица-цена будет двигаться к цели) и к установлению местоположения электрода, несущего противоположный заряд (от этого зависит, в какую сторону будет двигаться частица-цена). Это теоретически прямолинейное движение зашумляется непредсказуемым воздействием молекул окружающей среды, что, возвращаясь от физической метафоры к суровой финансовой практике, можно сравнить с влиянием хаотически поступающей на рынок информации. Именно так фундаментальный аналитик должен рассматривать рыночные процессы и именно такой философской концепции он должен придерживаться, используя логнормальное распределение.
Приступая к построению сценария, эксперт должен подобрать наиболее соответствующие его представлениям о будущем значения параметров логнормального распределения. Фактически он должен предсказать среднее значение будущей цены и величину ее случайного разброса. Первое не представляет большой концептуальной сложности, если эксперт уже сформировал мнение относительно фундаментальных характеристик исследуемого базового актива. Зато определение величины дисперсии представляет собой задачу, практически неразрешимую доступными эксперту средствами. Напомним, что эксперт должен основывать свои прогнозы исключительно на фундаментальном анализе, а прогноз будущей дисперсии очень сложно вывести из экономических характеристик базового актива. Есть несколько общепринятых путей решения этой проблемы. Можно спрогнозировать дисперсию на основании прошлой волатильности. Но тогда мы получим на выходе гибридные критерии, совмещающие в себе оба подхода – экспертный и базирующийся на прошлых событиях. Кроме того, можно вывести значение дисперсии из подразумеваемой волатильности опционов на данный базовый актив. Но тогда мы отказываемся от формирования собственного мнения о волатильности и полагаемся на мнение широкого рынка. Здесь мы предложим третий метод–использование наиболее вероятной цены в качестве дополнительного параметра, подменяющего собой параметр дисперсии.
В конечном итоге задача эксперта сводится к построению плотности вероятности распределения, подобной представленным на рис. 2.4.2. Такие функции полностью определяются заданием двух параметров – среднего и дисперсии. Поскольку эксперт не в состоянии определить дисперсию, он может определить значения средней и наиболее вероятной цены, а дисперсию подобрать таким образом, чтобы итоговая функция соответствовала этим двум значениям. При таком подходе мы фактически получаем значение наведенной дисперсии и готовую функцию плотности логнормального распределения. Остается решить вопрос, каким образом эксперт должен присваивать разные значения этим двум близким по смыслу величинам. Для этого мы предлагаем следующую последовательность действий. Вначале эксперт определяет первый параметр–наиболее вероятную цену. Это просто, поскольку наиболее вероятная цена полностью соответствует основному прогнозу эксперта. Далее эксперт присваивает вероятности реализации другим ценам. Для этого выбирается некий разумный (не очень большой) диапазон цен и каждой цене в диапазоне (с определенным, не очень маленьким шагом) присваивается вероятность ее реализации на момент прогноза (сумма всех присвоенных вероятностей должна равняться единице). Затем присвоенные вероятности умножаются на соответствующие им цены, полученные значения суммируются и результат делится на количество слагаемых. Это и есть значение второго параметра–средняя цена или, говоря формально, математическое ожидание цены. Далее аналитически определяется величина дисперсии, соответствующая полученным значениям двух параметров, после чего построение функции плотности не представляет сложности.
Экспоненциальное распределение
В базисе первого модуля построителя вероятностных сценариев это распределение будет полезно в случаях прогноза исходов ожидаемых корпоративных событий. Предположим, что на определенную дату назначено объявление решения Администрации США по контролю за пищевыми продуктами и лекарственными средствами (Food and Drug Administration – FDA) по медицинскому препарату, разработанному биотехнологической компанией. По мнению эксперта, если FDA одобрит коммерческое производство препарата, акция поднимется выше определенного ценового уровня. Как вариант дальнейшего развития событий эксперт предполагает, что цена будет выше этого уровня, но вероятность его превышения будет тем меньше, чем больше величина этого превышения. В случае противоположного решения–запрета на коммерциализацию препарата– цена акции резко снизится и пробьет другой ценовой уровень. В результате цена окажется ниже определенного экспертом уровня. Прогноз такого рода событий хорошо описывается совокупностью двух экспоненциальных распределений Плотность экспоненциального распределения имеет вид функции:
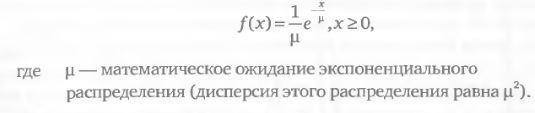
Предположим, что для описанной выше ситуации эксперт определил хи = ( в качестве уровня пробоя вверх и xd = 45 в качестве уровня пробоя вниз). Распределение для пробоя вверх задается функцией:
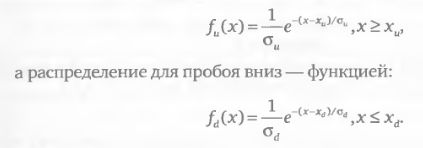
Параметры разброса σu ,σd также должны быть подобраны экспертом индивидуально для каждого случая. Значения этих параметров влияют на темг снижения вероятности для случаев прохода ценой уровней, определенных экспертом. Предположим, что эксперт придал следующие значения параметра разброса: σu = 10 для экспоненциального распределения, моделирующего пробой вверх, и σd = 5 для распределения, моделирующего пробой вниз. Тогда функции плотности вероятности для пробоя вверх ценового уровня $ 60 и для проб вниз уровня $45 будут иметь вид, показанный на рис. 2.4.3.
Три вида описанных распределений (равномерное, логнормальное и экспоненциальное) являются достаточно представительным базисным набором. Его можно дополнить и более сложными распределениями. Полезно будет так: включить в первый модуль системы построения сценариев два основных варианта эмпирического распределения и несколько распределений, моделирующих идею «тяжелых хвостов».
|