2.5.4. Отношение нормированной временной стоимости к показателю распределения абсолютных приращений цены

Структура данного критерия аналогична использованной при построении критерия «отношение IV/HV» – дробь, где в числителе находится показатель стоимости опционов, а в знаменателе – показатель изменчивости цены базового актива. Однако в этом случае оба показателя рассчитываются на основе совершенно других принципов без использования исторической и подразумеваемой волатильности. Это позволяет избежать неточностей и допущений, связанных с вычислениями обеих величин. Данный критерий обладает той же особенностью, что и отношение IV/HV– он может использоваться не столько для сравнения опционных комбинаций, сколько для анализа базовых активов с целью выбора наиболее подходящих для группы опционных стратегий – покупки или продажи волатильности. Высокие значения критерия указывают на предпочтительность для данного базового актива стратегий продажи волатильности, низкие значения – на преимущества стратегий покупки волатильности. Отдельные комбинации также могут анализироваться и сравниваться между собой посредством данного критерия, но с одним важным ограничением – сопоставимы только комбинации со строго одинаковой структурой. То есть в части анализа комбинаций критерий «отношение нормированной временной стоимости к показателю распределения абсолютных приращений цены» является абсолютно специфическим, неуниверсальным (причина этого кроется в методике расчета числителя отношения и станет понятна далее).

Начнем с числителя, выражающего меру того, насколько дорого в данный момент времени оцениваются опционы. Для этого мы пойдем самым прямым путем – рассчитаем величину временной стоимости комбинации в процентах от цены базового актива. Для того чтобы по этому показателю можно было сравнивать различные базовые активы, следует соблюдать два условия. Во-первых, все комбинации должны иметь одинаковую структуру, точнее, это должны быть стрэдлы со страйком, наиболее близким к текущей цене базового актива (можно использовать и стрэнглы, об этом речь пойдет дальше). Во-вторых, цены всех базовых активов на момент расчета критерия должны точно совпадать с ценой страйка (тогда опционная премия будет состоять исключительно из временной стоимости). Если первое условие легко выполнимо и зависит исключительно от нашей воли, то второе является идеализацией, которая никогда в реальной жизни не реализуется одновременно для большого количества базовых активов. Тем не менее, мы в состоянии аппроксимировать эту идеализацию, задавшись целью рассчитать, какова была бы стоимость опционов, составляющих комбинацию, если бы цена базового актива скачкообразно изменилась и совпала бы с ближайшим страйком. Это можно сделать, используя дельту каждого опциона. Говоря упрощенно, дельта показывает, на сколько пунктов изменится цена опциона при изменении цены базового актива на один пункт. Для того чтобы привести реальные цены опциона пут (Р_p) и опциона колл (Р_c) к гипотетическим ценам (Р'_p и Р'_c), которые образовались бы, если бы текущая цена базового актива (X) совпала с ближайшим страйком (S), нужно выполнить следующие преобразования:

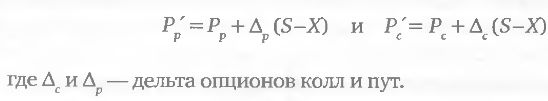
Теперь, для того чтобы выразить величину временной стоимости комбинации, нормированную на цену базового актива (которая после преобразования 2.5.6 равняется S), остается сделать один шаг:

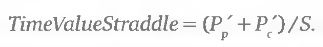
С тем, чтобы получить аналогичный показатель по стрэнглам, придется учитывать еще одну особенность. Примем следующую единую структуру стрэнглов: и для пута, и для колла будем использовать ближайшие к текущей цене базового актива (X) страйки вне денег (обозначим их соответственно S_p и S_c). При этом опционная премия комбинации будет состоять исключительно из временной стоимости. Упомянутая выше особенность состоит в том, что для разных базовых активов расстояния между соседними страйками, выраженные в процентах отХ, бывают весьма различны. Это приводит к тому, что для принятой нами структуры стрэнгла, при прочих равных условиях, большей временной стоимостью будет обладать комбинация той акции, у которой величина (S_c-S_p )/X меньше, чем у другой, сравниваемой с ней акции. И это вполне закономерно, так как страйки обоих опционов у такой акции располагаются ближе к деньгам. Чтобы нейтрализовать этот эффект и сделать все базовые активы сравнимыми по временной стоимости стрэнглов, необходимо нормировать временную стоимость на шаг страйка: (Р_p + P_c)/ (S_c-S_p ). Если полученное выражение нормировать еще и на текущую цену базового актива, получим для стрэнглов показатель, аналогичный (2.5.7):

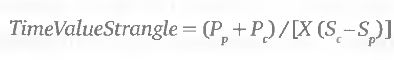
Необходимо учитывать, что нормировка временной стоимости на величину (S_c-S_p ) не полностью решает проблему сравнимости базовых активов. Причина в том, что по мере удаления текущей цены от страйка временная стоимость убывает нелинейно. В результате более дешевые базовые активы (т. е. имеющие в процентном выражении к цене более редкие страйки) будут иметь завышенную временную стоимость по сравнению с более дорогими базовыми активами. Исходя из этого, мы рекомендуем использовать формулу 2.5.8 для сравнения только тех базовых активов, цена которых не отличается более чем на 20-25%.

Выражение 2.5.7 (или 2.5.8), позволяющее сравнивать разные базовые активы по показателю стоимости их опционов, является числителем искомого отношения нормированной временной стоимости к показателю распределения абсолютных приращений цены. При этом важно помнить, что показатели, вычисляемые по формуле 2.5.7 и формуле 2.5.8, несопоставимы, так как временная стоимость стрэдла «около денег» всегда больше, чем у стрэнгла. Кроме того, эти две величины имеют разную размерность. Первая выражает величину временной стоимости в процентах от цены базового актива. Вторая, также в процентах от цены базового актива, выражает величину временной стоимости, приходящуюся на каждый доллар расстояния между страйками.

Идея показателя, стоящего в знаменателе критерия, заключается в выражении изменчивости цены базового актива без обращения к концепциям исторической волатильности и дисперсии. Эта задача может быть решена множеством способов (и еще больше способов может быть изобретено в процессе создания новых критериев). Здесь же мы рассмотрим лишь один из них. Абстрагируясь от направленности ценовых движений, попытаемся по абсолютным значениям прошлых приращений цены выразить ее изменчивость с помощью экспоненциальной функции.

Воспользовавшись методом наименьших квадратов, аппроксимируем функцию распределения F(B, х) функцией экспоненциального распределения

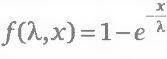
Для каждого базового актива В получится свое значение показателя λ (В). Плотность распределения экспоненциального распределения имеет вид

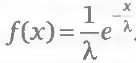
Если у двух разных акций В₁ и В ₂ получились разные значения показателя, причем λ (В₁) > λ (В₂), то у акции В₁ меньше малых приращений цены и больше больших, т. е. у распределения ее доходностеи «хвосты» толще. Такое свойство говорит о том, что цена первого базового актива более изменчива, чем цена второго.

Вычисляя отношение показателя TimeValue, рассчитанного по формуле 2.5.7 или 2.5.8, к величине λ(В), получаем значение критерия «отношение нормированной временной стоимости к показателю распределения абсолютных приращений цены».

В заключение хотелось бы отметить, что, используя данный критерий и отношение IV/HV, можно создавать дополнительные гибридные критерии. Например, можно вычислять отношения, подставляя в числитель TV, а в знаменатель Я.(В), или, наоборот, подставляя в числитель значения, рассчитываемые по формуле 2.5.7 или 2.5.8, а в знаменатель –HV.