|
Описанные выше показатели далеко не исчерпывают возможности оценки эффективности критериев. Аналитические методы, базирующиеся на близких или принципиально других подходах, постоянно развиваются и совершенствуются. Более того, различные вариации показателей эффективности могут создаваться на базе тех же принципов, которые были использованы нами в разделах 3.4.1-3.4.4.
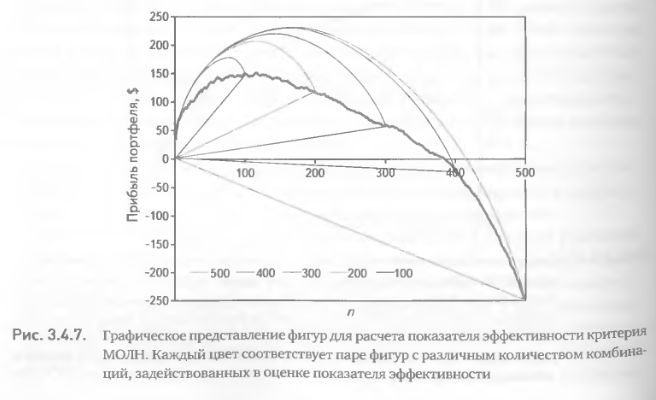
Такие вариации, выражающие в несколько ином виде прогностические качества критериев, могут быть весьма полезны для всестороннего сравнительного анализа последних. Они пригодны для использования как самостоятельные аналитические инструменты и как вспомогательные оценочные средства.


Рассмотрим несколько примеров, иллюстрирующих дополнительные способы оценки эффективности критериев (все примеры основаны на критерии МОЛН и стратегии «короткий стрэнгл/стрэдл»).
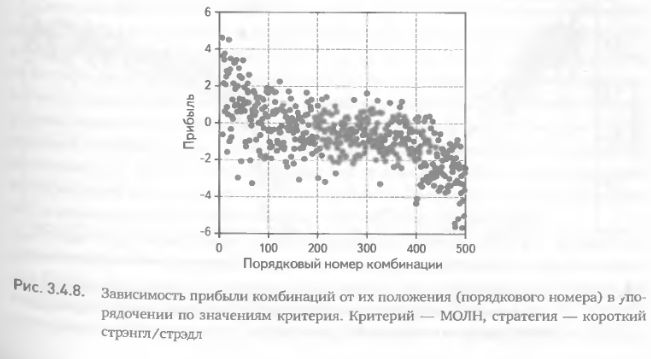
Зависимость прибыли от положения комбинаций в упорядочении. Данная методика оценки является промежуточным вариантом между индексной регрессией (раздел 3.4.2) и регрессией {критерий х прибыль} (раздел 3.4.1). Разница заключается в том, что здесь рассматривается зависимость прибыли, выраженной в долларовом эквиваленте, от значений критерия, представленных в виде индекса. В чем смысл подобной «гибридизации»? Оказывается, представление данных в таком виде вскрывает нелинейную природу зависимости прибыли от критерия (рис. 3.4.8). Увеличение номера комбинации в упорядочении по критерию от 1 до 100 сопровождается резким падением прибыли. Дальнейшее продвижение по упорядочению, вплоть до 400-го номера, практически не влияет на прибыль, зато увеличение от 400 до 500 вновь вызывает ее резкое снижение. Это свойство нелинейности, крайне важное для дифференцированной оценки эффективности критерия на различных диапазонах его значений, оставалось скрытым от нашего внимания в ходе предыдущих исследованиях.
Отклонения прогнозных значений критерия от полученной прибыли. Критерии, имеющие вид математического ожидания, прогнозируют будущую прибыль комбинаций в самой прямой и непосредственной форме.
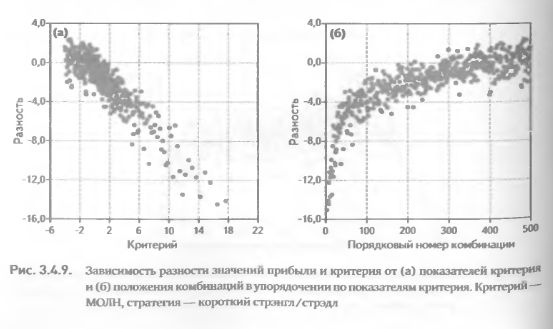
Поэтому может быть полезным рассмотреть отклонения прогнозов от их реализации, а также возможную зависимость отклонений от самих значений прогноза. Данные, представленные на рис. 3.4.9 (а), говорят о том, что в большинстве случаев прогнозные значения были завышены. Однако гораздо более удивительным оказалось наличие ярко выраженной обратной зависимости отклонений от значений 1 критерия. Чем выше были показатели критерия, тем более переоцененными оказывались комбинации. И наоборот, комбинации с низкими значениями критерия по большей части были недооценены.
Если рассмотреть зависимость отклонений от положения комбинаций в упорядочении по критерию, вырисовывается следующая картина (рис. 3.4.9(6)). Большая переоцененность комбинаций, наблюдаемая для первых номеров упорядочения, резко падает по мере увеличения порядкового номера. Однако данная зависимость нелинейна, поэтому начиная с 100-го номера темпы снижения | переоцененное™ замедляются. С 300-го номера появляются не только переоцененные, но и недооцененные комбинации. А после 400-го номера в упорядочении большинство комбинаций в среднем оказываются справедливо оцененными.
Безусловно, отклонения прибыли от прогнозных значений неизбежны. Средняя величина и разброс этих расхождений должны исследоваться статистическими методами и учитываться при практическом использовании критериев. Особенно важно не упускать из вида нелинейную зависимость отклонений от положения комбинаций в упорядочении. Как было показано в нашем примере (рис. 3.4.9), комбинации, обладающие наилучшими показателями критерия, могут быть в наибольшей степени переоценены. И хотя в большинстве своем они все-таки оказываются прибыльными, величина реально получаемой прибыли значительно ниже ожидавшейся.
Поэтому, прогнозируя будущую доходность I опционного портфеля, необходимо учитывать это свойство и стараться компенсировать его путем введения поправочных коэффициентов, корректирующих абсолютные величины прогнозных значений критериев.
Разрабатывая систему поправочных коэффициентов и методику их применения следует учитывать специфические формы зависимости отклонений от положения комбинаций в упорядочениях и от показателей критериев. В одних случаях такая зависимость может отсутствовать, в других случаях она может иметь иной вид, совершенно не похожий на тот, который был представлен на рис. 3.4.9.
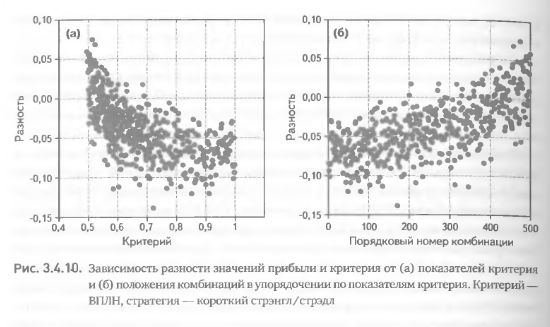
В подтверждение этого рассмотрим еще один пример. Оставаясь в рамках той же стратегии (короткий стрэнгл/стрэдл), заменим критерий, прогнозирующий величину прибыли (МОЛН), на критерий, прогнозирующий вероятность получения прибыли (ВПЛН). Как следует из рис 3.4.10, замена критерия привела к качественно новой форме зависимости. Во-первых, зависимость разностей значений прибыли и критерия от показателей критерия превратилась из линейной (рис. 3.4.9 (а)) в нелинейную (рис. 3.4.10 (а)). Во-вторых, зависимость разностей от положения комбинации в упорядочении, хотя и сохранила свою нелинейность, но изменила форму, превратившись из выпуклой (рис. 3.4.9 (б)) в вогнутую (рис. 3.4.10 (б)). И, наконец, степень двух зависимостей оказалась разной. Нет никакой необходимости в расчете коэффициентов корреляции нелинейной регрессии, чтобы убедиться в том, что мера вариации данных вокруг воображаемой линии регрессии гораздо больше для критерия ВПЛН, чем для критерия МОЛН (сравните рис. 3.4.9 и 3.4.10).
Еще более специфическими могут оказаться зависимости отклонений от значений других критериев, особенно если последние применяются для оценки опционных комбинаций в рамках других стратегий. Все особенности таких зависимостей обязательно должны приниматься во внимание при разработке и применении системы поправочных коэффициентов.
Анализ коэффициентов Шарпа. В разделе 3.4.3 мы уже использовали коэффициенты Шарпа для расчета показателя эффективности критерия на основе регрессионной зависимости коэффициентов, рассчитанных по показателям прибыли, от коэффициентов, рассчитанных по значениям критерия. Нет никаких причин ограничиваться всего одним типом подобного анализа. Коэффициент Шарпа, рассчитываемый по прибыли, является чрезвычайно важной характеристикой, несущей информацию не только о прибыльности комбинаций, но и о мере ее изменчивости. Поэтому целесообразно как можно шире использовать данный соэФфициент, что, несомненно, будет способствовать получению разносторонней и многоплановой оценки прогностических качеств критериев.
Рассмотрим два примера, иллюстрирующие возможные пути получения полнительной информации о критериях посредством анализа коэффициентов Шарпа. Для начала исследуем зависимость коэффициента от положения комбинации в упорядочении по значениям критерия (рис. 3.4.11 (а)). Как неоднократно отмечалось в предыдущих примерах, такое представление данных обнаруживает нелинейную природу зависимости.
Вначале увеличение порядкового номера комбинации сопровождается резким падением коэффициента Шарпа. После 100-го номера снижение коэффициента замедляется и лишь по достижении 400-й позиции в упорядочении возобновляется с той же силой. Выше мы уже отмечали, что нелинейность такого рода зависимостей (трудно обнаружимая в ходе применения других аналитических процедур) чрезвычайно важна для дифференцированной оценки эффективности критерия на различных диапазонах его значений.
Следующий анализ основан на изучении зависимости идеализированного упорядочения коэффициентов Шарпа от реального, полученного методом сортировки по значениям критерия. Техника данного метода достаточно проста. Сначала все комбинации сортируются по показателям критерия. На основании этой сортировки строится упорядочение коэффициентов Шарпа (рассчитанных по показателям прибыли). Затем производится вторая сортировка, на этот раз по самим значениям коэффициента Шарпа. Полученные таким образом два упорядочения коэффициентов сопоставляют между собой и исследуют их взаимозависимость (рис. 3.4.11 (б)). Каждая точка на графике регрессии соответствует определенному порядковому номеру в упорядочении по критерию (хотя сами номера на графике не фигурируют). Координатой точки по оси абсцисс является коэффициент Шарпа, полученный для данного номера. А координатой точки по оси ординат является коэффициент Шарпа, который был бы получен для данного номера в упорядочении, если бы критерий сработал идеально точно (т. е. если бы упорядочение комбинаций по критерию в точности соответствовало их упорядочению по коэффициенту Шарпа). Такой подход позволяет установить, насколько прогностические качества критерия близки к идеалу.
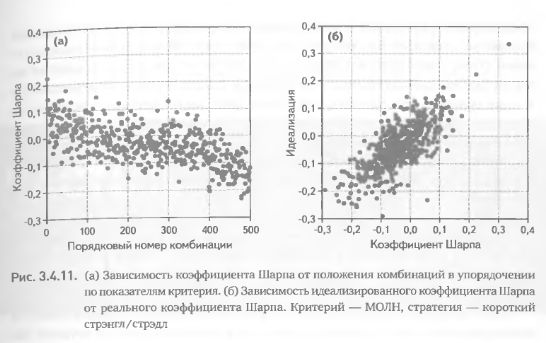
Числовым выражением показателя эффективности критерия может служить коэффициент детерминации, который в случае зависимости, представленной на рис. 3.4.11 (б), составил R 2 = 0,52.
|