|
Оценка и сравнительный анализ
Все опционные комбинации оцениваются с помощью строго формализованных критериев, разработанных специально для этих целей и выражающих торговую привлекательность и потенциальную прибыльность объектов оценки. Критерии представляют собой математические конструкции, основанные на расчетных алгоритмах разной степени сложности и включающие в себя один или несколько параметров. Поиск оптимальных значений параметров реализуется методами статистического анализа исторических временных рядов либо методом экспертной оценки. Известно, что при построении торговых систем, использующих настройку на прошлые данные, существует опасность искусственной подгонки результатов (так называемая «опасность переоптимизации»). Поэтому следует уделять самое пристальное внимание валидности статистически полученных закономерностей, применяемых для выведения оптимальных значений параметров.
Разработка критериев, позволяющих адекватно оценивать комбинации, и оптимизация их параметров являются наиважнейшими задачами, успешное решение которых во многом определяет результативность применения системного подхода. Первая часть этой книги посвящена обзору базовых принципов построения критериев и методов их параметризации. В ней же дано детальное описание некоторых критериев.
Результатом оценки по критериям является присвоение каждой комбинации числового или логического показателя, соответствующего ее качеству. Показатель качества может выражать потенциал доходности, вероятностные характеристики будущей прибыли, меру того или иного риска или любые другие свойства комбинации. Оценка может производиться по одному критерию или одновременно по многим. В последнем случае каждой комбинации присваивается столько показателей качества, сколько критериев применяется для оценки.


Далее выполняется анализ показателей оценки, который может производиться многими способами с применением специальных методик. В процессе анализа обрабатывается информация, полученная на этапе оценки, и каждая комбинация сравнивается со всеми прочими по своим показателям. Так же как и оценка, сравнение может производиться по показателям многих критериев. В итоге все доступные торговые варианты упорядочиваются по степени их предпочтительности в соответствии с показателями качества, относящимися к каждому из задействованных критериев.
Если для оценки используется несколько критериев, то в результате анализа происходит множество упорядочений. Порядковый номер элемента при упорядочении по одному показателю качества может отличаться от его номера при упорядочении по другому показателю (например, опционная комбинация может быть лучшей по ожидаемой доходности и при этом находиться на одном из последних мест по показателям риска). Все множество упорядочений может быть впоследствии сведено к единому упорядочению. Сводное упорядочение бывает как полным, так и частичным (поскольку, во-первых, некоторые элементы могут оказаться несравнимыми по показателям используемых критериев, а во-вторых, определенные комбинации могут быть лучше сравниваемых с ними вариантов по одному критерию, но хуже по другому). В случае частичного упорядочения, совокупность анализируемых элементов разбивается на группы, которые, в свою очередь, упорядочиваются как единые объекты. Методы проведения подобных процедур будут рассмотрены в главах, посвященных многокритериальному анализу.
Предварительный отбор
Следующим шагом является использование результатов сравнительного анализа для выбора комбинаций, обладающих наилучшими показателями качества. Другими словами, задача сводится к предварительному отбору тех вариантов, которые в определенной мере превосходят все прочие. Это наиболее важная и ответственная процедура, поскольку ее результатом является предварительное решение о том, какие комбинации войдут в портфель, а какие будут отвергнуты. Хотя на следующем этапе количество выбранных комбинаций может сократиться вследствие процедур фильтрации, окончательный отбор производится не по критериям оценки, а по другим соображениям, и, следовательно, высока вероятность попадания ошибочно отобранных элементов в окончательный портфель. А варианты, ошибочно отклоненные при выполнении процедуры предварительного отбора, теряются безвозвратно.
Для того чтобы определить комбинации, являющиеся кандидатами на включение в окончательный портфель, следует руководствоваться тремя соображениями. Во-первых, количество выбранных элементов должно быть достаточным для поддержания диверсификации портфеля не ниже минимально допустимого уровня. Как и в классической теории портфеля, это позволит минимизировать специфические риски, связанные с отдельными базовыми активами. Во-вторых, показатели критериев для отобранных комбинаций должны превышать аналогичные показатели для отвергнутых комбинаций. Определение оптимального порогового значения величины превышения требует разработки специальных методик. И в-третъих, при отборе следует ориентироваться не только на относительное превосходство лучших комбинаций над худшими (определяемое путем сравнения соответствующих значений критериев). Важную роль играют также и абсолютные значения критериев. Например, при сравнении двух комбинаций, имеющих значения критерия «математическое ожидание прибыли» -$ 2 и -$ 10, первая, несомненно, лучше второй и может быть выбрана как имеющая более высокое значение критерия. Однако абсолютное значение критерия у первой комбинации недостаточно велико (указывает на отрицательную величину ожидаемой прибыли), а следовательно, первая комбинация, так же как и вторая, не может быть отобрана в качестве кандидатуры на включение в портфель.
Ситуация осложняется тем, что вышеперечисленные принципы отбора могут на практике противоречить друг другу. Так, руководствуясь пороговой величиной (второе соображение) и абсолютным значением критериев (третье соображение), инвестор будет стремиться сократить количество отбираемых комбинаций. Следуя же принципу диверсификации портфеля (первое соображение), инвестор, напротив, постарается увеличить число прошедших отбор комбинаций. В итоге процедура предварительного отбора приведет к формированию портфеля, являющегося компромиссом между тремя принципами.
Теперь перейдем к рассмотрению основного вопроса: каким образом на базе анализа показателей критериев провести черту, отделяющую потенциально хорошие комбинации от плохих. Начнем с простейшей ситуации, когда имеется множество комбинаций, состоящее из N элементов, упорядоченных по показателям единственного критерия. Необходимо из этого множества выбрать N' лучших комбинаций. Для решения этой задачи следует создать функцию полезности, аргументом которой будет количество выбираемых элементов (т. е. максимальный порядковый номер выбранного элемента в упорядочении), а значением функции будет показатель, отражающий меру полезности выбора именно такого количества комбинаций. Примером функции полезности может быть зависимость между средней прибылью (максимальной просадкой, коэффициентом Шарпа, другим показателем, отражающим меру соответствия запросам инвестора) и количеством отобранных комбинаций (N').
Большинство функций полезности невозможно вычислить аналитическими методами, поскольку не существует формул, задающих связь между значением и аргументом такой функции. Поэтому значения функций полезности выводятся эмпирическим путем из прошлых ценовых данных. Для этого используются различные статистические методы.
Задача существенно усложняется, если приходится использовать не одну, а несколько функций полезности. В этом случае придется сводить множество функций к одной результирующей. Такое сведение возможно благодаря тому, что все функции имеют общий аргумент. Основное требование, предъявляемое к способу сведения функций полезности, – однозначность результата. Иначе говоря, результирующая функция должна быть унимодальной, т. е. иметь единственный явно выраженный максимум в области оптимального количества отбираемых комбинаций. В этом случае можно считать, что сводная функция полезности позволяет отобрать такое количество комбинаций из первых номеров упорядоченного по критерию множества, которое наилучшим образом соответствует требованиям инвестора. Среди множества способов сведения нескольких функций к одной самыми распространенными являются мультипликативная и аддитивная свертки. Мы предлагаем другой способ сведения – минимаксную свертку (см. главу 5), которая во многих случаях дает гораздо более надежные и однозначные результаты.
Дальнейшее усложнение задачи выбора происходит, когда приходится опираться на значения не одного, а многих критериев одновременно. В такой ситуации можно воспользоваться методами многокритериального анализа (рассматриваются в третьей части данной книги).
Порядок действий, понятие «матрицы» и ее редукции
На первом этапе реализации концепции системного подхода оценивается и анализируется огромное количество элементов. Так как в любой момент времени на каждый базовый актив i торгуется mi. опционов, то количество комбинаций, которые можно построить для одного базового актива, задается величиной Зmi.(здесь мы для простоты считаем, что один опцион может не входить в комбинацию вообще или входить в нее только в единичном числе в «коротком» или «длинном» варианте). Соответственно, для n базовых активов число возможных опционных комбинаций вычисляется по формуле:
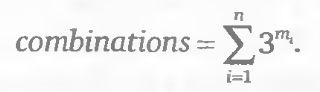
Если инвестор работает с 1000 базовых активов,, на каждый из которых активно торгуется в среднем 20 разных опционов, то для выполнения процедур первого этапа необходимо обработать более 300 млрд элементов. И это при допущении, что все опционы входят в комбинации в соотношениях, удовлетворяющих указанному выше упрощению. Если же допустить вполне реальную возможность неравных соотношений для разных опционов в пределах одной комбинации, то получится воистину астрономическое число обрабатываемых элементов.
Это число настолько велико, что вычисления, необходимые для выполнения предварительного отбора, не под силу даже самому совершенному компьютеру. Поэтому необходимо вводить алгоритмы, генерирующие не любые произвольные комбинации, а только такие, которые представляются потенциально пригодными в рамках создаваемой торговой системы (совокупность таких комбинаций будем в дальнейшем называть исходным множеством).
Прежде всего инвестор должен определить набор опционных стратегий, с которыми он собирается работать, и строить комбинации только в рамках этих стратегий. Это существенно сократит количество элементов, попадающих в исходное множество. После этого для каждой стратегии необходимо задать набор разумных ограничений. Например, для комбинаций, соответствующих стратегии «короткий стрэнгл», ограничения могут выглядеть следующим образом: разница между страйками колла и пута меньше 25% от стоимости базового актива; соотношение коллов и путов находится в интервале 0,8-1,2; и для коллов, и для путов не допускается использование более одного страйка. Такие ограничения вполне легитимны и никоим образом не сужают потенциал инвестора по использованию многообразия возможностей опционного рынка. В то же время эти меры настолько сократят количество элементов исходного множества, что оно станет доступно для обработки с помощью современной вычислительной техники.
Дальнейшее облегчение и оптимизация вычислений достигается путем проведения серии последовательных отборов вместо одновременного осуществления процедур первого этапа для всего исходного множества. В каждом отборе на ограниченном подмножестве исходного множества решается отдельная локальная задача. Это не только позволяет сократить количество вычислений, но и дает возможность выполнять их параллельно на нескольких компьютерах. Такое последовательное выполнение процедур предварительного отбора представляется более логичным и методологически обоснованным.
Мы предлагаем следующий порядок действий. До инициирования процедур первого этапа инвестор формирует массив потенциально приемлемых базовых активов и набор опционных стратегий, по которым может вестись торговля. Затем определяется алгоритм генерирования опционных комбинаций. После этого все исходное множество доступных для торговли комбинаций представляется в виде трехмерного пространства {базовые активы х стратегии х комбинации}, на котором в дальнейшем производятся процедуры оценки, анализа и предварительного отбора.
Чтобы наглядно представить подобное пространство, предположим, что алгоритм построения опционных комбинаций позволяет создавать в рамках каждой стратегии только одну комбинацию для каждого базового актива. Тогда пространство исходного множества превращается из трехмерного в двумерное Такое двумерное пространство можно представить в виде таблицы, строками которой являются базовые активы, а столбцами – стратегии. В каждой ячейке таблицы находится опционная комбинация, соответствующая конкретному б; бавому активу и определенной стратегии. В дальнейшем мы будем называть такие таблицы матрицами. Количество элементов двумерной матрицы определяетсяроизведением количества базовых активов на количество стратегий.
Если использовать алгоритм генерирования комбинаций, создающий в рамках ратегии не одну, а множество комбинаций для каждого базового актив; то в каждой ячейке таблицы (двумерной матрицы) будет находиться не единичная комбинация, а множество комбинаций, относящихся к одной стратегии и одному базовому активу. В этом случае двумерная матрица превраается в трехмерную, элементы которой представляют собой исходное множество.
Процедура предварительного отбора представляет собой редукцию трех мерной матрицы. Мы предлагаем выполнять ее путем трех последовательны: операций.
Первая операция является выбором одной или нескольких лучших комбинаийдля каждого сочетания базового актива и стратегии. Предположим, что исходное множество состоит из 30000 элементов (1000 базовых активов, 5 стратгий и 6 комбинаций на каждый базовый актив в рамках одной стратегии. Если для каждого сочетания {базовый актив х стратегия} выбирается единственный элемент из шести возможных, то исходное множество сокращается с 30 000 до 5000 элементов, а трехмерная матрица превращается в двумерную Методам реализации этой операции посвящена глава 4 данной книги.
Вторая операция – это выбор для каждого базового актива одной лучшей стратегии. В предыдущем примере эта операция ведет к дальнейшему сокращению исходного множества. Если выбирается единственная стратегия, то исходное множество сокращается до 1000 комбинаций. В результате происходит окончательная редукция матрицы, поскольку для каждого базового актива выбирается только одна стратегия (иначе говоря, каждой стратегии соответствует уникальный набор базовых активов). Поэтому оставшуюся 1000 комбинаций уже нельзя представить в виде цельной таблицы, не содержащей пробелов В главе 5 мы подробно рассмотрим особенности данной операции.
Третья операция направлена на выбор лучших вариантов из уникального НЕ бора базовых активов, соответствующих каждой стратегии. Если предположить что при проведении этой операции отбирается в среднем 10% из всех оставшихся комбинаций, (хотя в реальности эта величина может быть очень изменчивой) то остается всего 100 комбинаций, прошедших предварительный отбор. Методы осуществления этой операции разбираются в главе 6.
Такая последовательность действий – лишь одна из возможных схем peaлизации процедуры предварительного отбора. Возможны и другие, более сложные способы редукции матрицы исходного множества. Например, вместо одной комбинации для каждого сочетания {базовый актив х стратегия} можно выбирать любое их количество. Аналогично для каждого базового актива вместо одной стратегии можно выбрать несколько. В данной книге мы ограничимся рассмотрением описанной выше схемы, поскольку даже в этом, относительно простом случае существует множество специфических особенностей и масса вариантов действий, часть из которых будет исследована ниже.
|