|
Для начала рассмотрим 347 коэффициентов эффективности критерия, полученных при сравнении стратегии «длинный стрэдл» со стратегией «короткий стрэдл». Распределение значений коэффициента по частоте встречаемости представлено на рис. 5.2.3. Наиболее часто встречающееся значение к (67 случаев) лежало в диапазоне 1-1,05; на втором месте по частоте был диапазон 1,05-1,1 (54 случая); и лишь на третьем месте по частоте встречаемости коэффициента (43 случая) оказался диапазон, находящийся ниже единицы, 0,95-1 (рис. 5.2.3). Накопленная частота встречаемости различных значений к представлена на рис. 5.2.3 линией. Мы видим, что лишь в 10% случаев к был меньше 0,9 и менее чем в 40% случаев оказался меньше единицы. Среднее значение коэффициента эффективности критерия для данной пары стратегий оказалось равно .029. Достаточно ли такое отличие от 1, чтобы считать доказанной способ-ость критерия отбирать акции, для которых стратегия «длинный стрэдл» лучше, чем «короткий стрэдл»? Ответ на этот вопрос зависит от результатов статистического анализа.
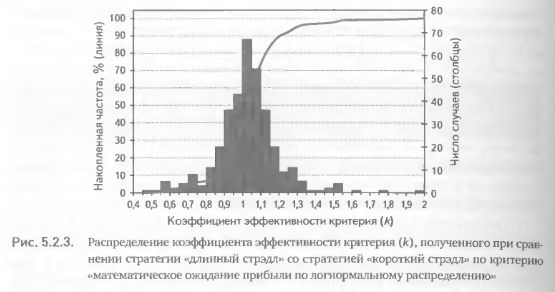


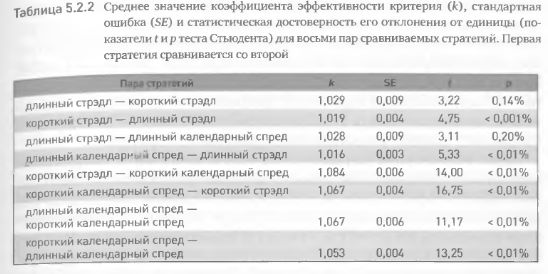
Тест Стьюдента показал, что к = 1,029 статистически достоверно отличается от единицы. Для всех прочих пар сравниваемых стратегий мы также получили средние значения коэффициента эффективности критерия несколько выше единицы (табл. 5.2.2). Однако величина этого превышения была очень незначительна. Тем не менее из таблицы видно, что изменчивость этого коэффициента, выраженная через стандартную ошибку (отношение стандартного отклонения к квадратному корню из числа наблюдений), также очень мала. Это говорит о том, что, несмотря на небольшое превышение коэффициента над единицей, оно достаточно персистентно. Более того, тест Стьюдента показал, что для всех пар стратегий отличие к от единицы статистически достоверно. Величина р в табл. 5.2.2 показывает вероятность того, что вывод о достоверности отличия к от 1 ошибочен. Как видим, вероятность ошибочных выводов в данном исследовании крайне мала и не превышает доли процента.
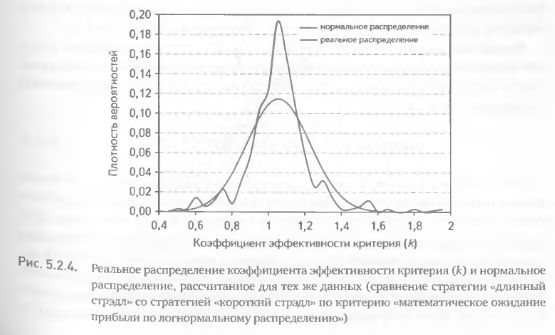
Тем не менее нельзя полностью полагаться на результаты теста Стьюдента или другого подобного статистического теста (например F-теста) ввиду того, что эти тесты подразумевают нормальное распределение исследуемой величины. Распределение же коэффициента эффективности критерия далеко от нормального. На рис. 5.2.4 показано распределение к, полученное при сравнении стратегии «длинный стрэдл» со стратегией «короткий стрэдл», и нормальное распределение для этих же данных. Расхождение двух распределений очевидно – реальное распределение имеет в центральной части высокий и узкий пик, в то время как нормальное распределение имеет гораздо более плавную форму. В реальности это означает, что значение коэффициента к в диапазоне от 1 до 1,1 встречается гораздо чаще, чем это предполагается плотностью вероятности нормального распределения. С другой стороны, значения к, несколько меньшие единицы и несколько большие 1,1, встречаются реже, чем при нормальном распределении.
Ненормальность распределения к обусловлена его природой. Нормальное распределение имеет убывающую, но ненулевую вероятность реализации очень больших и очень малых значений переменной. Другими словами, «хвосты» нормального распределения неограниченны. В отличие от этого, к по определению не может быть меньше нуля, т. е. его распределение ограничено слева. Справа также имеется ограничение, обусловленное тем, что в каждом конкретном случае величина к не может быть больше некоего максимально достижимого значения (ниже мы приведем формулу для расчета этого значения в каждом конкретном случае).
Максимально достижимые значения к ограничивают распределение справа. Итак, имеется достаточно аргументов в пользу того, что распределение интересующего нас параметра не нормально. Это означает, что мы не можем полностью полагаться на результаты общепринятых статистических тестов, базирующихся на нормальном распределении вероятностей. Следовательно, необходимо искать дополнительные подтверждения достоверности превышения единицы коэффициентом эффективности критерия.
Одним из возможных направлений статистического анализа, не требующих нормальности распределения, являются непараметрические тесты. Они позволяют сравнить частоту случаев, когда к был меньше единицы, с частотой случаев, когда к был больше единицы. В нашем примере значение к < 1 наблюдалось в 134 случаях (38,6% от 347), к >1 – в 213 случаях (61,4%). Используя тест для разницы между двумя пропорциями, основанный на биномиальном распределении, можно показать, что указанное соотношение отличается от равновероятного отношения 1:1 на очень высоком статистически значимом уровне. Вероятность того, что значение к > 1 было случайным в 61,4% случаев, составляет всего 0,003%. Можно порекомендовать также тест хи-квадрат, характеризующий отличие экспериментально полученных частот от любых ожидаемых. В качестве ожидаемых частот можно использовать половину суммарного количества наблюдений, проверяя таким образом гипотезу о том, что значения к > 1 и к < 1 встречаются с одинаковой частотой, а любые наблюдаемые отклонения от этих частот получаются случайно (в статистике это называется нулевой гипотезой). В нашем примере тест хи-квадрат показал, что нулевая гипотеза может быть отвергнута с вероятностью совершить ошибку менее 0,02% (x2 = 16,7). Таким образом, оба непараметрических теста показали статистическую достоверность того факта, что к > 1 не случайно был получен чаще, чем к < 1.
В качестве дополнительного, третьего способа оценки способности критерия указывать на предпочтительную опционную стратегию можно порекомендовать регрессионный анализ. Для этого формулу 5.2.1 нужно преобразовать следующим образом:
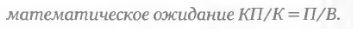
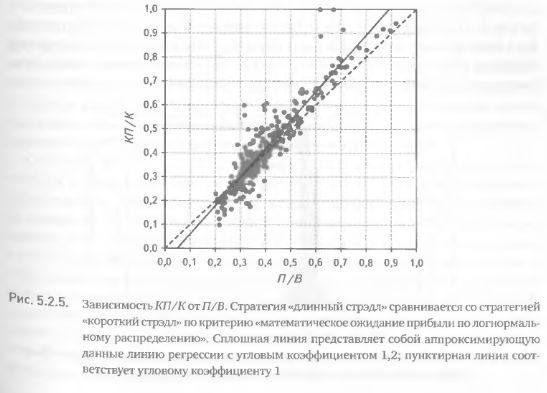
Это говорит о том, что в случае, если критерий «не работает», доля комбинаций, бывших лучшими по критерию и оказавшихся лучшими по прибыли, от числа комбинаций, бывших лучшими по критерию {КП/К), будет равна доле комбинаций, оказавшихся лучшими по прибыли, от общего числа использованных для анализа комбинаций (П/В). В обратном же случае, если критерий «работает», получим КП/К > П/В. Чтобы проверить это неравенство с использованием всех 347 значений к, необходимо рассмотреть регрессионную зависимость КП/К от П/В. Если коэффициент наклона линии регрессии окажется больше единицы, можно заключить, что КП/К действительно больше П/В, и значит, критерий позволяет выбирать лучшую стратегию.
Проведем такой регрессионный анализ для выбранной нами пары стратегий. Результат его представлен на рис. 5.2.5. Угловой коэффициент линии регрессии оказался равным 1,2 и его отличие от единицы статистически значимо (t = 7,19, p < 1%)- Таким образом, регрессионный анализ также подтвердил эффективность критерия в распознании лучших стратегий.
Следовательно, можно сделать вывод, что из трех использованных статистических тестов все подтвердили устойчивую прогнозную силу критерия в решении поставленной задачи. Мы доказали, что предложенная нами методология рангового анализа действительно позволяет решать задачу количественной оценки способности критерия распознавать более выигрышные опционные стратегии. Кроме того, мы убедились, что критерий «математическое ожидание прибыли по логнормальному распределению» позволяет выбрать комбинации, для которых стратегия «длинный стрэдл» лучше стратегии «короткий стрэдл». Однако здесь нужно сделать важную оговорку: другие критерии при анализе других пар стратегий могут дать совершенно иные результаты.
В общем случае можно порекомендовать следующее эмпирическое правило: если из трех описанных выше методик две показывают статистически значимую прогнозную силу критерия, можно полагаться на достоверность этих выводов и использовать отобранные таким путем критерии и стратегии для практической работы.
В приведенном выше примере все три использованные методики показали положительный результат, но так бывает далеко не во всех случаях. Чтобы убедиться в этом, рассмотрим еще один пример – исследуем эффективность того же критерия при отборе комбинаций, для которых стратегия «короткий стрэдл» предпочтительней стратегии «длинный стрэдл».
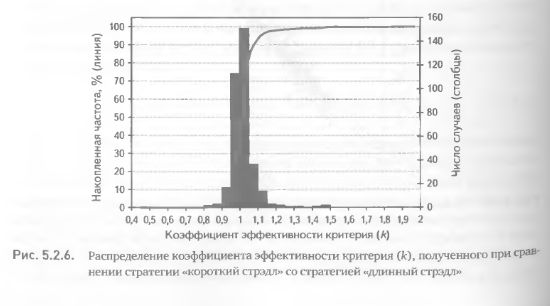
Среднее значение коэффициента эффективности критерия составило 1,019 т. е. несколько ниже, чем в предыдущем примере, но его отличие от единицы было статистически значимо на очень высоком уровне (гораздо более высоком, чем в первом примере, см. табл. 5.2.2). Распределение значений к демонстрирует убедительное смещение в сторону значений, превышающих единицу (рис. 5.2.6). Лишь менее чем в 5% случаев к был меньше 0,9 и менее чем в 40% случаев его величина оказалась меньше единицы.
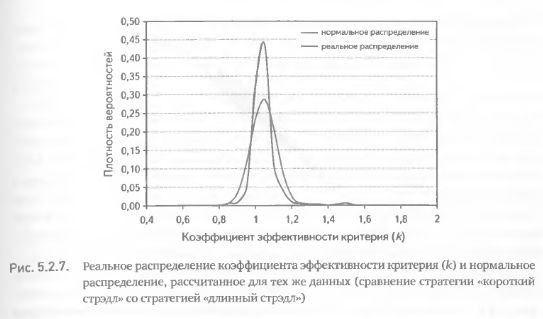
Однако распределение к в этом случае оказалось еще более отличным от нормального, чем в предыдущем примере (рис. 5.2.7). Область значений, близких к среднему (т. е. несколько больше единицы) существенно доминирует над соответствующей областью нормального распределения. Соседние же области умеренных отклонений от среднего, напротив, представлены гораздо более редкими данными, чем предполагается при нормальном распределении (рис. 5.2.7). Это вновь заставляет усомниться в доказательстве превышения к над единицей с помощью только параметрического теста, основанного на нормальности распределения.
Перейдем ко второму методу анализа – использованию непараметрических тестов. В этом примере к < 1 был в 135 случаях (39,6% от 347), соответственно к > 1 был в 212 случаях (61,4% случаев, показатель, очень близкий к первому примеру). Тест для разницы между двумя пропорциями, основанный на биномиальном распределении, показал, что полученное соотношение статистически значимо отличается от 1:1 (р = 0,004%).
Тест хи-квадрат так же подтвердил статистическую достоверность отличия реальных частот от распределения, ожидаемого в случае неэффективности критерия в решении задачи выбора стратегий (х2 = 16,7, р = 0,037%). Таким образом, непараметрические тесты, так же как и в первом примере, подтвердили достоверность того, что не случайно значение к > 1 получалось чаще, чем к < 1.
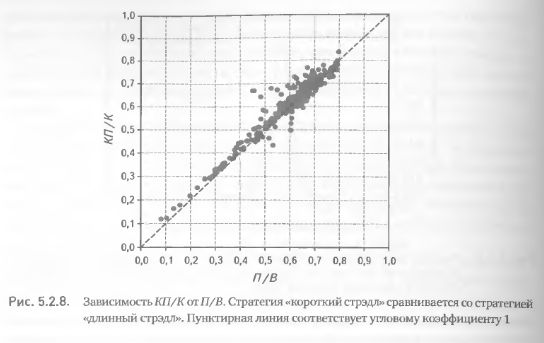
В заключение проведем исследование по третьей методике – регрессионный анализ. Вот здесь-то нас и ожидает сюрприз. Дело в том, что угловой коэффициент линии регрессии практически равен единице. Это хорошо видно на графике зависимости КП/К от Я/В, где все точки равномерно распределяются вдоль линии с наклоном 1 (рис. 5.2.8). Это означает, что в отличие от первого примера данная методика не подтвердила статистическую значимость эффективности критерия при отборе комбинаций, для которых стратегия «короткий стрэдл» лучше стратегии «длинный стрэдл».
Суммируя результаты анализа по двум примерам с использованием трех методик, можно сказать, что в одном из случаев все три методики подтвердили эффективность использованного критерия в решении поставленной задачи. Во втором же случае такое подтверждение было получено только по двум методикам, в то время как третья показала негативный результат. Тем не менее и второй пример укладывается в предложенное нами эмпирическое правило – Двух подтверждений из трех достаточно для вывода о приемлемости критерия.
месте с тем необходимо подчеркнуть, что тот же критерий при оценке любой фугой пары стратегий может оказаться непригодным. Поэтому мы настояно Рекомендуем не использовать в практической торговле ни один из вновь разработанных критериев, предварительно не исследовав его по всем трем
методикам применительно к каждой паре потенциальных стратегий.
|