5.4. Синтетический подход к анализу эффективности критериев

Итак, мы представили две методики анализа эффективности критерия – одну общепринятую и применяемую повсеместно для решения самых разных задач и другую, разработанную нами специально для решения конкретной задачи и учитывающую недостатки и неопределенности стандартного подхода.

Первая методика, базирующаяся на расчете средней прибыли и коэффициента Шарпа, вполне адекватна при работе с финансовыми инструментами, имеющими линейные платежные функции, однако она имеет целый ряд недостатков при оценке сложных опционных конструкций, платежная функция которых нелинейна. В частности, при сравнении двух стратегий по показателю средней прибыли одна из стратегий может иметь безграничный потенциал прибыли, в то время как другая – ограниченный. В такой ситуации первая стратегия может быть убыточной для большинства комбинаций, но иметь большую прибыль по нескольким из них. В результате средняя прибыль оказывается положительной и даже может оказаться весьма высокой. Вторая же стратегия с ограниченным потенциалом прибыли может показать небольшую прибыль по всем или подавляющему числу комбинаций, но ее средняя прибыль оказывается ниже, чем по первой стратегии. Корректен ли вывод, что первая стратегия предпочтительнее второй? Положительный ответ на этот вопрос дать весьма затруднительно, поскольку, хотя первая стратегия и имеет более высокую среднюю прибыль, получена она была лишь за счет нескольких, возможно случайных, выбросов. Частично (но лишь частично!) здесь может помочь применение коэффициента Шарпа, отражающего изменчивость прибыли. Однако однозначного ответа мы все равно не получим, так как по показателю прибыли первая стратегия будет предпочтительнее второй, а по коэффициенту Шарпа– наоборот, вторая окажется лучше первой. Это лишь одна проблема, создаваемая разницей в потенциалах прибыли. Потенциал убытков зачастую также разнится у сравниваемых стратегий, что создает дополнительные сложности. Если прибавить сюда осложнения, вызванные различиями в расчете маржевых требований, приводящих к возникновению разной базы для вычисления прибыльности сравниваемых стратегий, то становится очевидно, что традиционная методика имеет целый ряд существенных недостатков и нуждается в дополнительной системе оценки.

В качестве альтернативы нами разработана методика рангового анализа. Принципиальное ее отличие от общепринятой состоит в том, что она оперирует частотами возникновения или невозникновения определенных событий, абстрагируясь от абсолютных величин отдельных исходов. Использование частоты срабатываний критерия независимо от того, насколько сильно прибыль превзошла наши ожидания или разочаровала нас, позволяет избавиться от нежелательных эффектов влияния единичных экстремальных выбросов на результирующие выводы. Кроме того, и это очень важно, ранговый анализ, в отличие от общепринятого, позволяет не просто оценить возможность или невозможность получения прибыли, а показывает, насколько полно реализован потенциал получения прибыли. Достигается это за счет выведения коэффициента, являющегося косвенной мерой того, насколько полученная прибыль близка к максимально достижимому значению. Вместе с тем ранговый анализ также имеет ряд особенностей, в силу которых его эксклюзивное применение не позволяет составить полную картину о возможностях критерия при выборе опционных стратегий.

В силу вышесказанного оптимальным решением представляется комбинированное использование обеих методик как дополняющих друг друга. При этом не следует забывать, что эти подходы основываются на обработке различной информации по одним и тем же операциям, поскольку оценивают одни и те же комбинации, построенные по тем же базовым активам, их множествам и подмножествам. Вследствие этого логично предположить, что и результаты двух методик должны оказаться в некоторой степени близкими. Чтобы выяснить степень близости и расхождения этих двух подходов, надо проанализировать меру взаимозависимости их показателей.

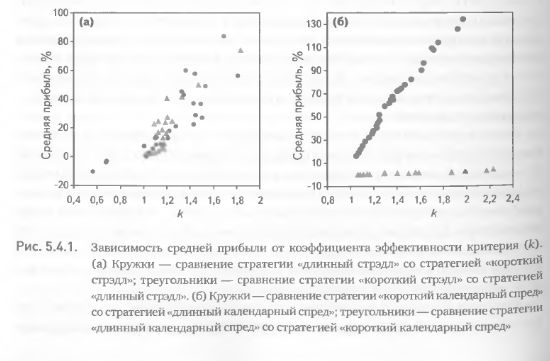
Для этого исследуем корреляцию между коэффициентом эффективности критерия и средней прибылью для двух пар стратегий, рассмотренных подробно в предыдущих примерах. Построим графики зависимости двух показателей координаты точек на которых будут представлять собой средние значения прибыли и к для определенной величины порога. Как и ожидалась, при сравнении коротких и длинных стрэдлов наблюдается прямая зависимость средней прибыли и к (рис. 5.4.1 (а)). Разброс точек, как при сравнении первой стратегии со второй, так и при сравнении второй с первой, довольно широк. Это свидетельствует о том, что, несмотря на корреляцию показателей, они могут дополнять друг друга в отражении прогностических свойств критерия. Отсюда следует, что при оценке эффективности критерия для целей торговли разумно руководствоваться значениями обоих показателей.

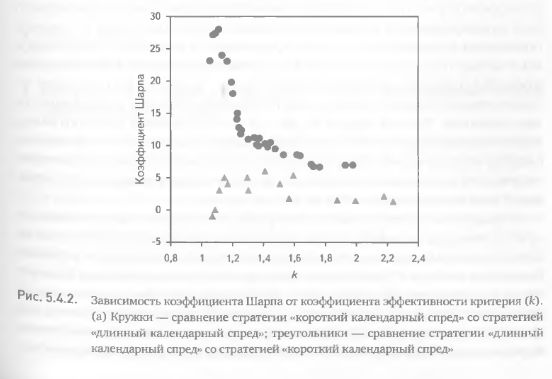
При сравнении коротких и длинных календарных спредов прослеживается гораздо более сильная взаимозависимость между прибылью и коэффициентом эффективности критерия (как при сравнении первой стратегии со второй, так и при сравнении второй с первой). В этом случае коэффициенты корреляции близки к единице и практически все точки лежат на прямых линиях (рис. 5.4.1 (б)). Столь сильная корреляция указывает на то, что информация, содержащаяся в одном из показателей, дублируется во втором. На первый взгляд это должно привести к заключению, что использование двух методик оценки не имеет смысла и для практических целей можно ограничиться лишь одной из них. Но не будем торопиться с выводами. Вспомним, что важной характеристикой прибыли является не только ее среднее значение, но и степень изменчивости, отражающая меру риска и стабильности получаемых результатов. Рассмотрим для этой же пары стратегий зависимость между к и коэффициентом Шарпа, сочетающим в себе и величину, и меру изменчивости прибыли (отношение средней прибыли к стандартной ошибке). Анализируя связь между двумя методами оценки, получаем картину, противоположную предыдущей – явно выраженную обратную зависимость между исследуемыми величинами в одном случае и полное отсутствие зависимости – в другом (рис. 5.4.2). Это означает, что и для данной пары стратегий также целесообразно применение обеих методик оценки эффективности критерия.

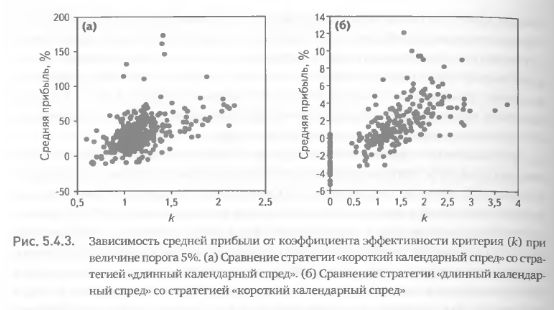
Дополнительное представление о мере и форме взаимозависимости двух показателей эффективности критерия дает изучение их корреляции в некой конкретной точке на шкале порога. Остановимся на примере сравнения коротких и длинных календарных спредов при величине порога 5%. В данном случае координаты точек на графиках будут представлять собой значения прибыли и к, рассчитанные для определенной даты. При сравнении длинного календарного спреда с коротким, равно как и при обратном сравнении, была получена прямая зависимость двух показателей, однако корреляция в обоих случаях весьма далека от абсолютной (рис. 5.4.3). Довольно широкий разброс точек на рис. 5.4.3 (а) и 5.4.3 (б) является еще одним подтверждением того, что информация об эффективности критерия, заключающаяся в двух показателях, лишь частично пересекается и в достаточно большой степени является комплементарной, а не дублирующейся.

Можно дать строгое количественное выражение мере совпадения информации, содержащейся в двух показателях эффективности критерия. В статистике коэффициент детерминации (квадрат коэффициента корреляции) трактуется как доля изменчивости зависимой переменной, объясняемая изменчивостью независимой переменной. В рассматриваемой ситуации невозможно выделить зависимую и независимую переменную, поскольку ни одна из них не влияет на другую, а корреляция между ними объясняется наличием целого ряда дополнительных факторов, оказывающих влияние на обе исследуемые величины. Эти факторы по-разному влияют на каждую из переменных, вследствие чего их корреляция не является полной. Несмотря на это, нам кажется корректным интерпретировать квадрат коэффициента корреляции между k и средней прибылью как долю информации об эффективности критерия, содержащейся как в одном, так и в другом показателе. Соответственно, доля новой, недублирующейся информации, попадающей в систему оценки за счет введения дополнительного показателя, определяется разностью единицы и коэффициента детерминации. Так, для данных на рис. 5.4.3 при сравнении длинного календарного спреда с коротким r² = 0,48, при обратном сравнении r² = 0,25. Отсюда следует, что доля новой информации о прогностических свойствах критерия, получаемой благодаря использованию не одного, а двух показателей, составляет 52% в первом случае и 75% во втором случае.

Подводя итог, можно сказать, что в рамках системного подхода к анализу прогностических способностей критерия при выборе опционных стратегий целесообразно комбинированное, синтетическое применение показателей обеих оценочных методик. Совместное использование разных показателей является особенно продуктивным, когда на их основе формируются функции полезности для оценки оптимальных значений параметров. В следующем разделе мы займемся построением рабочей модели для установления оптимальной величины порога на основе одновременного использования пяти функций полезности.