|
В этой главе мы неоднократно возвращались к понятию порога, демонстрируя, что его значение принципиально влияет как на величину потенциальной прибыли, так и на эффективность критерия при выборе лучших опционных комбинаций. Зададимся целью решить следующую практическую задачу: определить оптимальное значение порога, удовлетворяющее условию максимизации комплекса показателей полезности. Пороговое значение, при котором достигается максимум того или иного показателя полезности, может сильно варьировать вплоть до того, что максимум по одному из показателей может совпадать с минимумом по другому. В связи с этим задача сводится к построению интеграционной модели приведения многих показателей полезности к единой функции, имеющей, по возможности, единственное и явно выраженное максимальное значение, что позволяет недвусмысленно определить величину оптимального порога.


Для построения оптимизационной модели используем пять функций полезности, каждая из которых представляет собой эмпирическую зависимость определенного показателя от диапазона значений порога. В модель будут включены пять функции полезности, основанные на следующих показателях:
-коэффициент эффективности критерия (к);
-отношение k/k max (выражает меру приближения реально полученного к к своему максимально достижимому значению);
-средняя прибыль;
-коэффициент Шарпа для средней прибыли;
-количество комбинаций, попадающих в множество К (выражает степень диверсификации портфеля).
Каждая из этих функций имеет свой масштаб принимаемых значений. Поэтому нашим первым шагом будет приведение значений всех пяти функций полезности к единому масштабу величин. Для этого из каждого значения вычтем минимальные значения и разделим на разность между максимальным и минимальным значением. В результате такой нормировки значения всех пяти функций будут лежать в интервале от нуля до единицы. Следующий шаг– сведение пяти функций полезности к одной методом свертки. Воспользуемся двумя общепринятыми методами свертки – аддитивной и мультипликативной. когда каждому значению оптимизируемого параметра соответствует постоянное количество значений функций полезности (в нашем случае оно постоянно и равно 5), аддитивная свертка эквивалентна среднему арифметическому, мультипликативная – среднему геометрическому (подробнее о свертках и их разновидностях рассказано в главе 7). Дополнительно мы предложим третий разработанный нами вид свертки – произведение минимального и максимального из значений, принимаемых пятью функциями полезности для каждой величины порога (назовем ее минимаксной сверткой). Как будет показано далее, именно такой вид свертки дает наилучший и наиболее однозначный результат.
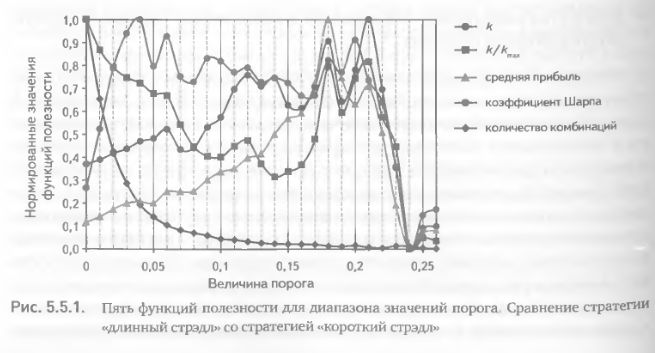
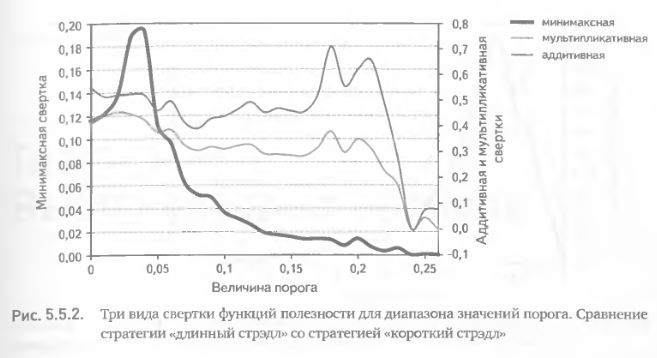
Начнем построение описанной выше модели со сравнения стратегии «длинный стрэдл» со стратегией «короткий стрэдл». Для наглядности построим в единой системе координат графики эмпирических нормированных значений всех пяти функций полезности. С первого взгляда видно, что максимумы и минимумы разных функций приходятся на разные значения порога, формы этих функций также весьма различны (рис. 5.5.1). Очевидно, что визуально невозможно определить компромиссное значение порога, удовлетворяющее условию одновременной максимизации всех пяти функций полезности. Для этого применим три вида свертки и сравним их результаты. Аддитивная и мультипликативная свертки ломаной, «неправильной» формы не дают однозначного результата, поскольку имеют несколько близких по величине пиков для разных значений порога (рис. 5.5.2). Предлагаемая нами минимаксная свертка имеет вид унимодальной функции, однозначно указывающей на единственную оптимальную величину порога – 4% (рис. 5.5.2).
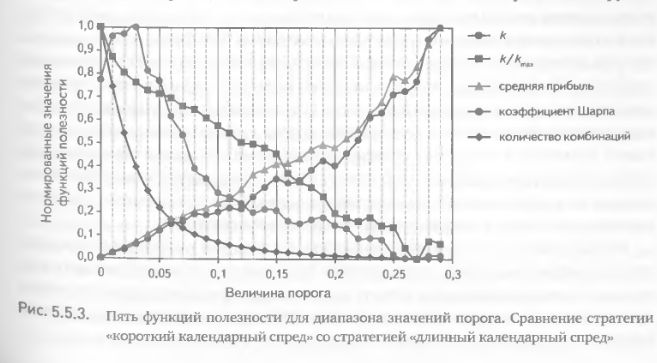
Теперь рассмотрим другой пример (сравнение стратегии «короткий календарный спред» со стратегией «длинный календарный спред»), в котором функции полезности имеют совершенно другую форму. В этом случае три функции монотонно убывают по мере увеличения порога, в то время как две другие – возрастают (рис. 5.5.3). И вновь визуальный анализ рис. 5.5.3 не дает возможности определить величину порога, удовлетворяющую наиболее достижимой максимизации всех функций полезности. Для решения этой задачи обратимся к сверткам.
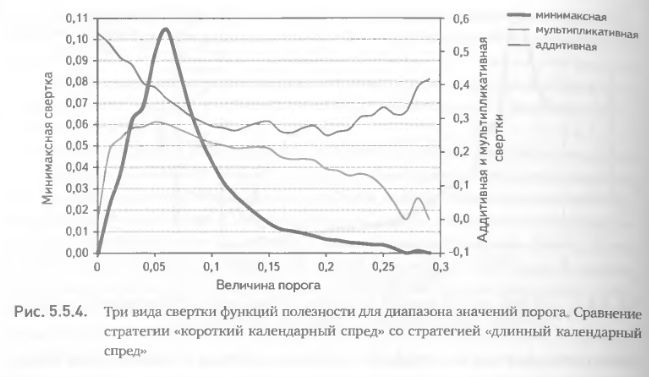
Аддитивная свертка в данном случае совершенно бесполезна, поскольку имеет вогнутую форму, достигая максимумов на двух разных концах диапазона значений порога (рис. 5.5.4). Мультипликативная свертка также не представляет большого интереса ввиду того, что ее функция не имеет явно выраженного пика, а представляет собой широкое плато в довольно обширном диапазоне пороговых значений. В противоположность этому минимаксная свертка вновь имеет унимодальный вид и дает «красивый», легко интерпретируемый результат (рис. 5.5.4). Оптимальная величина порога составила 6%.
Описанная здесь модель определения оптимального порога может быть с успехом применена для любых других сочетаний стратегий и других критериев. Более того, принцип ее построения может быть адаптирован для других ситуаций, требующих оптимизации некоего параметра по набору функций полезности.
Предложенная нами специально для этих целей минимаксная свертка является чрезвычайно полезным инструментом, позволяющим решать многокритериальные задачи выбора в сложных условиях, когда другие методы не дают приемлемого результата.
|