|
Рассмотрим процедуру анализа эффективности критериев при решении задачи выбора базовых активов на примере стратегии «короткий стрэнгл/стрэдл». Предположим, что выбран следующий алгоритм построения комбинаций. Для каждого базового актива выбирается единственная комбинация (стрэнгл или стрэдл), обладающая наиболее симметричным графиком платежной функции относительно текущей цены базового актива (выбор производится по критерию «степень симметричности», описанному в разделе 4.4.1). Комбинации создаются из контрактов, относящихся к ближайшей дате экспирации, с равным соотношением коллов и путов.
В главе 3, посвященной оценке эффективности критериев, мы обосновали необходимость использования 100-дневного временного периода (названного диапазоном усреднения) в целях достижения приемлемого уровня достоверности оценочных процедур. Здесь мы воспользуемся той же методикой, взяв в качестве отправной точки 10 сентября 2007 г. Выберем 500 акций США по признаку наибольшей ликвидности их опционов. На каждую из 100 дат построим для каждой акции одну комбинацию, соответствующую стратегии «короткий стрэнгл/стрэдл». Полученное таким образом множество комбинаций можно представить в виде таблицы, состоящей из 500 строк (по количеству акции) и 100 столбцов (по количеству дат). Элементами таблицы являются 50000 комбинаций, каждую из которых будем характеризовать двумя показателями – значением критерия на дату оценки и величиной прибыли на соответствующую дату экспирации. Значения критерия и прибыли будем выражать в процентах от маржевых требований.


Если в пределах каждого столбца этой таблицы упорядочить комбинации по значениям критерия, то средние арифметические показателей n-й строки будут представлять собой среднее значение критерия и прибыли для комбинаций, находящихся на n-м месте в упорядочении. Всего таких упорядочений будет 100 (по числу дат в диапазоне усреднения), а средние значения будут рассчитываться по выборке из 100 элементов. Помимо средних арифметических можно рассчитать также показатель, выражающий меру изменчивости прибыли в пределах каждой строки (т. е. для каждого порядкового номера в упорядочении комбинаций по критерию). Показатель изменчивости выразим в виде стандартной ошибки, рассчитываемой как отношение стандартного отклонения к квадратному корню из количества элементов выборки (в данном случае – из 100).
Выполнив указанные процедуры, получим средние значения и стандартные ошибки величин критерия и прибыли для комбинаций, находящихся на первых местах упорядочений, на вторых местах и так далее, вплоть до 500-х мест. Для анализа эффективности каждого критерия необходимо повторить все описанные выше процедуры, упорядочивая комбинации по его значениям.
Для оценки эффективности критериев при выборе базовых активов воспользуемся следующей методикой. Предположим, что инвестор располагает определенной фиксированной суммой. Этот капитал может быть инвестирован в единственный базовый актив (точнее, в единственную комбинацию, построенную по одному базовому активу). В таком случае прибыль от инвестиции равна прибыли комбинации, находящейся на первом месте в упорядочении. Если вся сумма инвестируется в n базовых активов, это означает, что капитал распределяется равномерно между n комбинациями, находящимися на n первых местах в упорядочении. При таком распределении капитала выраженная в процентах прибыль инвестиции равна среднему арифметическому из процентных прибылей n комбинаций.
Рассмотрим зависимость прибыльности такой инвестиции от количества базовых активов, используемых для распределения капитала между относящимися к ним комбинациями. Если критерий действительно способен эффективно выбирать лучшие базовые активы, то упорядочение комбинаций по значениям критерия должно соответствовать их упорядочению по прибыльности. Это означает, что комбинации, расположенные на первых местах упорядочения, Должны быть в среднем более прибыльными, чем комбинации, находящиеся на следующих за ними местах. В этом случае прибыльность инвестиции будет тем меньшей, чем большее количество базовых активов задействуется для распределения капитала.
Расчеты, выполненные по описанной выше методике, подтверждают ярко выраженную отрицательную зависимость прибыльности инвестиции от количества базовых активов (рис. 6.2.1). Этот вывод справедлив для всех без исключения критериев. Интересна также форма зависимости. В большинстве случаев прибыль падает экспоненциально с ростом числа базовых активов.
Это означает, что включение в портфель каждой дополнительной комбинации, расположенной в упорядочении на более низкой позиции и, следовательно обладающей более низкими показателями критерия, приводит к резкому падению прибыли. Распределение капитала между комбинациями, соответствующими базовым активам, занимающим первые 200 мест в упорядочении, вызывает падение прибыли до нулевой отметки, а включение в портфель базовых активов расположенных в упорядочении еще ниже, приводит к убыткам.
Зависимости, представленные на рис. 6.2.1, свидетельствуют о том, что в той или иной степени все критерии успешно справляются с решением задачи выбора базовых активов. Однако из-за экспоненциальной формы большинства зависимостей различия между отдельными критериями невидимы. Кроме того на рисунке невозможно представить меру изменчивости прибыли. Чтобы проиллюстрировать индивидуальные особенности критериев и охарактеризовать изменчивость результатов, представим данные, приведенные на рис. 6.2.1, в несколько ином виде.
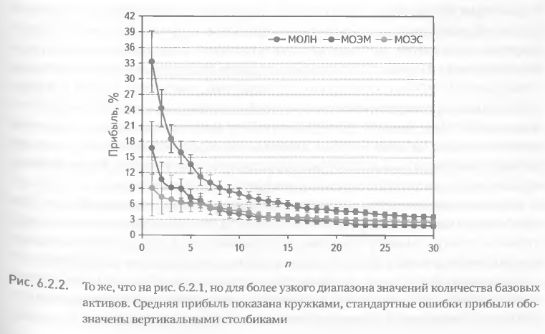
Сократим диапазон количества базовых активов, используемых для распределения капитала между соответствующими им комбинациями, с 500 до 30. Это позволит сделать данные на рисунке более читаемыми. Кроме того, для каждого количества базовых активов приведем значения не только средней прибыли, но и стандартной ошибки. Это позволит получить представление о мере изменчивости результатов. Проиллюстрируем интересующие нас зависимости на примере трех критериев, прогнозирующих ожидаемую прибыль на основе логнормального распределения (МОЛН), эмпирического распределения (МОЭМ) и симметризованного эмпирического распределения (МОЭС).

Темпы падения прибыли оказались наибольшими для критерия МОЛН, в этом случае график зависимости имеет ярко выраженную экспоненциальную форму (рис. 6.2.2). Упорядочение базовых активов по критерию МОЭМ приводит к более плавному снижению прибыли. И, наконец, в случае критерия МОЭС падение прибыли скорее линейно, чем экспоненциально (рис. 6.2.2). Это говорит о том, что упорядочение базовых активов по критерию МОЛН наилучшим образом соответствовало их упорядочению по реализовавшейся прибыли. Более всех «ошибается» в определении будущей прибыли МОЭС, а промежуточное место занимает критерий МОЭМ. Следовательно, можно заключить, что в данном случае из трех критериев наиболее эффективен МОЛН.
Независимо от критерия стандартные ошибки имеют наибольшее значение для малых количеств базовых активов, используемых при распределении капитала (рис. 6.2.2). Это говорит о большой изменчивости прибыли среди первых номеров упорядочения комбинаций по значениям критерия. Хотя средняя прибыль комбинаций, находящихся на более низких позициях в упорядочениях, ниже, ее величина более стабильна. Следовательно, несмотря на максимальную среднюю прибыль базовых активов, расположенных на первом месте в упорядочении, в портфель необходимо включать больше чем один базовый актив. Это способствует снижению волатильности и, следовательно, риска портфеля. Ниже, разрабатывая модель оптимизации количества базовых активов, мы опираемся на показатель, учитывающий не только среднюю прибыль, но и стандартную ошибку (таким показателем является коэффициент Шарпа).
Представленные выше примеры свидетельствуют о способности критериев успешно решать задачу выбора наилучших базовых активов. Этот вывод справедлив в общем виде, хотя эффективность различных критериев неоднородна.
Вместе с тем приведенные данные не могут в полной мере характеризовать прогностические качества критериев. Причина кроется в ограничении проведенных исследований всего одной стратегией и небольшим временным периодом (100 дней). Поэтому следует расширить временные горизонты и протестировать эффективность критериев на нескольких разнонаправленных стратегиях.
|