|
В главе 5 мы уже говорили о способах сведения множества функций полезности к единой результирующей. Напомним, что основное требование, предъявляемое к методике сведения,–однозначность результата. В данном случае это означает, что результирующая функция должна иметь единственный явно выраженный максимум в области оптимального значения количества отбираемых базовых активов (т.е. должна быть унимодальной). В дополнение к общеизвестным методикам сведения эмпирических функций (таким, как мультипликативная и аддитивная свертки) мы предложили другой способ – минимаксную свертку, которая во многих случаях дает более надежные и однозначные результаты. Поскольку при сведении двух функций полезности минимаксная свертка эквивалентна мультипликативной, ею мы и воспользуемся.
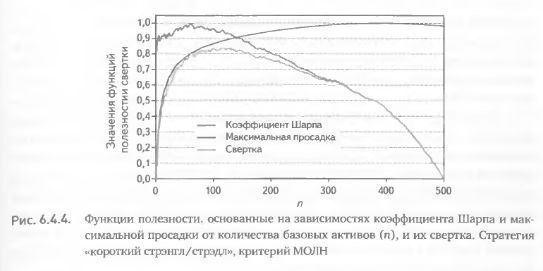


Значения функций полезности, основанных на коэффициенте Шарпа и на максимальной просадке, измеряются в различных единицах, представляют собой разные величины и, следовательно, имеют разный масштаб значений. Поэтому необходимо привести полученные эмпирическим путем значения обеих функций полезности к единому масштабу величин. Для этого найдем минимальные и максимальные значения каждой функции. Затем из каждого значения вычтем минимум, а результат разделим на разность между максимумом и минимумом. После такой нормировки значения обеих функций будут лежать в интервале от нуля до единицы. Кроме того, поскольку оптимизация по функции полезности, основанной на максимальной просадке, требует нахождения ее минимума, возникает необходимость в еще одном преобразовании – следует вычесть ее нормированные значения из единицы.
В результате всех преобразований получаем две функции полезности, приведенные к единому масштабу величин. Оптимизация интересующего нас параметра требует максимизации обеих функций. Мультипликативная свертка двух функций достигается произведением их значений. Результирующая функция имеет диапазон значений в пределах от О до 1. На рис. 6.4.4. приведен пример двух функций полезности и их свертки для стратегии «короткий стрэнгл/стрэдл» и критерия МОЛН. Мультипликативная свертка имеет достаточно гладкую унимодальную форму и достигает своего максимума при n = 116. Это позволяет легко интерпретировать полученный результат, говорящий о том, что с высокой степенью достоверности оптимальным решением является распределение капитала между 110-120 базовыми активами.
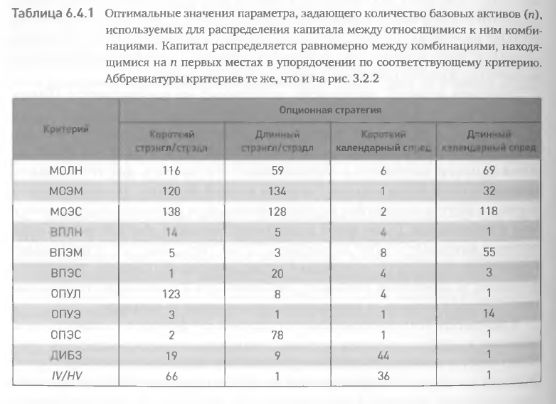
Теперь с помощью той же методики определим оптимальные значения параметра в случае применения других критериев и других опционных стратегий Повторим все описанные выше процедуры для 11 критериев и 4 стратегий. Результаты приведены в табл. 6.4.1. Очевидно, что оптимум исследуемого параметра весьма изменчив и варьирует как между критериями в пределах определенной стратегии, так и между стратегиями в пределах определенного критерия. Сложно установить какие-либо бесспорные закономерности в распределении оптимальных значений. Тем не менее, с определенными оговорками, можно заключить, что при использовании критериев, прогнозирующих вероятности получения прибыли, оптимальным является распределение капитала между меньшим числом базовых активов, чем при использовании критериев, прогнозирующих ожидаемые прибыли. Кроме того, можно утверждать, что для календарных спредов в целом оптимальным является меньшее количество базовых активов, чем для стрэнглов/стрэдлов.
|