|
Начнем с простейшего алгоритма построения множества Парето, прямо следующего из определения. Напомним, что во множество Парето входят те элементы, которые не доминируют друг над другом, но при этом доминируют над вариантами, не входящими в это множество. Простейший алгоритм заключается в поочередном выборе элементов исходного множества и сравнении выбранного элемента с каждым из оставшихся. Если найдется элемент доминирующий над выбранным, то мы переходим к следующему варианту, поскольку выбранный элемент заведомо не принадлежит к множеству Парето. Если же ни один элемент множества не доминирует над выбранным, то выбранный вариант помещается во множество Парето. Затем выбирается следующий элемент, и так до тех пор, пока не будут проверены все варианты выборки.


Этот легко программируемый и интуитивно понятный алгоритм обладает существенным недостатком. Поскольку для каждого элемента выборки требуется сравнение со всеми вариантами, то общее число сравнений пропорционально квадрату объема выборки. При этом следует помнить, что сравнение требует времени, пропорционального числу используемых при сравнении критериев. Как показывает наш опыт, при использовании двух критериев и числе элементов выборки порядка 1000 время работы алгоритма вполне приемлемо, но при дальнейшем росте многократно увеличивается.
Более эффективный, но более сложный в реализации алгоритм использует предварительное упорядочение элементов согласно значениям критериев. Представим, что мы оцениваем некое исходное множество по двум критериям. На первом этапе упорядочим элементы выборки по убыванию одного из критериев. Первый по порядку элемент имеет наибольшее значение этого критерия и в силу этого факта уже принадлежит к множеству Парето – никакой иной элемент выборки не может доминировать над ним. Двигаясь по списку элементов выборки, упорядоченному по убыванию, сравниваем их с найденным членом множества Парето и, если элемент оказывается доминируемым, удаляем его из выборки. Таким образом, после первого прохода у нас будет один элемент, заведомо принадлежащий множеству Парето, и совокупность кандидатов на включение в это множество. Мы еще не можем утверждать, что они все являются недоминируемыми, поскольку знаем только, что их не доминирует уже включенный во множество элемент. Однако мы уже способны назвать еще один элемент, который можно включить во множество Парето. Это первый из них по порядку, ведь в силу того, что элементы упорядочены по значению критерия, его не доминируют все остальные элементы выборки, а также уже включенный в множество Парето элемент. Переносим его в множество Парето, а оставшиеся элементы сравниваем с ним, удаляя доминируемые. Это второй шаг. Повторяем шаги, пока не исчерпаем исходный список элементов. К этому моменту формирование множества Парето будет завершено. Применяемые ныне алгоритмы сортировки требуют числа операций, пропорционального N log(N), где N–число сортируемых элементов.
Рассмотрим описанную последовательность действий на примере, ограничившись исходным множеством из 30 опционных комбинаций, построенных для стратегии «короткий стрэдл/стрэнгл». Для каждой из 30 акций была выбрана единственная комбинация – стрэнгл или стрэдл – по принципу наибольшей симметричности. Этот принцип реализуется путем максимизации показателя
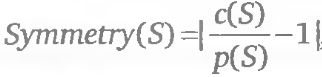
где c(S) и p(S) – премии опционов колл и пут, соответствующие страйку S.
Количество продаваемых опционов колл и пут в каждой комбинации были равными. Каждая комбинация была оценена по двум критериями (математическое ожидание прибыли на основе логнормального распределения и отношение IV/HV). Оценка проводилась по данным на 1 марта 2007 г., использовались только опционы с ближайшей датой истечения. Результаты приведены в табл. 7.2.1.
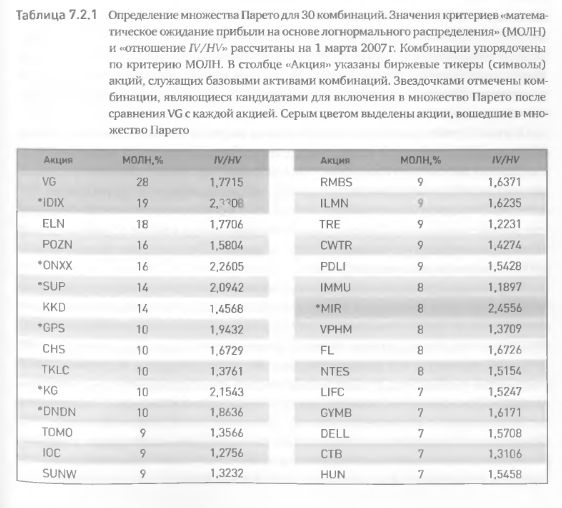
Упорядочение по первому критерию определяет первый элемент множества Парето – VG (табл. 7.2.1). Все остальные варианты сравниваются с ним по второму критерию, и элементы, которые он доминирует, удаляются из набора. В результате остаются только семь комбинаций, которые могут претендовать на включение в множество Парето: IDIX, ONXX, SUP, GPS, KG, DNDN, MIR (отмечены звездочками в табл. 7.2.1). Вторым элементом, помещаемым в множество Парето, является IDIX. После сравнения с ним оставшихся элементов остается только MIR, оказывающийся третьим и последним членом множества Парето.
Таким образом, вместо 870 операций, которые потребовались бы в случае сравнения каждого элемента со всеми прочими, нам понадобилось только 36. По мере возрастания объема исходного множества преимущество этого алгоритма возрастает еще больше.
|