19.2. Модель экспоненциально взвешенного скользящего среднего

Модель экспоненциально взвешенного скользящего среднего (EWMA) представляет собой частный случай модели (19.4), в которой веса α_i с течением времени убывают со скоростью степенной функции. Конкретнее говоря, α_i+1 = λα_i, где λ – константа, лежащая в диапазоне от нуля до единицы.

Оказывается, взвешенная схема позволяет упростить формулу для вычисления волатильности.

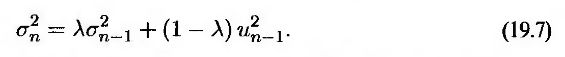
Таким образом, в этой модели оценка σ_n волатильности рыночного показателя в n-й день (измеренного в конце (n – 1)-го дня) вычисляется с помощью оценки σ_n-1 волатильности рыночного показателя в (п – 1)-й день (измеренного в конце (п – 2)-го дня) и величины u_{n-1 (последнего относительного изменения рыночного показателя).}

Для того чтобы продемонстрировать, почему формула (19.7) соответствует весам, убывающим со скоростью степенной функции с основанием А, подставим в нее величину σ²_n-1. Тогда

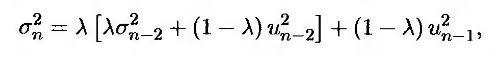
т.е.

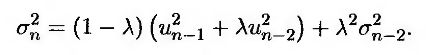
Аналогично, подставляя в формулу (19.7) выражение для параметра σ²_n-2, получим, что

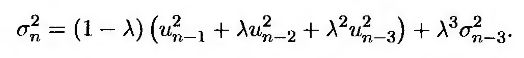
Продолжая в том же духе, в итоге придем к следующей формуле.

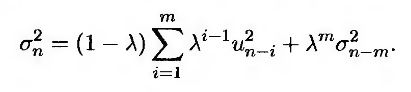
При больших значениях m член λ^mσ²_n-m становится очень малым и может быть отброшен, а формула (19.7) совпадет с формулой (19.4) при α_i = (1 – λ)λ^i-1. Таким образом, с течением времени показатель и убывает со скоростью λ, т.е. каждый последующий вес в λ раз больше предыдущего.

Пример 19.1

Предположим, что параметр λ равен 0,90, волатильность рыночного показателя в (n – 1)-й день равна 1% в день, а на протяжении (n – 1)-го дня рыночный показатель увеличился на 2%. Это значит, что σ²_n-1 = 0,01² = 0,0001 и u²_n-1 = 0,02² = 0,0004. Из формулы (19.7) следует, что

σ²_n = 0,9 x 0,0001 + 0,1 x 0,0004 = 0,00013.

Таким образом, оценка волатильности σ_п в течение n-го дня равна 0,00013, т.е. 1,14% в день. Обратите внимание на то, что ожидаемое значение величины u²_n-1 равно σ²_n-1, т.е. 0,0001. В нашем примере реальное значение величины u²_n-1 больше, чем ожидаемое, а оценка волатильности возрастает. Если бы реальное значение величины u²_n-1 было бы меньше ожидаемого, оценка волатильности уменьшилась бы.

Преимущество модели EWMA заключается в том, что для ее реализации не обязательно хранить большое количество данных. В любой момент времени достаточно помнить только текущую оценку дисперсии и самое последнее измеренное значение рыночного показателя. Измерив новое значение рыночного показателя, можно вычислить новое суточное относительное изменение и получить новую оценку дисперсии, применив формулу (19.7). Старую оценку дисперсии и старое значение рыночного показателя можно забыть.

Модель EWMA позволяет отслеживать изменения волатильности. Допустим, что в (п – 1)-й день рыночный показатель испытал скачок, т.е. величина u²_n-1 велика. В результате оценка текущей волатильности увеличится. Параметр λ определяет чувствительность оценки суточной волатильности к последним суточным изменениям. При малом значении λ основной вклад в оценку волатильности вносит величина u²_n-1. В таком случае оценка волатильности рыночного показателя на протяжении последовательных дней сама по себе характеризуется высокой волатильностью. При большом значении λ (близком к единице) оценки суточной волатильности мало чувствительны к новым суточным относительным изменениям рыночного показателя.

База данных RiskMetrics, созданная Дж. П. Морганом (L. Р. Morgan) в 1994 году для оценки суточной волатильности, использует модель EWMA с показателем λ = 0,94. Оказалось, что при таком выборе параметра λ предсказанные значения дисперсии широкого спектра рыночных показателей очень близки к реальным. В частности, реальное значение дисперсии в конкретный день было вычислено как среднее равновзвешенное значение величин u²_i, измеренных на протяжении последовательных 25 дней (см. задачу 19.17.)