19.5. Метод максимального правдоподобия

Рассмотрим способ вычисления параметров моделей с помощью ретроспективных данных, основанный на методе максимального правдоподобия (maximum likelihood method). Он предусматривает выбор значений параметров, при которых отношение правдоподобности становится максимальным.

Для начала проанализируем простой пример. Допустим, что в нашем распоряжении есть выборка цен 10 случайно выбранных акций в конкретный день и цена одной из них в течение этого дня упала, а цены остальных акций остались прежними или выросли. Как получить оптимальную оценку доли всех акций, цены которых упали? Естественно предположить, что эта доля равна 0,1. Теперь посмотрим, какие результаты дает применение метода максимального правдоподобия.

Допустим, что доля акций, цены которых упали, равна р. Вероятность того, что цена акции конкретной компании упадет, а цены акций остальных компаний останутся прежними или вырастут, равна р(1 – р). Метод максимального правдоподобия позволяет вычислить значение р, при котором выражение р(1 – р) достигает максимума. Дифференцируя это выражение по переменной р и приравнивая результат к нулю, получим, что максимум достигается при р = 0,1. Таким образом, мы получили ожидаемый результат.

Оценка постоянной дисперсии

В качестве другого примера рассмотрим задачу оценки дисперсии с помощью т значений переменной X, имеющей нормальное распределение с нулевым математическим ожиданием. Обозначим эти значения как u₁, u₂,..., и_т, а дисперсию – буквой v. Правдоподобие наблюдаемого значения u_i равно значению плотности вероятности случайной переменной X при X = u_i. Иначе говоря, оно равно

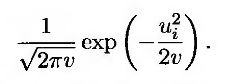
Правдоподобие т наблюдаемых значений, перечисленных в порядке их измерения, равно

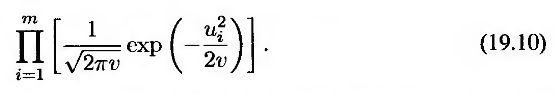
Используя метод максимального правдоподобия, приходим к выводу, что наилучшей оценкой переменной v является значение, при котором это выражение достигает максимума.

Максимизация этого выражения эквивалентна максимизации логарифма этого выражения. Логарифмируя выражение (19.10) и отбрасывая постоянные множители, сведем задачу к максимизации функции

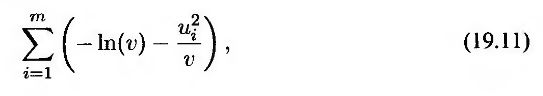
т.е.

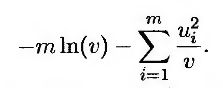
Дифференцируя это выражение по переменной v и приравнивая результат к нулю, получим, что оценка дисперсии по методу максимального правдоподобия равна

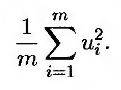
Оценка параметров модели GARCH(1,1)

Применим метод максимального правдоподобия для оценки параметров модели GARCH(1,1) или другой схемы оценки волатильности. Обозначим дисперсию в течение i-го дня как u_i = σ²i. Предположим, что величины u_i имеют нормальное распределение. Проводя вычисления, аналогичные описанным выше, сведем задачу вычисления оптимальных параметров к максимизации выражения

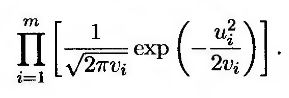
Логарифмируя, сведем задачу к максимизации выражения

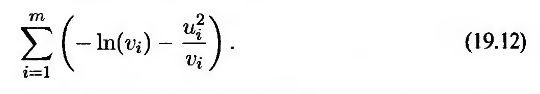
Оно совпадает с выражением (19.11), за исключением того, что в нем переменная v заменена значениями v_i. Оптимальные параметры, при которых выражение (19.12) достигает максимума, вычисляются с помощью итерационного метода.

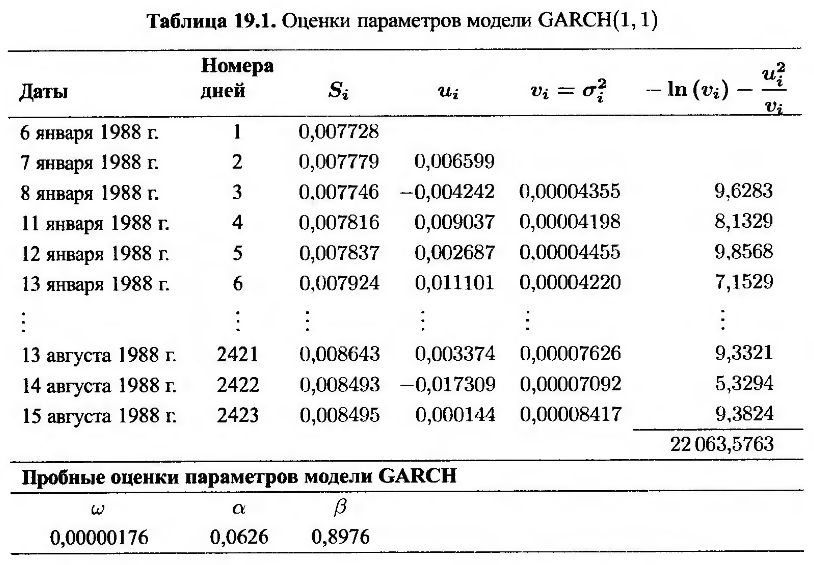
Данные, приведенные в табл. 19.1, показывают, как следует организовывать данные для модели GARCH(1,1). Таблица содержит данные анализа валютного курса японской иены за период с 6 января 1988 года по 15 августа 1997 года. Числа, записанные в табл. 19.1, представляют собой пробные оценки трех параметров модели GARCH(1,1) – ω, α и β. В первом столбце записаны даты, во втором – порядковые номера дней, в третьем – валютный курс S_i в конце i-го дня. В четвертом столбце содержатся пропорциональные изменения валютного курса за период, прошедший с конца (i – 1)-го дня до конца i-го дня, т.е. числа u_i = (S_i – S_i-1)/S_i-1)/S_i-1. В пятом столбце записаны оценки дисперсии v_i – σ²_i для i-го дня, вычисленные по данным, относящимся к концу (г – 1)-го дня. Дисперсия показателя на третий день устанавливается равной u²₂. В последующие дни для вычисления оценок дисперсии используется формула (19.9). Шестой столбец содержит меры правдоподобия – ln(v_i) – u²_i/v_i. Значения в пятом и шестом столбцах вычислены на основе текущих пробных оценок параметров ω, α и β. Эти параметры следует выбирать таким образом, чтобы сумма чисел, записанных в шестом столбце, достигала максимального значения. Для этого используется итерационная процедура.?

В нашем примере оптимальные значения параметров равны

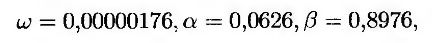
а максимальное значение выражения (19.12) равно 22063,5763. Числа, указанные в табл. 19.1, представляют собой результаты, полученные на последней итерации при вычислении оптимальных параметров ω, α и β.

Долговременная дисперсия V_L в нашем примере равна

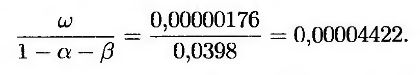
Долговременная волатильность равна √0,00004422, т.е. 0,665% в день.

График волатильности валютного курса японской иены за десятилетний период представлен на рис. 19.1. Как видим, большую часть времени волатильность колебалась в диапазоне от 0,4% до 0,8% в день, хотя иногда она выходила за пределы 1%.

Альтернативой модели GARCH(1,1) является метод дисперсионного таргетинга (variance targeting). В этом методе долговременная средняя дисперсия V_L приравнивается к выборочной дисперсии, вычисленной с помощью исходных данных, или другой разумно выбранной величине. Тогда параметр ω полагается равным V_L( 1 – α – β), и вычислять необходимо только оставшиеся два параметра. Из данных, приведенных в табл. 19.1, следует, что выборочная дисперсия равна 0,00004341, а суточная волатильность – 0,659%. Установив величину V_L равной выборочной дисперсии, приходим к выводу, что оптимальными значениями величин α и β являются числа 0,0607 и 0,8990 соответственно, а значение целевой функции равно 22 063,5274, т.е. чуть-чуть меньше, чем число 22 063,5763, вычисленное с помощью предыдущей процедуры.

Вычислительная процедура, основанная на модели EWMA, относительно проста. В ней параметры принимают следующие оптимальные значения: ω = 0, α = 1 – λ и β = λ, а оценке подлежит только один параметр. Как следует из табл. 19.1, значение параметра λ, при котором выражение (19.12) достигает максимального значения, равно 0,9686, а значение целевой функции равно 21 995,8377.

Для вычисления параметров, максимизирующих функцию правдоподобия, можно применить процедуру Solver программы Excel и реализовать модель GARCH(1,1) и метод EWMA. Эта процедура работает корректно, только если рабочий лист устроен так, что искомые параметры приблизительно совпадают. Например, в модели GARCH(1,1) ячейки A1, А2 и А3 могут содержать числа ω x 10⁵, α и 0,1β. Затем в ячейки B1, В2 и B3 необходимо записать числа А1/100000, А2 и 10*А3 соответственно. Для вычисления функции правдоподобия с помощью процедуры Solver следует использовать параметры, записанные в ячейках Bl, В2 и B3. Результаты вычислений будут записаны в ячейках A1, А2 и A3.

Насколько хороша модель?

В основе модели GARCH лежит предположение, что волатильность со временем изменяется. На протяжении одних периодов времени волатильность может быть высокой, а на протяжении других – низкой. Иначе говоря, если значения u²_i велики, то значения u²_i+1, u²_i+2, ... также, скорее всего, будут велики, а если значения u²_i малы, то значения u²_i+1, u²_i+2, ... также, скорее всего, будут малы. Проверить это утверждение можно с помощью исследования автокорреляционной структуры значений u².

Допустим, что значения u²_i демонстрируют наличие автокорреляции. Для того чтобы модель GARCH работала хорошо, следует исключить автокорреляцию. Для этого необходимо проанализировать автокорреляционную структуру переменных u²_i. Если эта проверка выявит незначительную автокорреляцию, то модель для оценки дисперсии σ_i будет правильно оценивать автокорреляцию переменных u²_i.

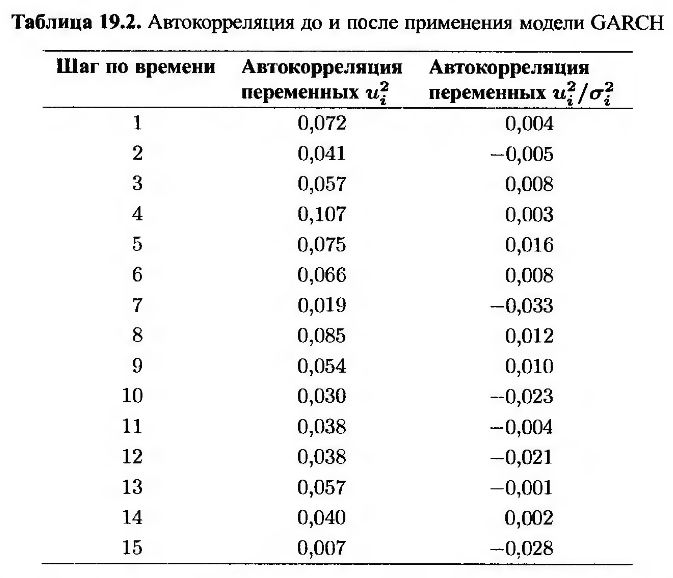
В табл. 19.2 приведены результаты анализа автокорреляции значений валютного курса японской иены до и после применения модели GARCH. В первом столбце приведены шаги по времени, на которых вычислялась автокорреляция. Во втором столбце записаны значения автокорреляции для переменных u²_i, а в третьем – для переменных u²_i/σ²_i. Анализ таблицы показывает, что для переменных u²_i автокорреляция при всех шагах по времени от 1 до 15 является положительной. Для переменных u²_i/σ²_i автокорреляция в некоторых случаях была положительной, а в некоторых – отрицательной. Однако по абсолютной величине автокорреляция переменных u²_i/σ²_i намного меньше, чем автокорреляция переменных u²_i.

Модель GARCH довольно точно объясняет поведение исходных данных. Для более глубокого анализа необходимо применить, например, хорошо известную статистику Льюнга-Бокса (Ljung-Box statistics). Для последовательности, состоящей из m наблюдений, статистика Льюнга-Бокса имеет следующий вид.

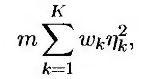
где параметр η_k представляет собой автокорреляцию с шагом K, и

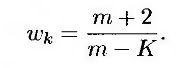
Если K = 15 и статистика Льюнга-Бокса больше, чем 25, то гипотезу о том, что автокорреляция равна нулю, можно отклонить с доверительным уровнем, равным 95%.

Из табл. 19.2 следует, что статистика Льюнга-Бокса для последовательности значений u²_i приблизительно равна 123. Это явно свидетельствует о наличии автокорреляции. Статистика Льюнга-Бокса для последовательности значений u²_i/σ²_i равна 8,2, т.е. после применения модели GARCH автокорреляция почти исчезла.