|
Рассмотрим модификации вычислительных процедур, описанных в главе 17, предназначенные для решения конкретных задач. Начнем с построения дерева для оценки деривативов, зависящих от предыстории.


Деривативы, зависящие от предыстории (path-dependent, or history dependent derivatives), – это производные финансовые инструменты, выигрыш которых зависит от всей траектории цены актива, а не только от ее последнего значения. Примерами деривативов, зависящих от предыстории, являются азиатские опционы и опционы “с оглядкой назад”. Как указано в главе 22, выигрыш азиатского опциона зависит от средней цены базового актива. В свою очередь, цена опциона “с оглядкой назад” зависит от минимальной или максимальной цены. Если аналитические формулы не позволяют оценить стоимость опционов, зависящих от предыстории, можно применить метод Монте-Карло, описанный в главе 17. Выборочную стоимость дериватива можно вычислить, предварительно сгенерировав случайную траекторию цены актива в риск-нейтральных условиях, вычислив выигрыш и сделав дисконт с учетом безрисковой процентной ставки. Чтобы получить оценку стоимости дериватива, необходимо вычислить большое количество выборочных значений стоимости, а затем усреднить их.
Основная проблема, связанная с применением метода Монте-Карло, заключается в том, что для достижения требуемой точности необходимо затратить неприемлемо большое количество вычислительного времени. Кроме того, с помощью этого метода трудно оценивать американские деривативы, зависящие от предыстории (т.е. деривативы, допускающие досрочное исполнение). В данной главе будет показано, как применить метод биномиального дерева, описанный в главе 17, для вычисления стоимости некоторых деривативов, зависящих от предыстории. Эта процедура позволяет оценить американские деривативы, зависящие от предыстории, причем ее эффективность при оценке аналогичных европейских опционов выше эффективности метода Монте-Карло.
Для применения этой процедуры необходимо выполнение двух условий.
1. Выигрыш дериватива должен зависеть от единственной функции F, описывающей траекторию базового актива.
2. Должна существовать возможность вычислять значения функции F в момент τ + Δt, по значениям функции F в момент τ и цене базового актива в момент τ + Δt.
Иллюстрация на основе опциона “с оглядкой назад”
В качестве иллюстрации рассмотрим американский опцион “с оглядкой назад” на покупку акций, не приносящих дивидендов. Если опцион исполняется в момент τ, то его выигрыш равен разнице между максимальной ценой актива на временном интервале от нуля до момента исполнения т и текущей ценой акции. Предположим, что текущая цена акции равна 50 долл., волатильность ее цены – 40% в год, безрисковая процентная ставка – 10% годовых, срок действия опциона – три месяца, а поведение цены акции описывается трехуровневым биномиальным деревом. Используя обычные обозначения, запишем эти данные в следующем виде: S0 = 50, σ = 0,4, r = 0,10, Δt = 0,08333, u = 1,1224, d = 0,8909, a = 1,0084 и p = 0,5073.
Дерево изображено на рис. 24.2. Верхнее число возле каждого узла означает цену акции. Ниже указаны максимальные цены акции, которые могли быть достигнуты на пути, ведущем к данному узлу. В самом низу приведены значения стоимости дериватива, соответствующие возможной максимальной цене.

Стоимость дериватива в конечных узлах дерева равна разности между максимальной и фактической ценами акции. Чтобы проиллюстрировать процедуру обратного обхода, предположим, что мы находимся в узле А, в котором цена акции равна 50 долл. Максимальная цена акции, достигнутая до сих пор, равна 56,12 долл. или 50 долл. Рассмотрим сначала ситуацию, в которой максимальная цена акции равна 50 долл. Если в дальнейшем она будет расти, то цена достигнет максимума, равного 56,12 долл., а стоимость дериватива окажется равной нулю. Если же цена станет падать, то максимум останется равным 50 долл., а стоимость дериватива будет равной 5,45 долл. Если не исполнять опцион досрочно, то его стоимость в узле А при условии, что достигнутый максимум равен 50 долл., составит
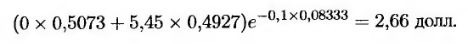
Очевидно, что досрочное исполнение опциона в узле А является нецелесообразным, поскольку выигрыш при этом равен нулю. Аналогичные вычисления в ситуации, когда достигнутый максимум равен 56,12 долл., при условии, что опцион не исполняется досрочно, приводят к следующему результату.
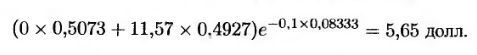
В данном случае досрочное исполнение принесет владельцу 6,12 долл. и представляется оптимальным решением. Обратный обход дерева показывает, что стоимость американского опциона “с оглядкой” равна 5,47 долл.
Обобщение
Если количество альтернативных значений функции F в каждом узле растет не так быстро, как количество временных шагов, то подход, описанный выше, оказывается неэффективным с вычислительной точки зрения. Рассмотренный выше пример не порождал таких проблем, поскольку количество альтернативных максимальных цен акции в узлах биномиального дерева, предусматривающего n шагов по времени, никогда не превышает числа n.
К счастью, этот подход допускает обобщение на ситуации, в которых в каждом узле существует большое количество альтернативных значений функции F. Основная идея заключается в следующем. В каждом узле выполняются вычисления лишь для небольшого количества репрезентативных значений функции F, а когда эти значения понадобятся для вычисления последующих величин, осуществляется интерполяция.
На первом этапе необходимо пройти все дерево и определить максимальное и минимальное значения функции F в каждом узле. Предположим, что значение функции F в момент времени τ + Δt зависит только от ее значения в момент τ и значения базовой переменной в момент τ + Δt. Тогда максимум и минимум этой функции можно вычислить непосредственно по ее значениям в узлах, соответствующим моменту τ. На втором этапе необходимо выбрать репрезентативные значения функции F в каждом узле. Здесь возможно большое количество вариантов. Например, можно просто выбрать в качестве репрезентативных значений максимум и минимум функции, а также числа, лежащие между ними на одинаковом расстоянии друг от друга. При обратном обходе дерева стоимость дериватива в каждом узле вычисляется для каждого репрезентативного значения функции F.
Продемонстрируем эти вычисления на примере 22.2, в котором требуется найти цену опциона “колл” по средней цене. Рассмотрим вариант, в котором выигрыш зависит от средней арифметической цены акции. Начальная цена акции равна 50 долл., цена исполнения – 50 долл., безрисковая процентная ставка – 10%, волатильность цены акции – 40%, а время, оставшееся до конца срока действия опциона, – один год. Используем дерево, содержащее 20 временных шагов. Его биномиальные параметры равны Δt, = 0,05, и = 1,0936, d = 0,9144, р = 0,5056 и 1 – р = 0,4944. Функция F представляет собой среднее арифметическое всех цен акций.
На рис. 24.3 показаны вычисления, выполненные для части этого дерева. Узел X является центральным узлом, соответствующим моменту времени, равному 0,2 года (конец четвертого временного интервала). Соседние узлы Y и Z соответствуют моменту времени, равному 0,25 года. Цена акции в узле X равна 50 долл. Прямая индукция показывает, что максимальная средняя цена акции, достигнутая ранее, равна 53,83 долл. Минимум равен 46,65. (При вычислении среднего значения учитывается как начальная, так и конечная цена акции.) Из узла X выходят две ветви: в узел Y и в узел Z. В узле Y цена акции равна 54,68 долл., а средняя цена колеблется от 47,99 до 57,39 долл. В узле Z цена акции равна 45,72 долл., а средняя цена колеблется от 43,88 до 52,48 долл.

Предположим, что в качестве репрезентативных средних цен были выбраны четыре равноотстоящих числа. Это значит, что для узла X репрезентативными считаются значения 46,65, 49,04, 51,44 и 53,83. В узле Y следует рассмотреть значения среднего, равные 47,99, 51,12, 54,26 и 57,39. Соответственно, в узле Z следует рассмотреть значения среднего, равные 43,88, 46,75, 49,61 и 52,48. Допустим, что для вычисления стоимости опциона, соответствующей каждому из альтернативных значений, используется обратная индукция. Эти значения показаны на рис. 24.3. Например, в узле Y стоимость опциона, соответствующая среднему курсу 51,12 долл., равна 8,101 долл.
Рассмотрим вычисления в узле X, когда средняя цена равна 51,44 долл. Если цена акции растет, мы попадем узел Y. В этом случае новое среднее значение будет равно
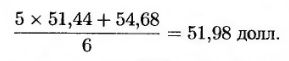
Стоимость опциона, соответствующую этой средней цене, можно определить с помощью интерполяции соседних значений средней цены: 51,12 и 54,26 долл. Эта стоимость равна
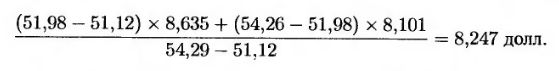
Аналогично, если цена акции падает, мы попадем в узел Z. В этом случае новое среднее значение будет равно
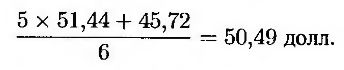
С помощью интерполяции приходим к выводу, что стоимость опциона, соответствующая этой средней цене, равна 4,182 долл.
Таким образом, стоимость дериватива в узле X, соответствующая средней цене, равной 51,44 долл., составляет
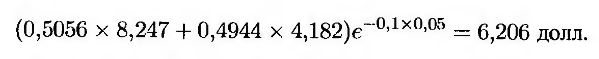
Другие значения стоимости у узле X вычисляются аналогично. Вычислив значения стоимости во всех узлах, соответствующих 0,2 года, можно перейти к узлам, соответствующим 0,15 года.
Стоимость опциона, вычисленная с помощью всего дерева, равна 7,17 долл. При увеличении количества шагов по времени и количества средних значений стоимость опциона сходится к правильному ответу. Если при вычислении используется 60 временнЫх шагов и 100 средних значений, стоимость опциона равна 5,58 долл. Аналитическая аппроксимация стоимости опциона, рассмотренного в примере 22.2, равна 5,62 долл.
Основное преимущество рассмотренного выше метода заключается в том, что он позволяет оценивать американские опционы. При этом вычисления совпадают с указанными, только к ним добавляется проверка целесообразности досрочного исполнения в каждом узле и при каждом альтернативном значении функции F. (На практике досрочное исполнение опциона часто зависит от обеих переменных: значения функции F и стоимости базового актива.) Рассмотрим американский вариант опциона «колл» по средней цене. Стоимости этого опциона, вычисленная с помощью биномиального дерева, содержащего 20 уровней и четыре альтернативных значения в каждом узле, равна 7,77 долл. Если количество шагов достигает 60, то стоимость равна 6,17 долл.
Описанный выше подход применяется в разнообразных ситуациях. Не следует, однако, забывать, что он корректен только, если выполняются два условия, указанные в начале раздела. Эффективность метода можно повысить, если вместо линейной интерполяции применять квадратичную.
|