|
С одной стороны, метод Монте-Карло очень удобен для оценки опционов, стоимость которых зависит от предыстории, а также опционов, в основе которых лежит много стохастических переменных. С другой стороны, при оценке американских опционов хорошо зарекомендовали себя деревья и конечно-разностные методы. А что делать, если стоимость американского опциона зависит от предыстории?


И как поступать в ситуациях, когда цены американских опционов зависят от нескольких стохастических переменных? В разделе 24.4 был описан способ модификации биномиальных деревьев для оценки некоторых опционов, зависящих от предыстории. Многие исследователи предложили использовать для вычисления стоимости американских опционов метод Монте-Карло. В этом разделе мы рассмотрим два альтернативных подхода.
Метод наименьших квадратов
Для того чтобы оценить американский опцион, в каждый момент времени необходимо сделать выбор между досрочным исполнением и ожиданием. Вычислить стоимость исполнения, как правило, довольно просто. Большое количество исследователей, включая Лонгстаффа (Longstaff) и Шварца (Schwarz), предложили способ определения стоимости ожидания на основе метода Монте-Карло. В рамках этого подхода в каждый момент времени, допускающий досрочное исполнения опциона, для определения наилучшего приближения его стоимости применяется метод наименьших квадратов. Проанализируем этот метод, используя вычислительный пример из работы Лонгстаффа-Шварца.
Рассмотрим трехлетний американский опцион на продажу бездивидендной акции, который можно исполнить в конце первого, второго или третьего года. Безрисковая процентная ставка равна 6% в год (при непрерывном начислении). Текущая цена акции равна 1,00 долл., а цена исполнения – 1,10 долл. Предположим, что мы смоделировали восемь траекторий цены акции, показанных в табл. 24.3. (Этот пример носит исключительно иллюстративный характер. На практике для оценки опциона необходимо сгенерировать намного больше траекторий.) Если опцион исполняется только в конце третьего года, его выигрыш равен его действительной стоимости. Этот факт указан в последнем столбце табл. 24.4.

Если в конце второго года опцион “пут” приносит выигрыш, владелец опциона должен решить, исполнять ли его досрочно. Из табл. 24.3 следует, что в конце второго года опцион приносит выигрыш, если цена акции проходит траекторию 1, 3, 4, 6 и 7. Для этих траекторий предлагается использовать приближенную зависимость
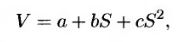
где S – цена акции, зарегистрированная в конце второго года, а V – стоимость продолжения опциона с учетом дисконта на конец второго года. Первые пять наблюдений цены S таковы: 1,08, 1,07, 0,97, 0,77 и 0,84. Из табл. 24.4 следует, что соответствующие значения переменной V равны 0,00, 0,07e_0’06xl, 0,18е-0’06х1, 0,20e-0,06x1 и 0.09е-0’06х1. Используя эти данные, для вычисления коэффициентов а, b и с необходимо минимизировать функцию
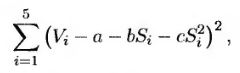
где Si и Vi – i-е наблюдения переменных S и V соответственно. Оказывается, a = –1,070, b = 2,983 и с = –1,813. Следовательно, зависимость, обеспечивающая наилучшую аппроксимацию данных, имеет следующий вид.
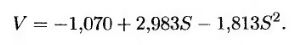
Итак, отказ от досрочного исполнения опциона в конце второго года, если цена акции прошла траектории 1, 3, 4, 6 и 7, приносит 0,0369, 0,0461, 0,1176, 0,1520 и 0,1565 долл. соответственно. Анализ табл. 24.3 показывает, что выигрыш от исполнения опциона в этот момент равен 0,02, 0,03, 0,13, 0,33 и 0,26 долл. соответственно. Это значит, что в конце второго года опцион целесообразно исполнить, если цена акции прошла траектории 4, 6 или 7. Денежные потоки по восьми путям, возникающие при досрочном исполнении опциона в конце второго или третьего года, приведены в табл. 24.5.
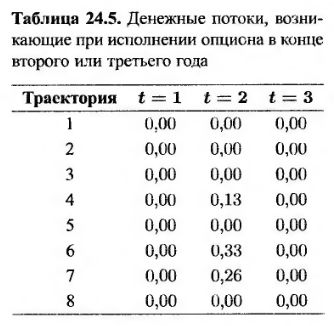
Рассмотрим теперь траектории цены акции, при которых опцион в конце первого года оказывается в выигрыше. К ним относятся траектории 1, 4, 6, 7 и 8. Из табл. 24.3 следует, что цены акции S в конце каждой из траекторий равны 1,09, 0,93, 0,76, 0,92 и 0,88 долл. соответственно. Значения переменной V для этих траекторий определяются по табл. 24.5. Они равны 0,00, 0,13e-0,06x1, 0,33е-0,06х1, 0,26е-0,06x1 и 0,00 соответственно. Зависимость, определенная по методу наименьших квадратов, имеет такой вид.
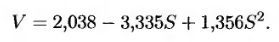
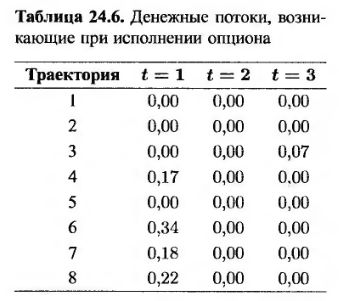
Таким образом, отказ от досрочного исполнения опциона в конце первого года, если цена акции прошла траектории 1, 4, 6, 7 или 8, приносит 0,0139, 0,1092, 0,2866, 0,1175 и 0,1533 долл. соответственно. Анализ табл. 24.3 показывает, что выигрыш от исполнения опциона в этот момент равен 0,01, 0,17, 0,34, 0,18 и 0,22 долл. соответственно. Это значит, что в конце первого года опцион целесообразно исполнить, если цена акции прошла траектории 4, 6, 7 или 8. Денежные потоки, возникающие при досрочном исполнении опциона в конце первого, второго или третьего годов, приведены в табл. 24.6. Стоимость опциона в начальный момент времени определяется с помощью применения дисконта с безрисковой процентной ставкой к каждому из полученных результатов с последующим усреднением. Это приводит нас к следующему ответу.
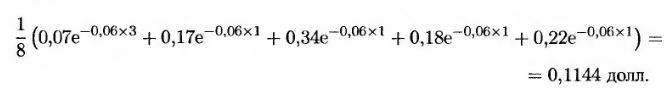
Поскольку эта величина больше 0,10, немедленно исполнять опцион нецелесообразно.
Этот метод имеет много модификаций. Если опцион допускает досрочное исполнение в любой момент времени, то его стоимость можно аппроксимировать, рассмотрев большое количество точек исполнения (как это делается при построении биномиального дерева). Кроме того, зависимость между величинами V и S может быть более сложной. Например, она может быть не квадратичной, а кубической. Если досрочное исполнение опциона зависит от нескольких переменных состояния, следует поступать так, как описано выше. Затем следует сформулировать функциональную зависимость между переменными V и переменными состояния и определить ее неизвестные параметры с помощью метода наименьших квадратов.
Параметризация границы исполнения
Множество исследователей, в частности Андерсен (Andersen), предложили альтернативный подход, основанный на параметризации границы исполнения (exercise boundary) и итерационном определении оптимальных параметров, передвигаясь от конца действия опциона к его началу. Для иллюстрации вернемся к примеру, связанному с опционом на продажу акций, не приносящих дивидендов, и предположим теперь, что в ходе моделирования были снова сгенерированы восемь траекторий цены акции, представленные в табл. 24.3. В этом случае досрочное исполнение опциона в момент t можно параметризовать критической ценой акции S*(t). Если цена акции в момент t меньше величины S*(t), опцион исполняется досрочно, если же цена акции больше значения S*(t), опцион не исполняется. Значение S*(3) равно 1,10 долл. Если цена акции в этот момент (т.е. в конце срока действия опциона) больше 1,10 долл., то опцион не исполняется. Если же цена акции в конце третьего года меньше 1,10 долл., то опцион исполняется. Рассмотрим способ определения значения S*(2).
Предположим, что мы выбрали значение S*(2) меньшим 0,77. В этом случае опцион в конце второго года не исполняется ни в одном из восьми вариантов. Стоимость опциона в конце второго года для каждой из восьми траекторий равна 0,00, 0,00, 0,07e-0,06x1, 0,18e-0,06x1, 0,00, 0,20e-0,06x1, 0,09e-0,06x1 и 0,00 соответственно. Среднее значение этих величин равно 0,0636. Допустим теперь, что S*(2) = 0,77. Тогда стоимость опциона в конце второго года для каждой из восьми траекторий равна 0,00, 0,00, 0,07e-0,06x1, 0,18e-0,06x1, 0,00, 0,33, 0,09e-0,06x1 и 0,00 соответственно. Среднее значение этих величин равно 0,0813. Аналогично, если значение S*(2) равно 0,84, 0,97, 1,07 и 1,08, стоимость опциона в конце второго года для каждой из соответствующих траекторий равна 0,1032, 0,0982,0,0938 и 0,0963 соответственно. Этот анализ показывает, что оптимальное значение S*(2) (т.е. такое, при котором достигается максимальная средняя стоимость) равно 0,84. (Точнее, значение S*(2) следует выбирать в диапазоне 0,84 ≤ S*(2) < 0,97.) Если выбрать оптимальное значение S*(2), то стоимость опциона в конце второго года для каждой из восьми траекторий станет равной 0,00, 0,00, 0,0659, 0,1695, 0,00, 0,33, 0,26 и 0,00 соответственно. Средняя стоимость опциона равна 0,1032 долл.
Перейдем к вычислению величины S*(l). Если S*(l) < 0,76, то опцион в конце второго года не исполняется ни в одном из восьми вариантов, а его стоимость в конце второго года равна 0,1032е-0’06x1 = 0,0972. Если S*(l) = 0,76, то стоимость опциона в конце второго года для каждой из восьми траекторий равна 0,00, 0,00, 0,0659e-0,06x1, 0,1695е-0,06x1, 0,00, 0,34, 0,26е-0,06x1 и 0,00 соответственно. Среднее значение этих величин равно 0,1008. Аналогично, если значение 5*(1) равно 0,88, 0,92, 0,93 и 1,09, то средняя стоимость опциона в конце второго года для каждой из соответствующих траекторий равна 0,1283, 0,1202, 0,1215 и 0,1228 соответственно. Таким образом, анализ показывает, что оптимальное значение S*(l) равно 0,88. (Точнее, значение S*(l) следует выбирать в диапазоне 0,88 ≤ S*(l) < 0,92.) Стоимость опциона в нулевой момент времени при условии отказа от его досрочного исполнения равна 0,1283е-0,06x1 = 0,1208. Эта величина больше, чем 0,10 долл., которые можно получить, досрочно исполнив опцион в начальный момент времени.
На практике для определения границы исполнения опциона необходимо провести десятки тысяч сеансов моделирования. Получив границу досрочного исполнения, траектории цены акции следует отбросить и выполнить новый сеанс моделирования по методу Монте-Карло, используя вычисленную границу. Рассмотренный американский опцион на продажу акций является достаточно простым, поскольку границы исполнения опциона в любой момент времени можно определить по ценам акции. В более сложных ситуациях необходимо выполнить параметризацию границы досрочного исполнения.
Верхние границы
Оба описанных подхода недооценивают стоимость американских опционов, поскольку они используют субоптимальные границы досрочного исполнения. Это побудило Андерсена и Броуди (Broadie) предложить процедуру для уточнения верхней границы стоимости опциона. В сочетании с любым методом вычисления нижней границы стоимости опциона эта процедура позволяет уточнить истинную стоимость американского опциона.
|