25.1. Рыночная цена риска

Для начала рассмотрим свойства деривативов, зависящих от одной переменной θ. Предположим, что процесс, описывающий переменную θ, имеет следующий вид.

где dz – винеровский процесс. Параметры т и s представляют собой ожидаемую скорость роста переменной в и ее волатильность соответственно. Предположим, что эти параметры зависят только от переменной в и времени t. Переменная в не обязана быть ценой некоего инвестиционного актива. Она может вообще не иметь отношения к финансовому рынку и представлять собой, например, температуру в центре Нового Орлеана.

Допустим, что f₁ и f₂ – цены двух производных финансовых инструментов, зависящих только от переменных θ и t. Эти деривативы могут быть опционами или другими ценными бумагами, приносящими выигрыш, равный значению некоторой функции, зависящей от переменной θ в будущий момент времени. Будем считать, что на протяжении всего периода, на котором регистрируются значения функций f₁ и f₁, деривативы не приносят дохода.

Предположим, что функции f₁ и f₂ подчиняются следующим стохастическим процессам:

и

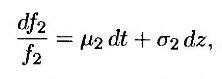
где μ₁, μ₂, σ₁ и σ₂ – функции, зависящие от переменных θ и t. Символы dz обозначают винеровский процесс, указанный в уравнении (25.1), поскольку он является единственным источником неопределенности цен Д и Д. Дискретные аналоги этих процессов выглядят следующим образом.

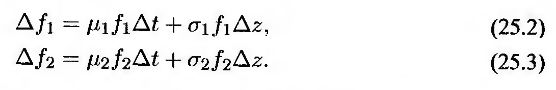
Величину Δz можно исключить, сформировав мгновенно безрисковый инвестиционный портфель, состоящий из σ₂f₂ единиц первого дериватива и – σ₁f₁ единиц второго дериватива. Обозначим стоимость этого портфеля буквой П. Тогда справедливо следующее соотношение:

Отсюда следует, что

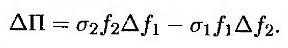
Подставляя в уравнение (25.4) выражения (25.2) и (25.3), получим

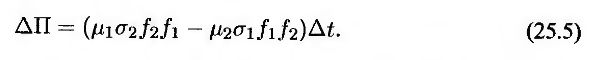
Поскольку инвестиционный портфель является мгновенно безрисковым, его доходность должна быть равной безрисковой процентной ставке. Следовательно,

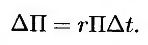
Подставляя в это уравнение выражения (25.4) и (25.5), приходим к выводу, что

т.е.

Обратите внимание на то что левая часть равенства (25.6) зависит только от параметров процесса, описывающего изменение цены f₁, а правая часть этого равенства зависит только от параметров процесса, описывающего изменение цены f₂. Обозначим левую и правую части равенства (25.6) буквой λ.

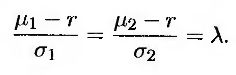
Отбросив индексы, можно показать, что если функция f представляет собой цену дериватива, зависящего только от переменных θ и t, и является решением уравнения

то

Параметр λ называется рыночной ценой риска, связанного с переменной θ (market price of risk of θ). Он может зависеть от обеих переменных θ и t, но не от природы дериватива f. В любой момент времени величина (μ – r)/σ должна быть одинаковой для всех деривативов, зависящих только от переменных θ и t.

Следует отметить, что величина σ, которую мы назвали волатильностью цены f, представляет собой коэффициент, стоящий перед dz в уравнении (25.7). Она может быть как положительной, так и отрицательной. Если волатильность s переменной θ является положительной, а функция f является возрастающей по переменной θ (т.е. производная δf/δθ является положительной), то величина σ является положительной. Если же функция f является убывающей по переменной θ, то величина σ является отрицательной. Традиционная волатильность функции f равна |σ|.

Рыночная цена риска, связанного с переменной θ, измеряет баланс между риском и доходностью ценных бумаг, зависящих от переменной θ. Равенство (25.8) можно переписать следующим образом.

Чтобы дать интуитивно понятное описание этого равенства, отметим, что переменную σ можно приближенно интерпретировать как величину риска, связанного с функцией f, обусловленную влиянием переменной θ. Следовательно, в правой части равенства стоит величина риска, связанного с переменной θ, умноженная на его цену. Левая часть равенства представляет собой разность между ожидаемой доходностью и безрисковой процентной ставкой, которая должна компенсировать существующий риск. Равенство (25.9) является аналогом модели оценки капитальных активов, связывающей избыточную доходность акций с их риском.

В главе не рассматриваются вопросы, связанные с измерением рыночной цены риска. Они будут изучены в главе 31 при оценке реальных опционов.

В главе 5 были описаны различия между инвестиционными и потребительскими активами. Инвестиционными активами называются товары и ценные бумаги, которые покупаются и продаются исключительно с инвестиционными целями большим количеством инвесторов. Они используются в качестве элементов торговых стратегий при формировании безрисковых инвестиционных портфелей. Потребительские активы предназначены для потребления и не используются для инвестиций. Если θ – цена инвестиционного актива, то должно выполняться соотношение

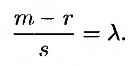
Однако если θ – цена потребительского актива, это соотношение не всегда является истинным.

Пример 25.1

Рассмотрим дериватив, цена которого положительно связана с ценой нефти и не зависит от других стохастических переменных. Допустим, что ожидаемая доходность этого дериватива равна 12% годовых, а волатильность – 20% в год. Предположим также, что безрисковая процентная ставка равна 8% годовых. Следовательно, рыночная цена риска, связанного с ценой нефти, равна

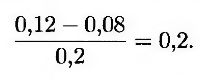
Отметим, что нефть является потребительским, а не инвестиционным активом. Следовательно, ее рыночную цену риска нельзя вычислить с помощью равенства (25.8), положив величину μ равной ожидаемой доходности нефтяных инвестиций, а величину σ – равной волатильности цены на нефть.

Пример 25.2

Рассмотрим две ценные бумаги, положительно связанные с 90-дневной процентной ставкой. Допустим, что ожидаемая доходность первой ценной бумаги равна 3% годовых, а ее волатильность – 20% в год. Предположим также, что волатильность второй ценной бумаги равна 30% годовых, а мгновенная безрисковая процентная ставка равна 6% годовых. Следовательно, рыночная цена риска, связанного с процентной ставкой, для первой ценной бумаги равна

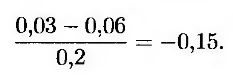
Используя равенство (25.9), ожидаемую доходность второй ценной бумаги можно вычислить следующим образом.

т.е. 1,5% годовых.

Альтернативные условия

Цена дериватива f подчиняется следующему стохастическому процессу.

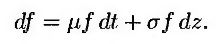
Величина μ зависит от рисковых предпочтений инвесторов. Если рыночная цена риска равна нулю, то величина λ равна нулю. Из равенства (25.9) следует, что μ = r, поэтому процесс, описывающий изменение функции f, имеет следующий вид.

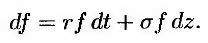
Эти ограничения мы будем называть традиционными риск-нейтральными условиями (traditional risk-neutral world).

Другие предположения о рыночной цене риска порождают альтернативные внутренне непротиворечивые условия. В целом, если рыночная цена риска равна λ, из равенства (25.9) следует, что

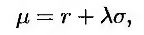
так что

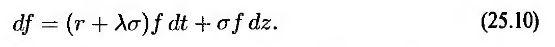
Рыночная цена риска, связанного с определенной переменной, определяет скорость роста стоимости всех ценных бумаг, зависящих от этой переменной. При изменении рыночной цены риска ожидаемая скорость роста ценных бумаг изменяется, но их волатильность остается прежней. Это явление было проиллюстрировано в разделе 11.7.

Выбор конкретной рыночной цены риска иногда называют определением вероятностной меры (probability measure). При некотором значении рыночной цены риска мы получим “реальные условия” и скорости роста стоимости ценных бумаг, наблюдаемые на практике.