25.4. Альтернативные варианты масштаба цен

Рассмотрим примеры, иллюстрирующие применение теоремы об эквивалентной мартингальной мере. В первом примере показано, что этот результат не противоречит традиционной риск-нейтральной теории расчетов, использованной ранее. В других примерах закладываются основы для вычисления стоимости опционов на облигации, процентных опционов “кэп” и свопционов, которые будут рассмотрены в главе 26.

Использование в качестве масштаба цен депозитного счета денежного рынка

Долларовый депозитный счет денежного рынка можно интерпретировать как ценную бумагу, стоимость которой в нулевой момент времени равна одному доллару, а доходность в любой момент времени равна мгновенной безрисковой процентной ставке r. Переменная r может быть стохастической. Если переменную g считать эквивалентом депозитного счета денежного рынка, то сумма на нем будет возрастать со скоростью r, т.е.

Дрейф переменной g носит стохастический характер, но ее волатильность равна нулю. Следовательно, форвардные риск-нейтральные условия относительно переменной g означают, что рыночная цена риска равна нулю. Эти риск-нейтральные условия называются традиционными. Из равенства (25.15) следует, что

где Е – математическое ожидание в традиционных риск-нейтральных условиях.

В данном случае g₀ = 1 и

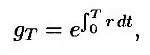
так что

т.е.

Из этого равенства следует, что оценить процентный дериватив можно, моделируя краткосрочную процентную ставку r в традиционных риск-нейтральных условиях. При каждом испытании следует вычислить ожидаемый выигрыш, а затем дисконтировать его по средней краткосрочной ставке, вычисленной по выборочной траектории.

Если краткосрочная процентная ставка r считается постоянной, уравнение (25.19) сводится к следующему виду.

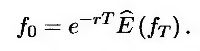
Эта формула представляет собой риск-нейтральное соотношение, которое мы уже использовали в предыдущих главах.

Использование в качестве масштаба цен стоимости облигации с нулевым купоном

Пусть P(t,T) – цена облигации с нулевым купоном в момент t при условии, что в момент Т выплата равна одному доллару. Рассмотрим последствия, которые возникают, если положить функцию g равной Р (t, Т). Через Е_T будем обозначать математическое ожидание в форвардных риск-нейтральных условиях относительно функции P(t,T). Поскольку g_T = Р (Т, Т) = 1 и g₀ = Р(0, Т), из равенства (25.15) следует, что

Обратите внимание на разницу между равенствами (25.20) и (25.19). В равенстве (25.19) дисконтирование выполняется внутри оператора математического ожидания. В то же время в равенстве (25.20) дисконтирование, представленное множителем Р(0, Т), выполняется вне этого оператора. Форвардные риск-нейтральные условия относительно функции P(t, Т) значительно упрощают расчеты для ценных бумаг, выплаты по которым осуществляются только в момент Т.

Рассмотрим переменную θ, которая не является процентной ставкой. Форвардный контракт на переменную θ, истекающий в момент Т, представляет собой контракт, по которому в момент Т осуществляются выплаты в размере θ_T – K, где θ_T – величина переменной θ в момент Т. Пусть f – стоимость этого форвардного контракта. Из формулы (25.20) следует, что

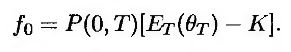
Форвардная цена F переменной θ равна величине К, при которой цена f₀ равна нулю. Следовательно,

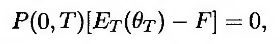
т.е.

Из формулы (25.21) следует, что форвардная цена любой переменной (за исключением процентной ставки) равна ее будущей цене спот в форвардных риск-нейтральных условиях относительно P(t, T). Рассуждения, изложенные в разделе 14.7, свидетельствуют о том, что фьючерсная цена переменной представляет собой ожидаемую в будущем цену спот в традиционном риск-нейтральном мире. Из равенства (25.20) следует, что оценить стоимость любых ценных бумаг, выплаты по которым осуществляются в момент Т, можно, вычислив ожидаемый размер выплаты при форвардных риск-нейтральных условиях относительно цены облигации, подлежащей погашению в момент Т, с последующим дисконтированием по безрисковой процентной ставке, установленной на это время. Формула (25.21) подтверждает предположение о том, что при вычислении ожидаемого размера выплат ожидаемая стоимость базового актива равна его форвардной стоимости.

Эти результаты являются принципиально важными для понимания стандартной модели рынка опционов на облигации, описанной в следующей главе.

Процентные ставки в моделях, использующих в качестве масштаба цен стоимость облигации

Пусть R(t, Т, Т*) – форвардная процентная ставка, установленная в момент t на временной промежуток между моментами Т и Т* при условии, что период начисления равен Т* – Т. (Это значит, что если Т* – Т = 0,5, то процентная ставка начисляется раз в полгода; если Т* – Т = 0,25, то раз в квартал и т.д.) В момент t форвардная цена облигации с нулевым купоном, действующей в промежутке между моментами Т и Т*, равна

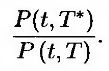
Форвардная процентная ставка определяется не так, как форвардная величина большинства переменных. Поскольку форвардная процентная ставка представляет собой процентную ставку, обусловленную соответствующей форвардной ценой облигации, выполняется следующее равенство.

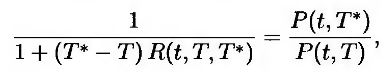
т.е.

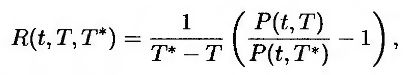
или

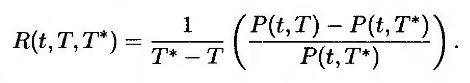
Если положить

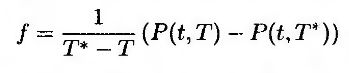
и g = P(t, T*), то по теореме об эквивалентной мартингальной мере функция R(t, Т, T*) представляет собой мартингал в форвардных риск-нейтральных условиях относительно функции R(t, Т*). Это значит, что

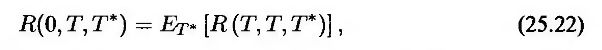
где E_T – математическое ожидание в форвардных риск-нейтральных условиях относительно функции R(t, T*).

Итак, мы показали, что форвардная процентная ставка эквивалентна ожидаемой будущей процентной ставке в форвардных риск-нейтральных условиях относительно цены облигации с нулевым купоном, выплаты по которой осуществляются в момент Т*. Этот результат в сочетании с равенством (25.20) имеет чрезвычайно большое значение для анализа стандартной модели рынка при оценке процентных опционов “кэп” в следующей главе.

Использование в качестве масштаба цен рентной ставки

В качестве следующего примера применения теоремы об эквивалентной мартингальной мере рассмотрим своп, вступающий в действие в будущий момент Т с моментами выплат Т_i, Т₂, ..., Т_N. Положим T₀ = Т. Предположим, что основная сумма свопа равна одному доллару. Допустим также, что форвардная ставка свопа (т.е. фиксированная процентная ставка, обесценивающая своп) в момент t(t ≤ Т) равна s(t). Стоимость фиксированной позиции в свопе равна

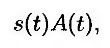
где

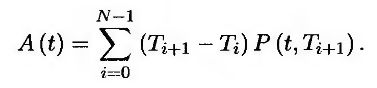
В главе 7 показано, что если в момент последней выплаты к ней добавляется основная сумма, стоимость плавающей позиции в свопе в момент вступления свопа в действие равна основной сумме. Отсюда следует, что если в момент к основной сумме добавить один доллар, то стоимость плавающей позиции в свопе в момент T₀ будет равна одному доллару. Стоимость одного доллара, полученного в момент T_N, в момент t будет равна P(t, Т_N). Следовательно, стоимость одного доллара, полученного в момент T₀, в момент t₀ будет равна P(t, T₀). Таким образом, стоимость плавающей позиции в момент t равна

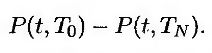
Приравнивая стоимости фиксированной и плавающей позиций, получим равенство

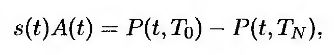
т.е.

Чтобы применить теорему об эквивалентной мартингальной мере, определим функцию f как разность P(t, T₀) – P(t, T_N), а функцию g будем считать равной A(t). Это приводит нас к следующей формуле.

Здесь E_A – математическое ожидание при форвардных риск-нейтральных условиях относительно функции A(t). Следовательно, при этих условиях ожидаемая будущая ставка свопа равна текущей ставке свопа.

Для любой ценной бумаги f из равенства (25.15) следует, что

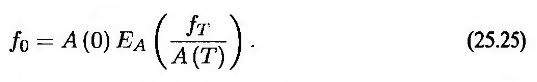
Этот результат в сочетании с уравнением (25.24) имеет большое значение для понимания стандартной модели рынка европейских свопционов, рассмотренной в следующей главе.