27.1. Поправки на выпуклость

Рассмотрим финансовый инструмент, предусматривающий в момент Т выплату, размер которой зависит от доходности облигации, наблюдаемой в этот момент.

Как правило, форвардная величина переменной S вычисляется по форвардному контракту, размер выплаты по которому в момент Т равен S_T – К. Именно величина К гарантирует, что стоимость контракта равна нулю. Как указано в разделе 25.4, форвардные процентные ставки и форвардная доходность определяются по-разному. Форвардная процентная ставка – это ставка, обусловленная форвардной стоимостью нуль-купонной облигации. Иначе говоря, форвардная доходность облигации представляет собой доходность, обусловленную форвардной стоимостью облигации.

Пусть В_T – цена облигации в момент Т, у_T – ее доходность и величины В_T и у_T связаны между собой отношением

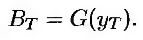
Обозначим через F₀ форвардную цену облигации в нулевой момент времени в рамках контракта, срок действия которого истекает в момент Т, а через у₀ – форвардную доходность облигации в нулевой момент времени. Из определения форвардной доходности облигации следует, что

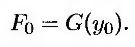
Функция G является нелинейной. Это значит, что в ситуации, когда ожидаемая будущая цена облигации равна ее форвардной цене (т.е. в форвардных риск-нейтральных условиях относительно облигации с нулевым купоном, срок обращения которой завершается в момент Т), ожидаемая будущая доходность облигации не равна ее форвардной доходности.

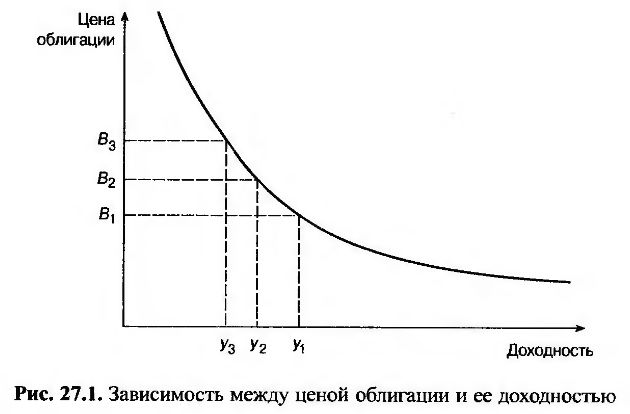
Это утверждение проиллюстрировано на рис. 27.1, демонстрирующем зависимость между ценой облигации и ее доходностью в момент Г. Для простоты предположим, что цена может принимать только три значения – В₁, B₂ и В₃ – причем все эти значения в форвардных риск-нейтральных условиях относительно P(t, Т) являются равновероятными. Предположим, что значения цены облигации являются равноотстоящими, т.е. В₂ – В₁ = В₃ – В₂. Ожидаемая цена облигации равна В₂ и совпадает с ее форвардной ценой. Значения цены облигации соответствуют трем значениям ее доходности – у₁, у₂ и у₃, которые не являются равноотстоящими. Переменная у₂ представляет собой форвардную доходность облигации, поскольку она соответствует форвардной цене облигации. Ожидаемая доходность облигации равна среднему арифметическому значению чисел у₁, y₂ и у₃. Очевидно, что эта доходность больше, чем у₂.

Рассмотрим теперь дериватив, размер выплаты по которому зависит от доходности облигации в момент Т. Из равенства (25.20) следует, что стоимость этого дериватива можно определить, 1) вычислив ожидаемый выигрыш в форвардных риск-нейтральных условиях относительно облигации с нулевым купоном, срок обращения которой завершается в момент Т, и 2) сделав дисконт по текущей безрисковой процентной ставке, установленной на момент Т.

Как известно, при таких условиях ожидаемая цена облигации равна ее форвардной цене. Следовательно, нам необходимо определить значение ожидаемой доходности облигации, при котором ожидаемая цена облигации равна ее форвардной цене. Анализ, проведенный в приложении 27.1, показывает, что приближенное выражение для искомой ожидаемой доходности облигации имеет следующий вид.

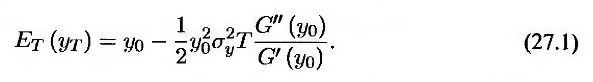
Здесь G' и G" – первая и вторая производные функции G, Е_T – математическое ожидание в форвардных риск-нейтральных условиях относительно P(t, Т), а σ_y – волатильность форвардной доходности. Следовательно, ожидаемый выигрыш можно дисконтировать по текущей безрисковой процентной ставке, установленной на момент Т при условии, что ожидаемая доходность облигации равна

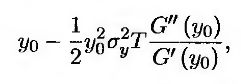
а не y₀. Разность между ожидаемой доходностью облигации и ее форвардной доходностью равна

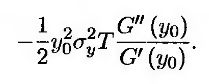
Эта величина называется поправкой на выпуклость (convexity adjustment). Она соответствует разности между величиной y₂ и ожидаемой доходностью, изображенной на рис. 27.1. (Поправка на выпуклость является положительной, поскольку G'(y₀) < 0 и G''(y₀ > 0.)

Приложение 1: процентные ставки

В качестве первого приложения формулы (27.1) рассмотрим финансовый инструмент, создающий в момент Т денежный поток, величина которого определяется путем применения к основной сумме L процентной ставки, установленной на промежуток времени между моментами Т иТ*. (Этот пример окажется полезным при анализе свопов по ставке LIBOR (LIBOR-in-Arrears) в главе 30.) Следует подчеркнуть, что процентная ставка, установленная на промежуток времени между моментами Т и Т*, как правило, выплачивается в момент Т*, однако здесь мы будем считать, что она выплачивается раньше – в момент Т.

Денежный поток в момент Т, создаваемый анализируемым нами финансовым инструментом, равен LR_Tτ, где τ = Т* – Т, & R_T – нуль-купонная процентная ставка, установленная на промежуток времени между моментами Т и Т* и выраженная с учетом периода начисления τ. Переменную R_T можно интерпретировать как доходность облигации с нулевым купоном, срок обращения которой истекает в момент Т*. Зависимость между ценой этой облигации и ее доходностью имеет следующий вид.

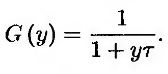
Из формулы (27.1) следует, что

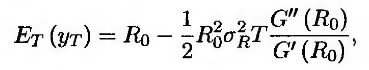
или

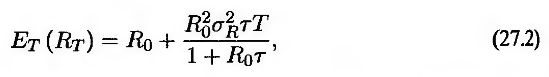
где R₀ – форвардная ставка, установленная на период времени между моментами Т и Т*, а σ_R – волатильность форвардной ставки.

Следовательно, стоимость изучаемого финансового инструмента равна

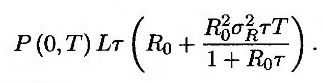
Пример 27.1

Рассмотрим дериватив, предусматривающий через три года выплату, размер которой равен сумме, полученной после умножения 1000 долл. на однолетнюю нуль-купонную ставку (начисляемую ежегодно), установленную на этот момент. Предположим, что нулевая ставка по всем срокам погашения равна 10% годовых с ежегодным начислением, а волатильность форвардной ставки, установленной на период времени между третьим и четвертым годами, равна 20%. В таком случае R₀ = 0,10, σ = 0,20, Т = 3 и Р(0,3) = 1/1.10³ = 0,7513. Стоимость дериватива равна

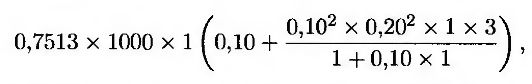
т.е. 75,95 долл. (Эта величина сравнима с ценой, равной 75,13 долл., вычисленной без поправки на выпуклость.)

Приложение 2: ставки свопа

Рассмотрим дериватив, предусматривающий в момент Т выплату, размер которой равен ставке свопа, установленной на этот момент. Ставка свопа равна номинальной доходности. Для вычисления поправки на выпуклость воспользуемся аппроксимацией и предположим, что JV-летняя ставка свопа в момент Т равна соответствующей доходности N-летней облигации с купоном, который равен сегодняшней форвардной ставке свопа. Это позволит нам использовать формулу (27.1).

Пример 27.2

Рассмотрим финансовый инструмент, предусматривающий через три года выплату, размер которой равен трехлетней ставке свопа, умноженной на 100 долл. Предположим, что выплаты по свопу осуществляются раз в год, нулевая ставка по всем срокам погашения равна 12% годовых при непрерывном начислении, волатильность трехлетней форвардной ставки (обусловленной ценами свопционов) через три года будет равна 22%. Ставка свопа аппроксимируется доходностью 12%-ной облигации, поэтому в качестве релевантной функции G(y) следует выбрать следующую зависимость.

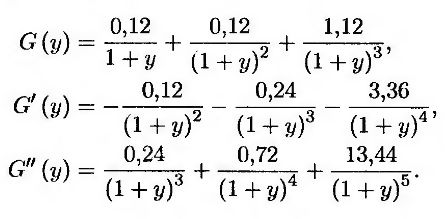
В таком случае форвардная доходность y₀ равна 0,12, так что G'(y₀) = –2,4018 и G"''(y₀) = 8,2546. По формуле (27.1) получаем, что

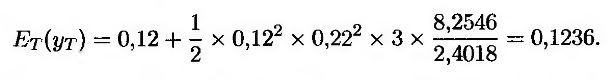
Таким образом, при оценке финансового инструмента форвардную ставку свопа следует считать равной 0,1236 (= 12,36%), а не 0,12. Стоимость анализируемой ценной бумаги равна

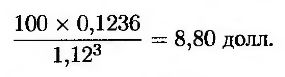
(Эта величина сравнима с ценой, равной 8,54 долл., вычисленной без поправки на выпуклость.)