Использование традиционных риск-нейтральных мер

Форвардная риск-нейтральная мера, использованная нами ранее, хорошо работает только, если выплата осуществляется один раз. В других ситуациях иногда более удобными оказываются традиционные риск-нейтральные меры. Предположим, что нам известен стохастический процесс, описывающий поведение переменной V в традиционных условиях, риск-нейтральных относительно валюты Y, и требуется оценить процесс, описывающий поведение этой переменной в традиционных условиях, риск-нейтральных относительно валюты X.

Введем следующие обозначения.

S: валютный спот-курс (количество единиц валюты Y за одну единицу валюты X);

σ_S: волатильность переменной S;

σ_V: волатильность переменной V;

ρ: мгновенная корреляция между переменными S и V.

В данном случае изменение масштаба цен происходит при замене счета денежного рынка в валюте Y счетом денежного рынка в валюте X (при этом оба счета денежного рынка номинируются в валюте X). Пусть gх – стоимость депозитного счета денежного рынка, номинированная в валюте X, а gу – стоимость депозитного счета денежного рынка, номинированная в валюте Y. Масштабный коэффициент равен

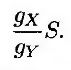
Как показано в разделе 25.4, переменные gх и gу имеют стохастический дрейф и нулевую волатильность. Кроме того, по лемме Ито волатильность масштабного коэффициента равна σ₁. Таким образом, изменение масштаба приводит к увеличению ожидаемой скорости роста переменной V на величину

При этом рыночная цена риска изменяется от нуля до ρσ_S.

Одним из применений этого результата является парадокс Сигела (Siegel’s paradox), описанный во врезке “Пример из деловой практики 27.1”.

Пример 27.5

Предположим, что двухлетний американский опцион приносит выигрыш в размере S – К фунтов стерлингов, где S – значение фондового индекса S&P 500 в момент исполнения опциона, а К – цена исполнения. Текущий уровень индекса S&P 500 равен 1 200 пунктам. Безрисковые процентные ставки в фунтах стерлингов и долларах равны 5 и 3% соответственно, коэффициент корреляции между обменным курсом доллар-фунт стерлингов и индексом S&P 500 равен 0,2, волатильность индекса S&P 500 равна 25%, а волатильность обменного курса – 12%. Доходность индекса S&P 500 равна 1,5%.

Чтобы оценить этот опцион, построим биномиальное дерево, описывающее поведение индекса S&P 500, используя в качестве масштаба счет денежного рынка в Великобритании (т.е. используя традиционные риск-нейтральные условия с точки зрения инвестора из Великобритании). Как показано выше, изменение масштаба цен приводит к увеличению ожидаемой скорости роста на величину

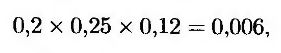
т.е. на 0,6%. Скорость роста индекса S&P 500 в долларовом масштабе равна 3 – 1,5 = 1,5%. Следовательно, скорость роста индекса S&P 500 в масштабе фунта стерлингов равна 2,1%. Безрисковая процентная ставка в фунтах стерлингов равна 5%. Значит, поведение индекса S&P 500 аналогично активу, доходность которого в масштабе фунтов стерлингов равна 5 – 2,1 = 2,9%. Введя в программу DerivaGem параметры 5 = 1200, К = 1200, r = 0,05, q = 0,029, σ = 0,25, Т = 2 и выполнив 100 шагов по времени, приходим к выводу, что стоимость анализируемого опциона равна 179,83 фунтов стерлингов.

Пример из деловой практики 27.1. Парадокс Сигела

Рассмотрим две валюты, X и Y. Предположим, что процентные ставки, номинированные в этих валютах, равны r_X и r_Y и являются постоянными. Пусть 5 – количество единиц валюты Y, выплачиваемых за единицу валюты X. Как показано в главе 5, поведение обменного курса совпадает с поведением актива, доходность которого равна иностранной безрисковой процентной ставке. Следовательно, традиционный риск-нейтральный стохастический процесс, описывающий поведение переменной 5, имеет следующий вид.

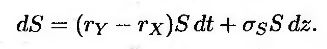
Из леммы Ито следует, что стохастический процесс, описывающий переменную 1/S, выглядит так.

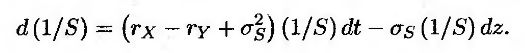
Это приводит к парадоксу Сигела, который заключается в следующем. Поскольку ожидаемая скорость роста переменной 5 в риск-нейтральном мире равна r_Y – r_X, из условия симметрии следует, что ожидаемая скорость роста переменной 1/S должна быть равной r_X – r_Y, а r_X – r_Y + σ²_S.

Чтобы понять сущность парадокса Сигела, необходимо вспомнить, что стохастический процесс, описывающий поведение переменной S при условии, что в качестве масштаба цен выбран депозитный счет денежного рынка в валюте Y, является риск-нейтральным. Этот процесс описывает поведение случайной величины 1/S, поскольку он является следствием процесса, описывающего поведение величины S. Следовательно, эта переменная также является единицей масштаба цен. Поскольку переменная 1/S представляет собой количество единиц валюты X, выплачиваемой за единицу валюты Y, то для обеспечения симметрии мы должны измерять процесс при условии, что в качестве масштаба цен выбран счет денежного рынка в валюте X. Из формулы (27.7) следует, что при изменении масштаба цен путем замены депозитного счета денежного рынка в валюте X депозитным счетом денежного рынка в валюте Y скорость роста переменной 1/5 увеличивается на ρσ_Vσ_S, где V = 1/S, а ρ – коэффициент корреляции между переменными S и 1/S. В данном случае ρ = –1 и σ_V = σ_S. Отсюда следует, что изменение масштаба цен приводит к изменению скорости роста переменной S на величину –σ²_S. Таким образом, скорость роста переменной 1/S при условии, Что в качестве масштаба цен выбран счет денежного рынка в валюте X, а не в валюте Y, описывается следующим процессом.

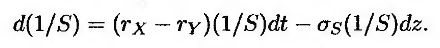
Этот процесс симметричен по отношению к стохастическому процессу, описывающему поведение переменной S. Таким образом, парадокс разрешен!