28.3. Безарбитражные модели

Недостаток моделей равновесия, описанных в предыдущих разделах, заключается в том, что они не могут автоматически учесть сегодняшнюю временную структуру. При правильном выборе параметров они могут аппроксимировать многие временные структуры, встречающиеся на практике. Однако эти аппроксимации не всегда оказываются точными, а в некоторых случаях характеризуются значительными ошибками. Большинство трейдеров этим недовольны. Они считают, что если модель не позволяет правильно оценить облигацию, то и оценкам стоимости облигационного опциона доверять не стоит. Один процент ошибки при оценке стоимости облигации может привести к 25%-ной ошибке при вычислении цены опциона.

Безарбитражная модель (non-arbitrage model) точно учитывает сегодняшнюю временную структуру процентных ставок. Таким образом, существенная разница между моделями равновесия и безарбитражными моделями заключается в следующем. В моделях равновесия сегодняшняя временная структура процентных ставок является результатом, а в безарбитражных моделях они представляют собой часть входной информации.

В моделях равновесия дрейф краткосрочной ставки (т.е. коэффициент при величине d(t), как правило, не является функцией от времени. В безарбитражных моделях этот дрейф обычно зависит от времени. Это объясняется тем, что в безарбитражных моделях форма первоначальной нулевой кривой определяет среднюю траекторию краткосрочной процентной ставки, которую она пройдет в будущем. Если нулевая кривая на отрезке от момента t₁ до t₂ круто возрастает, краткосрочная процентная ставка r на этом промежутке времени имеет положительный дрейф. Если же нулевая кривая на отрезке от момента t₁ до t₂ круто убывает, краткосрочная процентная ставка r на этом промежутке времени имеет отрицательный дрейф.

Оказывается, некоторые модели равновесия можно преобразовать в безарбитражные модели, описав дрейф краткосрочной процентной ставки с помощью функции, зависящей от времени.

Модель Хо-Ли

Первую безарбитражную модель временной структуры в 1986 году предложили Хо (Но) и Ли (Lee). Их модель представляла собой биномиальное дерево цен облигации с двумя параметрами: стандартным отклонением краткосрочной процентной ставки и рыночной стоимостью риска, связанной с краткосрочной процентной ставкой. Авторы показали, что в рамках модели для непрерывного времени стохастический процесс, описывающий поведение краткосрочной процентной ставки, имеет вид

где σ – постоянное мгновенное стандартное отклонение краткосрочной процентной ставки, a θ(t) – функция от времени, гарантирующая согласование модели с первоначальной временной структурой. Функция θ(t) определяет среднюю траекторию, которую прошла краткосрочная процентная ставка r к моменту t. Она не зависит от уровня ставки r. Интересно, что параметр Хо и Ли, оценивающий рыночную стоимость риска, связанного с колебаниями краткосрочной процентной ставки, оказывается непригодным для оценки процентных деривативов. Этот факт аналогичен тому, что рисковые предпочтения непригодны для оценки фондовых опционов.

Функцию θ(t) можно вычислить аналитически по формуле

где F(0, t) – мгновенная форвардная ставка в момент погашения облигации t, оцениваемая в нулевой момент, а индекс t означает частную производную по переменной t. Функция θ(t) приближенно равна F_t(0, t). Это значит, что среднее направление, в котором в будущем будет изменяться краткосрочная процентная ставка, приближенно равно наклону мгновенной форвардной кривой. Модель Хо-Ли продемонстрирована на рис. 28.3.

Наклон форвардной кривой определяет среднее направление, в котором краткосрочная процентная ставка изменяется в любой заданный момент времени. Кроме того, предполагается, что наклон является нормально распределенной случайной величиной.

С помощью модели Хо-Ли стоимость облигаций с нулевым купоном и европейских опционов на облигации с нулевым купоном можно вычислить по аналитическим формулам. Выражение для вычисления цены облигации с нулевым купоном в момент t по величине краткосрочной процентной ставки г имеет вид

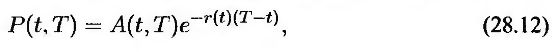
где

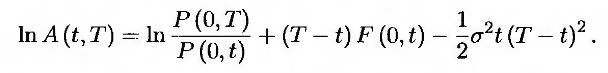
В этом равенстве нулевым моментом времени является сегодняшний день. Моменты T и t, относятся к будущему, причем Т ≥ t. Таким образом, эти формулы определяют цену облигации с нулевым купоном в будущий момент времени t по величине краткосрочной процентной ставки r и сегодняшним ценам облигаций. Последнюю величину можно вычислить с помощью сегодняшней временной структуры.

Однофакторная модель Халла-Уайта

В работе, опубликованной в 1990 году, Халл и Уайт исследовали модификации модели Васичека, позволяющие точно учесть первоначальную временную структуру. Одна из модификаций модели Васичека имеет вид

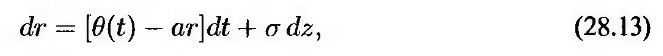
или

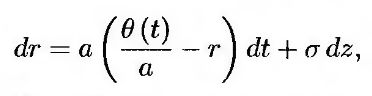
где а и a – константы. Эта модель известна как модель Халла-Уайта. С одной стороны, ее можно считать разновидностью модели Хо-Ли с возвращением к среднему со скоростью а. С другой стороны, ее можно рассматривать как модель Васичека, в которой уровень возвращения зависит от времени. В момент t краткосрочная ставка возвращается к величине θ(t)/а. Модель Хо-Ли является частным вариантом модели Халла-Уайта при а = 0.

По сложности эта модель сравнима с моделью Хо-Ли. Функцию θ(t) можно вычислить по первоначальной временно́й структуре (см. задачу 28.14):

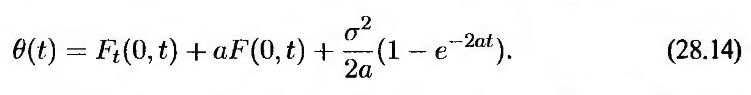
Последнее слагаемое в этой формуле, как правило, очень мало. Если отбросить его, то легко доказать, что дрейф процесса, описывающего поведение краткосрочной процентной ставки r в момент t, равен F_t(0, t) + a[F(0, t) – r]. Отсюда следует, что в среднем величина r представляет собой наклон первоначальной кривой мгновенной форвардной ставки. Если она отклоняется от этой кривой, то с течением времени возвращается назад со скоростью а. Эта модель изображена на рис. 28.4.

Цены облигаций в момент t, вычисленные по модели Халла-Уайта, определяются по формуле

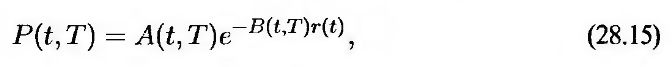
где

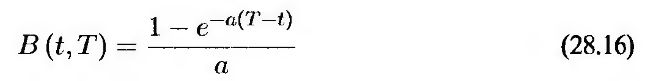
и

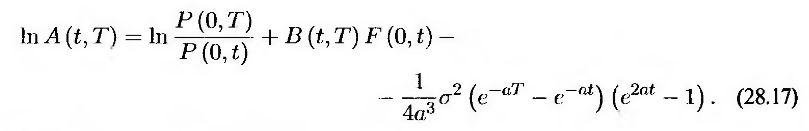
Формулы (28.15)-(28.17) определяют цену облигации с нулевым купоном в будущий момент t по краткосрочной процентной ставке в момент t и сегодняшним ценам облигаций. Последний показатель можно вычислить, используя сегодняшнюю временну́ю структуру.

Модель Блэка-Карасински

Недостаток моделей Хо-Ли и Халла-Уайта заключается в том, что краткосрочная процентная ставка r может стать отрицательной. Модель, в которой процентная ставка может принимать только положительные значения, предложили Блэк и Карасински (Karasinski):

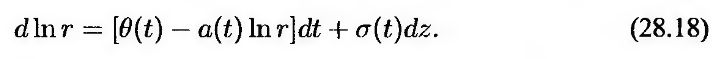
Поведения величины ln r в этой модели и величины r в модели Халла-Уайта описываются одним и тем же процессом. В то же время в моделях Хо-Ли и Халла- Уайта процентная ставка r в будущем имеет нормальное распределение, а в модели Блэка-Карасниски – логнормальное.

Модель Блэка-Карасински не так удобна с аналитической точки зрения, как модель Хо-Ли или Халла-Уайта. Например, с ее помощью невозможно вывести формулы для оценки облигаций на основе процентной ставки r.

Двухфакторная модель Халла-Уайта

Бреннан и Шварц предложили безарбитражную модель, основанную на той же идее, что и двухфакторная модель равновесия.

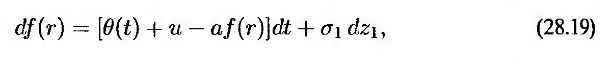
где величина u в начальный момент времени равна нулю и подчиняется стохастическому процессу

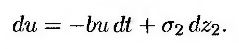
Как и в рассмотренных однофакторных моделях, параметр θ(t) выбирается так, чтобы модель была согласована с первоначальной временной структурой. Стохастическая переменная и является компонентом уровня возврата (reversion level) переменной r и сама возвращается к нулю со скоростью b. Параметры а, b, σ₁ и σ₂ являются постоянными, a dz₁ и dz₂ – винеровские процессы с мгновенной корреляцией ρ.

Эта модель предоставляет больше возможностей выбора временной структуры и волатильности, чем однофакторная. Более подробно эта модель описана в техническом замечании 14 на Web-сайте автора.