29.2. Модель рынка LIBOR

Один из недостатков модели HJM заключается в том, что она основана на мгновенных форвардных ставках, которые не поддаются непосредственному наблюдению на рынке. Кроме того, эту модель сложно калибровать с помощью финансовых инструментов, являющихся предметами активной торговли. Альтернатива была предложена в работах Брейса (Brace), Гатарека (Gatarek) и Музиелы (Musiela), Джамшидяна (Jamshidian) и Милтерсена (Miltersen), а также Сэндмана (Sandmann) и Зондермана (Sondermann). Она называется моделью рынка LIBOR (LMM – LIBOR market model) или моделью BGM (BGM – Brace-Gatarek-Musiela model) и основана на применении форвардных ставок, привычных для трейдеров.

Модель

Пусть t₀ = 0, a t₁, t₂, ... – моменты установки новых процентных ставок для опционов “кэп”, являющихся предметом торговли в настоящее время. В наиболее популярных опционах “кэп”, заключаемых в США, процентные ставки устанавливаются раз в квартал, поэтому не будет большой ошибкой считать, что t₁ = 0,25, t₂ = 0,50, t₃ = 0,75 и т.д. Пусть Δ_k = t_k+1 – t_k. Введем следующие обозначения.

F_k(t): форвардная ставка, установленная на период между моментами t_k и наблюдаемая в момент t при условии, что период начисления равен Δ_k;

m(t): индекс следующей даты установки процентной ставки по отношению к моменту t, т.е. наименьшее целое число, такое, что t ≤ t_m(t);

ζ_k(t): волатильность форвардной ставки F_k(t) в момент t;

u_k(t): волатильность цены облигации с нулевым купоном P(t, t_k) в момент t.

Для начала предположим, что в модели предусмотрен только один фактор. Как показано в разделе 25.4, в форвардных риск-нейтральных условиях относительно P(t, t_{k + 1}) стохастический процесс F_k(t) является мартингалом, а его изменение подчиняется следующему закону:

где dz – винеровский процесс.

На практике процентные деривативы удобнее всего оценивать в форвардных риск-нейтральных условиях относительно облигации, срок обращения которой истекает в момент следующей установки процентной ставки. Эти условия создают скользящий форвардный риск-нейтральный мир (rolling forward risk-neutral world). В этом случае дисконтирование от момента t_{k + 1} к моменту t_k можно осуществлять по нуль-купонной ставке, наблюдаемой в момент t_k для облигаций, срок обращения которых истекает в момент t_{k + 1}, и не интересоваться, как изменятся процентные ставки на промежутке времени между этими моментами.

В момент t скользящий форвардный риск-нейтральный мир обеспечивает форвардные риск-нейтральные условия относительно цены облигации P(t, t_m(t)). Уравнение (29.7) представляет собой процесс, которому подчиняется форвардная ставка F_k(t) в форвардных риск-нейтральных условиях относительно величины P(t, t_m(t)). Из раздела 25.7 следует, что процесс, описывающий поведение форвардной ставки F_k(t) в скользящем форвардном риск-нейтральном мире, имеет следующий вид.

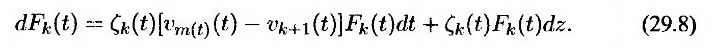
Зависимость между форвардной ставкой и ценой облигации выражается соотношением

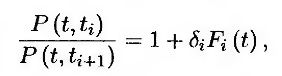
или

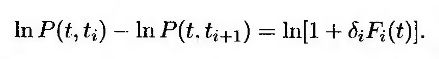
Используя лемму Иго, можно вычислить процесс, описывающий изменение левой и правой частей этого соотношения. Приравнивая коэффициенты при dz, получим следующее равенство.

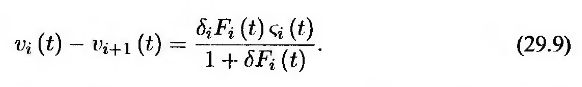
Таким образом, из формулы (29.8) следует, что процесс, описывающий изменение форвардной ставки F_k(t) в скользящем форвардном риск-нейтральном мире, выглядит так.

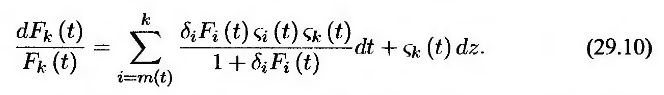
Модель HJM является частным случаем формулы (29.4). Она получается путем предельного перехода, когда величина δ_i стремится к нулю (см. задачу 29.7).

Волатильность форвардной ставки

Упростим модель, предположив, что ζ_k(t) – функция, зависящая только от общего количества периодов накопления, лежащих между следующей датой установки процентной ставки и моментом t_k. Обозначим через Λ_i значение функции ζ(t), если в этом промежутке насчитывается i периодов накопления. Это значит, что ζ_k(t) = Λ_{k – m(t)} является ступенчатой функцией.

Величину Λ_i можно (по крайней мере, теоретически) оценить с помощью волатильности, использованной для оценки кэплетов по модели Блэка (т.е. по значениям спот-волатильности, изображенным на рис. 26.3). Пусть σ_k – волатильность кэплета по Блэку, относящаяся к промежутку времени между моментами t_k и t_{k +} . Приравнивая дисперсии, получаем уравнение

Чтобы найти величину А, достаточно решить это уравнение с помощью итерационного метода.

Пример 29.1

Предположим, что все величины δ_i равны между собой, а спот-волатильности первых трех кэплетов по Блэку равны 24, 22 и 20%. Это значит, что Λ₀ = 24%. Поскольку

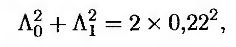
приходим к выводу, что Λ₁ = 19,80%. Кроме того,

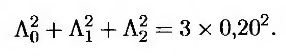
Таким образом, Λ₂ = 15,23%.

Пример 29.2

Проанализируем данные о волатильности кэплета, приведенные в табл. 29.1. Они демонстрируют “горб”, упомянутый в разделе 26.3. Величины Λ указаны во второй строке. Обратите внимание на то, что “горб”, характерный для величин Λ, выражен более ярко, чем “горб” в распределении величин σ.

Реализация модели

Модель рынка LIBOR можно реализовать с помощью метода Монте-Карло. Перепишем уравнение (29.10) относительно величин Λ.

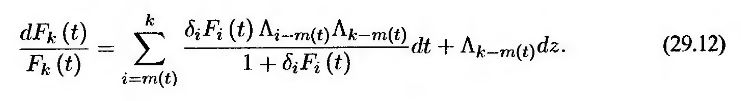
Иначе говоря,

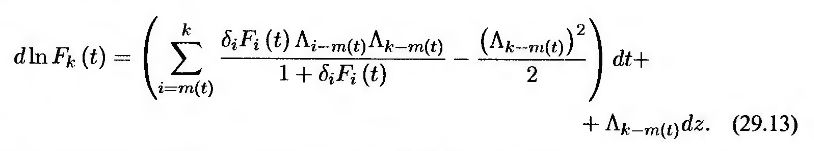
Если при вычислении дрейфа процесса lnF_k(t) предположить, что при t_j < t < t_{j + 1} выполняется условие F_i(t) = F_i(t_j), то

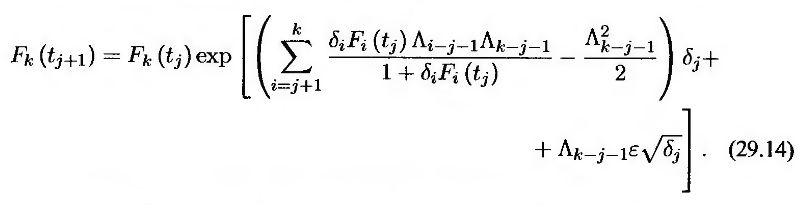
Здесь ε – случайное число, извлеченное из генеральной совокупности, имеющей нормальное распределение с нулевым математическим ожиданием и единичным стандартным отклонением.

Распространение модели на ситуации с несколькими факторами

Модель рынка LIBOR можно распространить на ситуации с несколькими независимыми факторами. Пусть р – количество факторов, а – компонент волатильности форвардной ставки F_k(t), связанный с q-м фактором. В этом случае уравнение (29.10) примет иной вид (см. задачу 29.11).

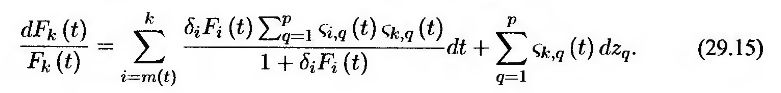
Обозначим через λ_{i, q} q-й компонент волатильности при условии, что в промежутке между датой следующей установки процентной ставки и датой прекращения форвардного контракта помещается i периодов накопления. Тогда уравнение (29.14) можно переписать следующим образом.

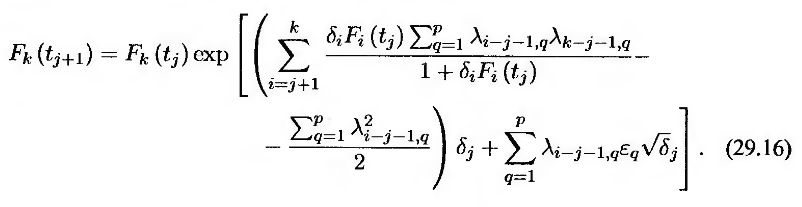
Здесь ε_q – выборочные значения, извлеченные из генеральной совокупности, имеющей нормальное распределение с нулевым математическим ожиданием и единичным стандартным отклонением.

Предположение, что на протяжении каждого периода накопления дрейф форвардной ставки остается постоянным, позволяет нам в процессе моделирования “перепрыгивать” от одной даты установки процентной ставки к другой. Это удобно, поскольку, как указывалось ранее, в скользящем форвардном риск-нейтраль- ном мире можно осуществлять дисконтирование одной даты установки процентной ставки к другой. Предположим, нам необходимо смоделировать нулевую кривую для N накопительных периодов. Каждая попытка начинается с форвардных ставок, установленных в нулевой момент времени. Они равны F₀(0), F₁ (0), ..., F_{N – 1}(0) и вычисляются по начальной нулевой кривой. Затем с помощью уравнения (29.16) вычисляются значения F₁(t₁), F₂(t₁), ..., F_{N – 1}(t₁). После этого на основе уравнения (29.16) вычисляются значения F₂(t₂), F₃(t₂), ..., F_{N – 1}(t₂). Выполнение этой процедуры продолжается до тех пор, пока не будет вычислено значение F_{N – 1}(t_{N – 1}). Обратите внимание на то, что с течением времени нулевая кривая становится короче. Например, предположим, что продолжительность каждого периода накопления равна трем месяцам, а N = 40. Начнем вычисления с десятилетней нулевой кривой. В точке, соответствующей шести годам (т.е. t₂₄), моделирование дает нам информацию о четырехлетней нулевой кривой.

Предположение о дрейфе можно проверить, оценив кэплеты на основе уравнения (29.16) и сравнив эти цены с результатами, полученными с помощью модели Блэка. Величина F_k(t_k) представляет собой реализованную ставку, установленную на период времени между моментами t_k и t_{k + 1}. Она позволяет вычислить выигрыш по кэплету в момент t_{k + 1}. Этот выигрыш пересчитывается на нулевой момент времени путем поочередного перебора периодов накопления. Стоимость кэплета равна среднему значению всех дисконтированных выигрышей. Таким образом, оценка опционов “кэп” с помощью метода Монте-Карло незначительно отличается от цены, определенной по модели Блэка. Это утверждение остается справедливым даже в том случае, когда период накопления достигает одного года, а для вычисления используется очень большое количество попыток. Это значит, что предположение о постоянности дрейфа в большинстве ситуаций является вполне безопасным.

Опционы “храповой кэп”, “жесткий кэп” и “гибкий кэп”

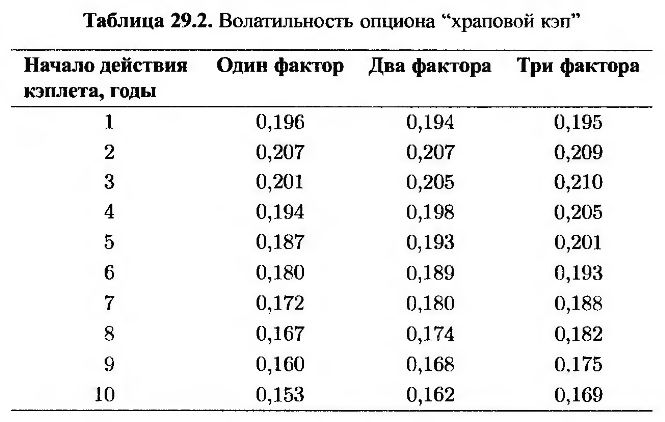
Модель рынка LIBOR можно использовать для оценки некоторых типов нестандартных опционов. Рассмотрим, в частности, опционы “храповой кэп” (ratchet cap) и “жесткий кэп” (sticky cap). Это позволит нам продемонстрировать правила вычисления предельного уровня для каждого кэплета. В опционе “храповой кэп” этот уровень равен сумме ставки LIBOR и спрэда. В опционе “жесткий кэп” он равен сумме предыдущего предельного уровня и спрэда. Предположим, что предельная ставка в момент t_j равна K_j, ставка LIBOR в момент t_j равна R_j, а спрэд равен ς. В опционе “храповой кэп” K_{j + 1} = R_j + ς. В опционе “жесткий кэп” K_{j + 1} = min(R_j, K_j) + ς.

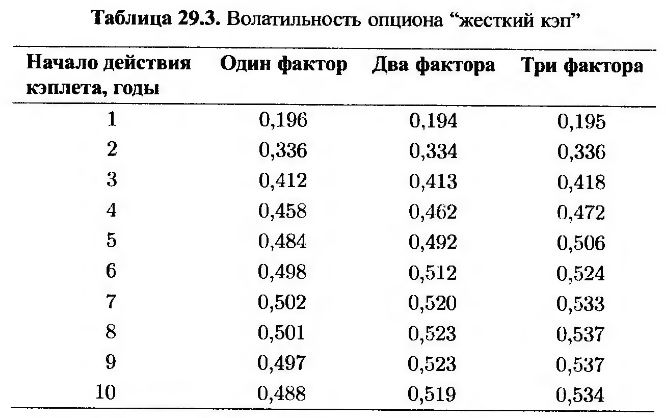
В табл. 29.2 и 29.3 приведены результаты вычислений волатильности опционов “храповой кэп” и “жесткий кэп” модели рынка LIBOR с одним, двумя и тремя факторами. Основная сумма равна 100 долл. Предполагается, что временная структура является горизонтальной и проходит на уровне 5% годовых, а волатильности кэплетов приведены в табл. 29.1. Процентная ставка устанавливается ежегодно. Спрэд равен 25 базисным пунктам. В табл. 29.2 и 29.3 демонстрируется расщепление волатильности на компоненты в двух- и трехфакторных моделях. Приведенные результаты получены путем 100000 попыток моделирования по методу Монте-Карло с помощью метода антитетической переменной, описанного в разделе 18.7. Стандартная ошибка каждой цены равна приблизительно 0,001.

Еще одним типом нестандартных опционов является опцион “гибкий кэп” (flexi cap). Он похож на обычный опцион “кэп”, за исключением того, что в нем существует ограничение на общее количество исполняемых кэплетов. Рассмотрим опцион “гибкий кэп” с ежегодными выплатами, если основная сумма равна 100 долл., временная структура является горизонтальной и проходит на уровне 5%, а волатильности кэплетов приведены в табл. 29.1, 29.4 и 29.5. Предположим, опцион “гибкий кэп” содержит не более пяти кэплетов “с выигрышем”. В ситуациях с одним, двумя и тремя факторами цены опциона “гибкий кэп”, вычисленные по модели рынка LIBOR, равны 3,43, 3,58 и 3,61. (Другие разновидности опциона “гибкий кэп” рассмотрены в задаче 24.17.)

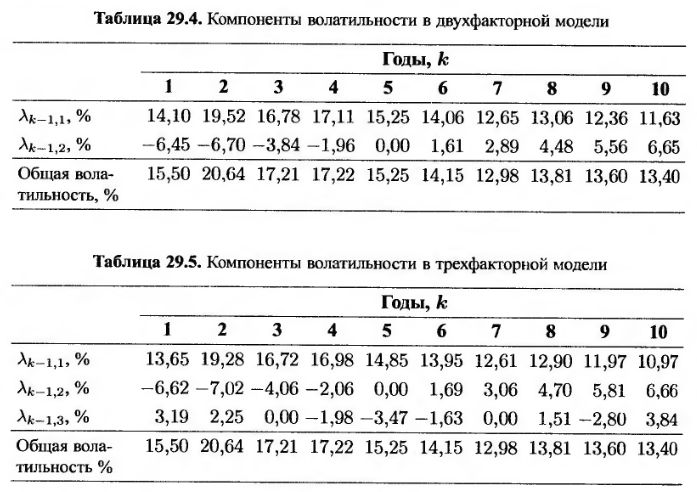
Оценка стоимости обычных опционов “кэп” зависит только от общей волатильности и не зависит от количества факторов. Это объясняется тем, что на цену обычного кэплета влияет только поведение форвардной ставки. Цены кэплетов в нестандартных финансовых инструментах, проанализированных нами, отличаются тем, что они зависят от совместного распределения вероятных значений нескольких форвардных ставок. В результате оказывается, что цены таких опционов определяются количеством учтенных факторов.

Оценка европейских свопционов

Как показано в работе Халла и Уайта, существуют аналитические формулы, позволяющие приближенно вычислить стоимость европейских свопционов с помощью модели рынка LIBOR. Пусть T₀ – срок действия свопциона, а выплаты по свопу осуществляются в моменты Т₁, Т₂, ..., T_N. Введем обозначение: τ = T_{i + 1} – T_j. Из уравнения (25.23) следует, что ставка свопа в момент t равна

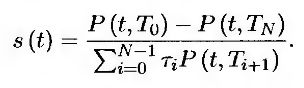
Кроме того, если 1 ≤ i ≤ N, то

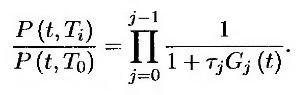
Здесь Gj(t) – форвардная ставка в момент t, установленная на период времени между моментами T_j и T_{j – 1}. Эти два уравнения определяют зависимость между функциями ς(t) и G_j(t). Применяя лемму Ито (см. задачу 29.12), приходим к выводу, что дисперсия V(t) ставки свопа ς(t) равна

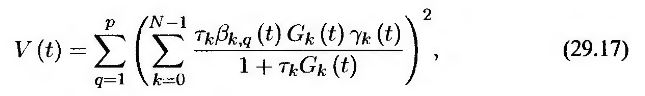
где

a Ξ_{j, q}(t) – q-й компонент волатильности функции G_j(t). При вычислении функции V(t) для всех значений j и t можно положить G_j(t) = G_j(0). Волатильность свопа, подставляемая в стандартную модель для оценки свопциона, равна

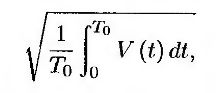
или

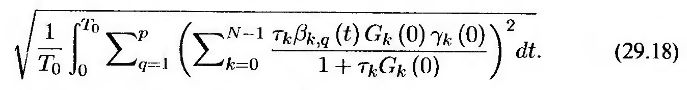
Если длина периода накопления в рамках свопа, лежащего в основе свопциона, равна длине периода накопления в рамках опциона “кэп”, то Ξ_{j, q}(t) представляет собой q-й компонент волатильности форвардной ставки в опционе “кэп”, срок действия которого истекает в момент T_k – t. Этот факт легко обнаружить, анализируя табл. 29.5.

Длины периодов накопления в рамках свопов, на основе которых брокеры устанавливают котировочные цены европейских свопционов, не всегда совпадают с длинами периодов накопления в рамках опционов “кэп” и “фло”, лежащих в основе соответствующих брокерских котировок. Например, в США процентные ставки по опционам “кэп” и “фло” устанавливаются ежеквартально, а по европейским свопционам соответствующие ставки устанавливаются только раз в полгода. К счастью, методы оценки европейских свопционов можно распространить на ситуации, в которых каждый период накопления в рамках свопа содержит М подынтервалов, которые могут быть периодами накопления в рамках обычных опционов “кэп”. Обозначим через τ_{j, m} продолжительность m-го подынтервала в j-м периоде накопления, т.е.

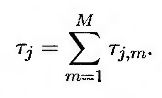
Пусть G_{j, m}(t) – форвардная ставка, наблюдаемая в момент t для периода накопления продолжительностью τ_{j, m}. Поскольку

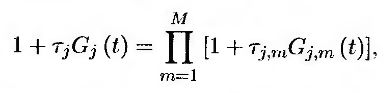
можно модифицировать анализ, проведенный при выводе уравнения (29.18), так, чтобы волатильность ставки свопа ς(t) выражалась через волатильность форвардной ставки G_{j, m}(t), а не через волатильность форвардной ставки G_j(t). Волатильность свопа, подставляемая в стандартную модель рынка при оценке свопциона, должна иметь следующий вид (см. задачу 29.13).

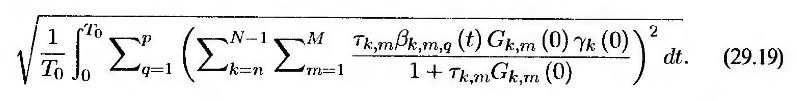
Здесь β_{j, m, q}(t) – q-й компонент волатильности форвардной ставки G_{j, m}(t). Одновременно он является q-м компонентом волатильности форвардной ставки в опционе “кэп”, если срок действия этого опциона истекает в промежутке между моментом t и началом т-го подынтервала на протяжении периода накопления по свопу (T_j,T_{j + 1}).

Выражения для волатильности свопа в формулах (29.19) и (29.19) основаны на предположении, что G_j(t) = G_j(0) и G_{j, m}(t) = G_{j, m}(0). Халл и Уайт сравнили цены европейских свопционов, вычисленные по формулам (29.19) и (29.19), с ценами, определенными с помощью моделирования по методу Монте -Карло, и выяснили, что они очень близки. Следовательно, проведя калибровку модели рынка LIBOR, с помощью формул (29.19) и (29.19) можно легко и просто вычислить стоимость европейских свопционов. На основании этих расчетов аналитики могут определить, не являются ли европейские свопционы недооцененными или переоцененными по сравнению с опционами “кэп”. Как будет показано ниже, эти результаты можно также использовать при калибровке модели, предназначенной для вычисления рыночных цен свопционов.

Калибровка модели

Для калибровки модели рынка LIBOR необходимо определить величины Λ_j и выяснить, как они раскладываются на компоненты λ_{j, q}. Для этого обычно используется метод главных компонентов, описанный в разделе 18.9. Соответствующая модель имеет вид

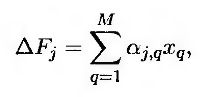
где М – общее количество факторов, ΔF_j – изменение форвардной ставки в рамках форвардного контракта, истекающего через j периодов накопления, α_{j, q} – факторная нагрузка q-го фактора (factor loading) при j-й форвардной ставке, x_q – значение q-го фактора (factor score), и

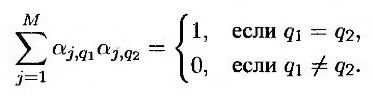
Обозначим через τ_q стандартное отклонение значения q-го фактора. Если количество факторов в модели рынка LIBOR, р, равно общему количеству факторов М, то выполняется равенство

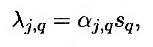
где 1 ≤ j, q ≤ М. Если р < М, то величину необходимо масштабировать так, чтобы выполнялось равенство

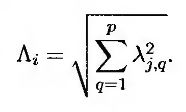
Следовательно, величину λ_{j, q} необходимо выбрать следующим образом.

Для определения величины Λ, согласованной с ценами кэплетов, можно использовать формулу (29.11). Однако на практике она обычно не применяется, поскольку часто приводит к сильным колебаниям значений Λ. Кроме того, хотя модель рынка LIBOR по определению согласована с ценами кэплетов, аналитики иногда предпочитают калибровать ее с помощью европейских свопционов.

Наиболее распространенная процедура калибровки модели рынка LIBOR напоминает процедуру, описанную в разделе 28.8 при описании калибровки однофакторной модели. Пусть U_i – рыночная цена i-го калибровочного инструмента, a V_i – его цена, вычисленная по модели. Выберем параметры Λ так, чтобы они минимизировали функцию

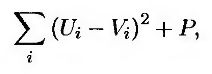
где Р – штрафная функция, обеспечивающая “хорошее поведение” параметров Λ. Как и в разделе 28.8, представим функцию Р в следующем виде.

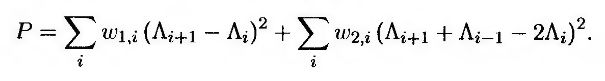
Если в качестве калибровочных инструментов выбраны европейские свопционы, то для минимизации целевой функции на основе формул (29.18) и (29.19) можно использовать процедуру Левенберга-Маркварта. Для определения параметров λ через параметры Λ используется формула (29.20).

Асимметрия волатильности

Брокеры устанавливают котировочные цены как для опционов “без проигрыша”, так и для остальных. На некоторых рынках наблюдается асимметрия волатильности, т.е. котируемая волатильность (по Блэку) опционов “кэп” и “фло” является убывающей функцией от цены исполнения. Для отражения этого факта используется модель CEV (см. раздел 20.1), имеющая следующий вид.

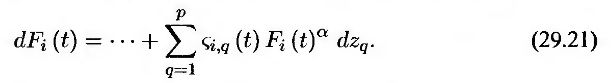
Здесь α – константа (0 < α < 1). Оказывается, эта модель мало отличается от логнормальной, а опционы “кэп” и “фло” можно оценить с помощью аналитических формул, используя интегральное нецентральное χ²-распределение. Это напоминает аналитические подходы к вычислению цен европейских свопционов.

Бермудские свопционы

Одними из популярных процентных деривативов являются бермудские свопционы (Bermudan swap options), допускающие досрочное исполнение в заранее определенные даты выплат по базовому свопу. Бермудские свопционы трудно оценивать, используя модель рынка LIBOR, поскольку она опирается на моделирование по методу Монте-Карло, что затрудняет определение целесообразности их досрочного исполнения. К счастью, эту проблему можно решить с помощью процедуры, описанной в разделе 24.7. Лонгстафф (Longstaff) и Шварц предложили для оценки бермудских свопционов с большим количеством факторов применять метод наименьших квадратов. Эта модель основана на предположении, что стоимость отказа от досрочного исполнения свопциона в определенную дату выплаты представляет собой полином, зависящий от значений факторов. Андерсен показал, что для реализации этой модели можно применить метод определения оптимальных границ досрочного исполнения (optimal early exercise boundary approach). Он провел большое количество экспериментов, в которых предполагалось, что решение о досрочном исполнении зависит только от действительной стоимости опциона. Большинство трейдеров оценивают бермудские опционы с помощью однофакторной безарбитражной модели, описанной в главе 28. Точность этой модели до сих пор остается под вопросом.