|
Логнормальное распределение лишь приближенно соответствует реальным движениям рыночных цен. Фиксируя его параметры Mean и о, мы за счет усреднения сильно огрубляем информацию, содержащуюся в исторических ценовых рядах. Естественным выглядит предположение о том, что будущее должно быть похоже на прошлое, и максимальный перенос информации о движении цены из известного нам прошлого в предполагаемое будущее. Эту цель преследует построение эмпирического распределения.
Для каждой акции мы собираем вместе реально произошедшие в истории ценовые движения и предполагаем, что в прогнозируемом будущем движения могут реализоваться с вероятностью, соответствующей реальной частоте их наблюдения в прошлом.
Формальное построение эмпирического распределения делается следующим образом. Через Т0 обозначим текущий момент времени, а через Т– тот момент в будущем, для которого мы будем строить эмпирическое распределение цены базового актива. Разницу τ = Т– Т0, τ > 0 назовем горизонтом прогноза.


Будем считать, что движение цены является случайной величиной. Наше главное предположение заключается в том, что ее распределение можно построить на наблюдениях ее реализаций в прошлом. Размер истории цен, которая служит материалом для построения распределения, будем называть горизонтом истории эмпирического распределения и обозначим через I (причем, τ> т). Чем больше горизонт истории, тем больше статистического материала оказывается в нашем распоряжении. Но в силу нестационарности рыночных закономерностей старые исторические данные могут давать неправильную информацию о том, что происходит в настоящее время. Поэтому выбор наилучшего горизонта истории L представляет собой важную задачу, аналогичную определению оптимального значения N, служащего параметром для расчета HV для логнормального распределения.
Задав значения горизонтов τ и L, рассмотрим относительные приращения цен р(t) = С(t + τ)/С(0 для всех моментов г выбранной истории, не позволяя себе «заглядывать в будущее» по отношению к Г0: t = T0-L + 1, T0-L + 2,..., Т0-τ. Таким образом, мы получим L-τ наблюдений приращений цены. Умножая текущую цену С(Г0) на каждое из приращений цены, мы получим L-τ вариантов будущей цены:
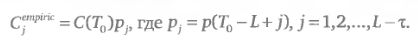
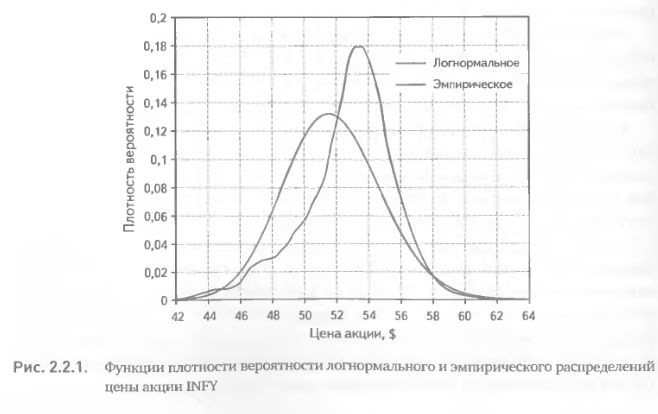
Полученный набор значений цены можно использовать разными способами. Самый наглядный – это построить функцию плотности вероятности будущего распределения цены Empiric(x) на основе гистограммы полученных значений. Для сравнения построим плотности логнормального и эмпирического распределений для цены акции INFY. Эта акция 05 апреля 2007 г. на закрытии торгов стоила $ 51,83. Ее историческая волатильность, рассчитанная по формуле 2.1.2 на истории 120 последних торговых дней (N= 120), составила 28%. Принимая значение параметра Mean равным текущей цене акции, получаем логнормальное распределение задаваемое формулой 2.1.1 (рис. 2.2.1). Дня эмпирического распределения горизонт прогноза τ определен расстоянием до даты экспирации 21 апреля 2007 г. и составляет 11 торговых дней. Горизонт истории I взят равным 250 торговым дням. На рис. 2.2.1 хорошо видно, что эмпирическое распределение по сравнению с логнормальным имеет смещение среднего и максимального значений вправо, более высокую и узкую среднюю часть и немного более толстые «хвосты».
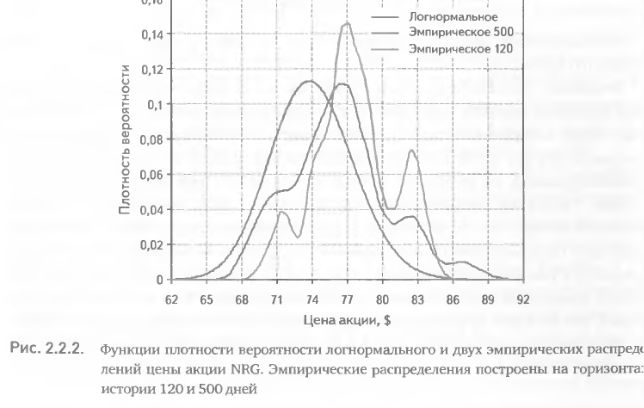
Обычно расхождение двух распределений тем больше, чем меньше горизонт используемой истории. На рис. 2.2.2 изображено логнормальное и два эмпирических распределения для акции NRG на 05 апреля 2007 г. для горизонта прогноз: соответствующего дате экспирации 21 апреля 2007 г. Логнормальное распределение использует историческую 120-дневную волатильность 22,86% и текущую цену акции $ 73,88. Плотности эмпирических распределений построены на 12( и 500-дневной истории. На рис. 2.2.2 хорошо видно: чем короче горизонт истории, тем более причудливую форму принимает эмпирическое распределение и тем сильнее оно отличается от логнормального. Смещение пиков распределений вправо отражает растущий тренд акции. Эмпирическое распределение в отличие от логнормального, хорошо отражает тренды и прошлые сильные движения цены. Рисунок 2.2.2 наглядно демонстрирует, что выбор значения параметра «горизонт истории» I имеет большое влияние на форму эмпирического распределения. Как следствие, I является определяющим параметром при расчете значений критериев, основанных на этом распределении.
|