2.2.5. Модификации эмпирического распределения

На первый взгляд эмпирическое распределение должно работать лучше любого другого распределения, поскольку именно оно в точности повторяет движения цены, действительно произошедшие в прошлом. Однако здесь как раз и таится подвох. Статистики рынка, как правило, не являются стационарными. То, что происходило ранее, не всегда повторяется. Тренды и боковые движения сменяют друг друга, а волатильные периоды чередуются со спокойными без какой-либо закономерной периодичности. Поэтому эмпирическое распределение как простая совокупность прошлых наблюдений не всегда может быть наилучшим вариантом вероятностного прогноза. Существует несколько способов модификации эмпирического распределения. Два из них мы опишем ниже.

Замена параметра «горизонт истории» весовой функцией

Один из способов модификации эмпирического распределения представляет собой введение весового усреднения прошлых ценовых движений. Это достигается назначением больших весовых коэффициентов тем наблюдениям, которые находятся ближе к сегодняшнему дню. Тогда вместо формул 2.2.2 и 2.2.4 получатся выражения:

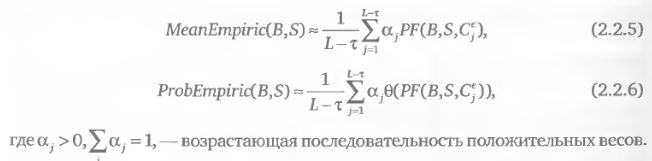
Пользуясь формулами 2.2.5 и 2.2.6, можно рассчитывать значения критериев таким образом, чтобы недавние ценовые движения оказывали большее влияние на конечный результат, чем более отдаленные во времени изменения цен. Фактически это означает постепенное «забывание» старых данных. Можно придать функции a(j), задающей значения весов {α_j}, любой вид по нашему выбору– она может быть линейной (с равномерно убывающими во времени весовыми коэффициентами), экспоненциальной или любой другой. Выбор конкретных параметров данной функции может заменить собой оптимизацию такого важного параметра эмпирического распределения, как горизонт истории. Достигается это следующим образом – горизонт истории принимается максимально большим (например, свыше нескольких лет или же вся имеющаяся в наличии база исторических данных). В такой ситуации оптимизация L подменяется выбором формы «забывания старых данных» за счет введения в модель оптимальной формулы и параметров функции a(j).

На первый взгляд применение формул 2.2.5 и 2.2.6 заменяет одну сложную проблему (оптимизацию L) другой – выбором формулы и метода оптимизации параметров функции а. На самом деле это не так. Для оптимизации L мы не обладаем никакими объективными критериями принятия решения, кроме настройки на прошлые ценовые данные, которая может оказаться простой подгонкой, приводящей к печальным последствиям переоптимизации. С другой стороны, выбор функции a(j) может быть осознанным и объективно отражать представления инвестора о цикличности и повторяемости рыночных процессов. Безусловно, выбор данной функции является сложной задачей, к методам решения которой мы вернемся в нашей следующей книге.

Симметризация эмпирического распределения

Как показывает практика, весьма полезной может оказаться другая форма модификации эмпирического распределения – его симметризация. Суть симметризации заключается в добавлении в выборку наблюдений вместе с каждым отношением цен p (t) = C(t + τ)/C(t) его обратного значения p^-1 (t) = C(t)/C(t +τ). Данная процедура фактически обогащает исходную информацию, перенося в будущее не только то, что состоялось в прошлом, но и гипотетические противоположные ценовые движения. Этим способом реализуются два вполне правдоподобных рассуждения. Во-первых, мы отказываемся от гипотезы сохранения направленности ценовых движений (напомним, что эмпирическое распределение отражает превалировавшие в прошлом тренды). Известно, что все тренды рано или поздно сменяются контртрендами или коррекциями. При этом не существует надежных инструментов, позволяющих достоверно установить вероятность продолжения или прекращения тренда. Во-вторых, что тоже вполне правдоподобно, возможные противоположные движения цен, скорей всего, будут обладать характеристиками, близкими к предшествующим движениям.

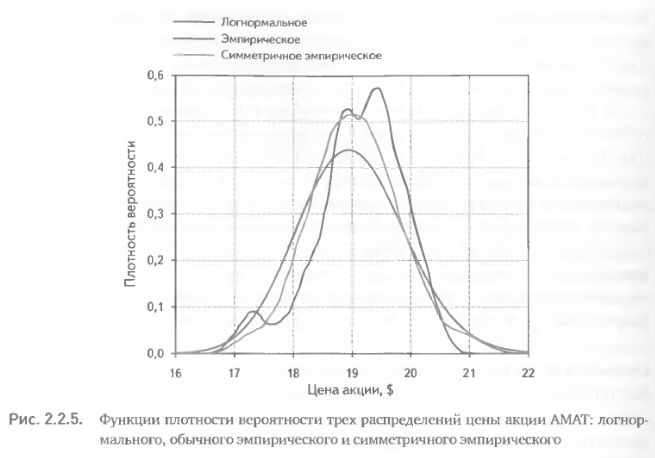
Увидеть, насколько силен эффект симметризации эмпирического распределения, можно на рис. 2.2.5. На нем одновременно изображены три распределения для акции АМАТ на 1 июня 2007 г., когда она торговалась по цене $ 19,34, а 120-дневная историческая волатильность составляла 23,28%. Все распределения рассчитаны как вероятностные прогнозы на ближайшую дату экспирации 16 июня 2007 г. Эмпирические распределения строились по 120-дневной истории. Симметризация не только сглаживает функцию плотности вероятности эмпирического распределения, но и устраняет перекошенность при сохранении индивидуальных особенностей и расхождений с логнормальным распределением (рис. 2.2.5).

После проведения процедуры симметризации очевидным образом получаются два новых критерия, аналогичных получаемым по формулам 2.2.1 и 2.2.2. Функцию плотности нового симметричного эмпирического распределения обозначим через SymEmpiric(x). Тогда критерий «математического ожидания прибыли на основе симметричного эмпирического распределения» имеет вид:

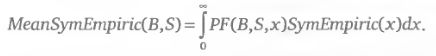
А критерий «вероятность получения прибыли на основе симметричного эмпирического распределения» выглядит как:

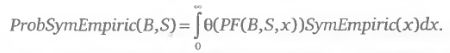
Формулы для упрощенного практического расчета критериев аналогичны выражениям 2.2.2 и 2.2.4. Применив их и используя описанный выше алгоритм расчета, вычислим значения критериев для уже рассмотренного нами примера короткого стрэнгла по акции YHOO. Фактически мы должны к каждому р_j, приведенному в табл. 2.2.1, добавить еще и обратное ему значение. Например, для p_j = 1,02 получим р^-1_j = 1/1,02 = 0,98. Соответственно G^emp_j = 0,98 х 28,38 = 27,81, а платежная функция в этой точке будет равна PF_j = 0,55. Усреднив 148 значений платежной функции (74 значения приведенных в табл. 2.2.1 плюс 74 расчетных значения) и 148 значений те функции, получим следующие значения критериев: MeanSymEmpiric(B, S) 0,37 и ProbSymEmpiric(B, S) = 0,45. Как видим, в данном случае симметричное распределение дало худшие значения для обоих критериев по сравнению с обычным эмпирическим распределением. В других случаях возможна обратная ситуация – симметричное распределение дает лучшие показатели. Так или иначе опыт показывает, что два критерия не дублируют, а дополняют друг друга.