|
Чтобы оценить, влияет ли корреляция между критериями на прибыльность комбинаций, отобранных на основе их показателей, построим зависимость средней прибыли комбинаций, отобранных по методу Парето (оптимальное множество состоит из двадцати слоев), от коэффициентов корреляции (использовались все 55 пар критериев, приведенных в табл. 8.2.1). Для большей достоверности результатов мы решили не ограничиваться одной датой, а провели анализ трех дат, относящихся к первым месяцам 2007 г. (открытие позиций в первый рабочий день месяца–3 января, 1 февраля и 1 марта). Доходность рассчитывалась для каждой комбинации на дату истечения опционов и выражалась как процент от маржевых требований на дату открытия позиции.


Январские и мартовские позиции не показали достоверной связи между исследуемыми величинами (рис. 8.3.1), зато для февраля была установлена положительная, статистически значимая зависимость между прибылью и корреляцией (уровень значимости р < 0.01). На рис. 8.3.1 видно, что чем выше корреляция между критериями, тем выше средняя прибыль комбинаций. Такой результат противоречит нашим интуитивным представлениям – ведь сильная корреляция означает «схожесть» критериев.
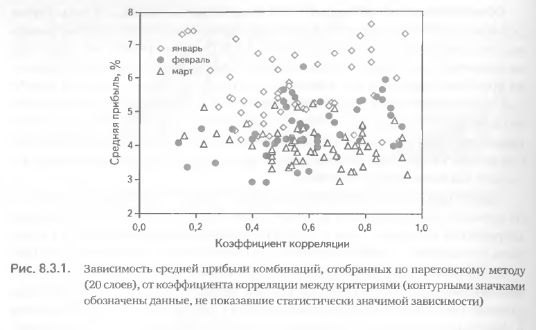
А их схожесть, в свою очередь, означает, что использование дополнительных критериев существенно не улучшает нашу способность отбирать лучшие комбинации. В предельном случае приближение коэффициента корреляции к единице ведет к полному совпадению значений критериев, а многокритериальный отбор сводится к монокритериальному.
Это противоречие вынуждает нас глубже разобраться в природе установленной положительной зависимости – ведь если мы не найдем логичное объяснение обнаруженного феномена, то лучшее, что можно сделать, – это отказаться от многокритериального отбора и работать на основе единственного критерия [либо использовать сильно коррелирующие критерии).
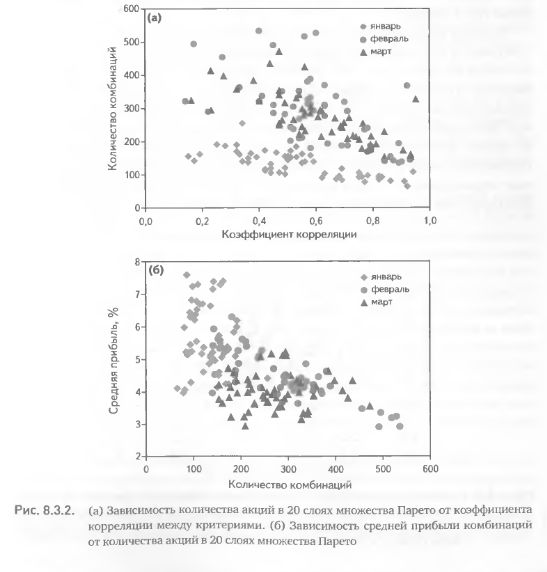
Забегая вперед, скажем, что обнаруженный парадокс легко объясняется, если проанализировать опосредованное влияние корреляции на среднюю прибыль через количество акций, попадающих в множество Парето. Рисунок 8.3.2 (а) наглядно демонстрирует: чем больше корреляция между критериями, тем меньше акций попадает в множество Парето. Результат этот неудивителен: чем шире облако точек (т. е. меньше корреляция) в двумерном пространстве, аналогичном приведенному на рис. 7.2.1, тем больше их отсекается каждым паретовским слоем (в предельном случае, если корреляция стремится к 1, то количество Парето-оптимальных точек не превышает числа используемых слоев). С другой стороны, чем больше точек попадает в отобранное множество, тем меньше их средняя прибыль (рис. 8.3.2 (б)). Этот результат также не является неожиданным: чем больше отбирается точек, тем хуже средние значения их критериев (напомним, что это объяснение мы уже использовали для зависимостей, представленных на рис. 7.2.2). Более того, такой результат закономерен, если наши критерии действительно работают. Итак, суммируя эти два анализа, можно заключить, что высокая корреляция между критериями приводит к сокращению числа комбинаций, попадающих в множество Парето, а это, в свою очередь, повышает среднюю прибьль за счет отбора только самых лучших по критериям элементов. (Заметим, что при этом снижается диверсификация портфеля).
Таким образом, мы объяснили опосредованное влияние корреляции на прибыль. Вместе с тем интуиция подсказывает, что должно существовать и прямое воздействие корреляции. Мы полагаем, что с уменьшением взаимозависимости критериев прибьль должна расти, поскольку критерии не дублируют друг друга и отбираемое множество комбинаций использует преимущества двух (или более) разных оценочных систем.
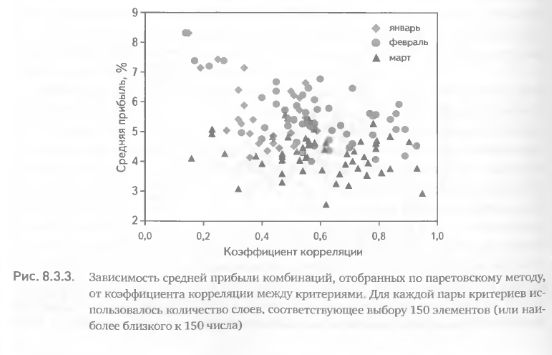
Чтобы доказать это, построим зависимость, аналогичную показанной на рис. 8.3.1, но на этот раз будем использовать не 20 паретовских слоев, а для каждой пары критериев возьмем такое количество слоев, которое создает оптимальное множество из 150 элементов (или наиболее близкого к 150 числа). Действительно, устранение влияния количества комбинаций полностью меняет результат. Положительная зависимость прибыли от корреляции (рис. 8.3.1) превращается в отрицательную (рис. 8.3.3). Для всех трех исследуемых месяцев получена обратная зависимость средней прибыли от коэффициента корреляции, и для двух из них эта зависимость статистически значима. Таким образом, когда опосредованное (через количество акций) влияние корреляции на прибыль нейтрализуется, проявляется истинная природа зависимости этих двух величин. Мы видим, что в общем случае прибыльность комбинаций выше для слабо коррелирующих пар критериев.
Пример приведенного здесь анализа весьма показателен. Установив некую зависимость (высокая корреляция критериев дает лучшую прибыль, рис. 8.3.1), мы могли бы начать использовать ее на практике, отбирая для торговли комбинации по сильно коррелирующим критериям. Такой шаг был бы весьма опрометчивым. Нельзя использовать никакие, даже достоверно установленные, закономерности, не разобравшись в их природе. Причин тому несколько. Во-первых, фактор, определенный как влияющий на якобы зависящую от него переменную, может оказаться зависимым от третьей, не участвовавшей в анализе переменной (которая и повлияла на исследуемую зависимую величину). Во-вторых (как в приведенном выше примере), влияющий фактор (корреляция) может воздействовать на зависимую переменную (прибыль) как прямо, так и косвенно через другие, зависящие от него факторы (количество отбираемых комбинаций).
В результате эффект опосредованного влияния может «зашумить» результат, а то и вовсе изменить его на противоположный. Таким образом, прежде чем внедрять в практику установленную закономерность, необходимо убедиться в истинности полученного эффекта. В противном случае результат может оказаться противоположным ожидаемому–не улучшение, а ухудшение прибыльности торговли.
|