|
Биноминальная модель определения цены опциона была разработана Дж. Коксом (Cox) и др. (1979). Основное допущение этой модели состоит в том, что рынок опционов является эффективным, т.е. спекулянты не могут получить чрезмерно большую прибыль от комбинаций с одновременной покупкой и продажей опционов и базисных инструментов.


Если известны цена базисного инструмента, риск последнего (т.е. вероятность изменения его цены в ту или иную сторону) и безрисковая процентная ставка, то можно рассчитать цену опциона с заданным сроком истечения. Ниже приводится в качестве примера простая биноминальная модель определения цены опциона колл для одного периода на товар с текущей ценой 20 ф. ст. за единицу. Сделаны следующие допущения:
1) Цена единицы товара S = 20 ф. ст.
2) Вероятность движения цены товара вверх q = 0,5 и вниз –q = 0,5.
3) Движение цены товара будет состоять из одного периода, или «шага». При направлении «вверх» мультипликативное движение цены u = 1,2. При направлении «вниз» мультипликативное движение d = 0,67.
4) r = 1,1 (1 + безрисковая процентная ставка).
После одного периода цена товара станет равной uS с вероятностью q или dS с вероятностью (1 – q). Следовательно, имеется вероятность 50 : 50, что цена поднимется до 1,2 x 20 = 24 ф. ст., и такая же вероятность, что цена опустится до 0,67 х 20 = 13,40 ф. ст. Рассмотрим опцион колл на товар с ценой исполнения X = 21 ф. ст. Выплата покупателю опциона с такой ценой исполнения и в зависимости от возможных движений цены будет следующей:
uS = 24 ф. ст.
dS = 13,40 ф. ст.
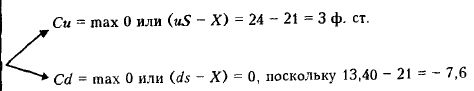
Таким образом, в случае движения цены вверх для каждого опциона колл на одну единицу товара с ценой исполнения 21 ф. ст. цена составит 3 ф. ст. В случае движения цены вниз для каждого опциона колл на одну единицу товара с ценой исполнения 21 ф. ст. цена будет равна нулю.
Какова приемлемая цена опциона колл на одну единицу товара с сегодняшней ценой исполнения 21 ф. ст.? Рассмотрим безрисковый портфель из одной единицы товара и опционов колл на m единиц этого товара. Выплата будет следующей:
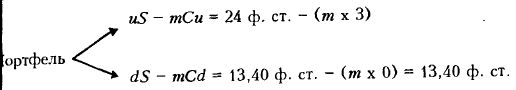
При движении цены вверх выручка от продажи единицы товара составляет 24 ф. ст., но теряется 3 ф. ст. на каждом исполнении опциона колл. При движении цены вниз выручка от продажи единицы товара составляет 13,40 ф. ст., а mCd = 0, поскольку опцион не исполняется. Для безрискового портфеля выплата при движении цены вверх должна быть равна выплате при ее движении вниз, т.к. направление движения цен не оказывает влияния на портфель.
Таким образом,
uS – mCd = dS – mCd,
uS – dS = mCu – mCd,
откуда
S(u – d) = m(Cu – Cd),
так что
m = S(u – d)/(Cu – Cd).
Подставляя значения из вышеприведенного примера:
m = 20(1,2 – 0,67)/(3 – 0),
получаем m = 3,53, т.е. безрисковый портфель состоит из одной единицы товара и 3,53 опциона колл.
Поскольку портфель был сформирован как безрисковый, текущая величина портфеля, умноженная на (1 + безрисковая процентная ставки), должна быть равной выплате в конце рассматриваемого периода. Если бы это не имело места, то существовала бы возможность арбитража между опционом, хеджированным портфелем и безрисковой процентной ставкой. Теперь можно определить текущую цену опциона колл на одну единицу товара путем сравнения хеджируемой комбинации товара и опционов колл и инвестициями в безрисковые активы. Если c – цена одного опциона колл на одну единицу товара, то текущая величина портфеля равна (S – mc), поскольку цена одной единицы товара равна S, и имеются m опционов, каждый из которых стоит ?
Следовательно,
r(S – mc) = uS – mCu,
тогда
S – mc = (uS – mCu)/r,
так что
mc = S – [(uS – mCu)/r]
и
c = {S – [(uS – mCu)/r]}/m.
Подставляя, как и раньше, значения, имеем:
c = {20 – [(24 – 3,53 x 3)/1,1]}/3,53.
Отсюда
c = 2,2147.
В вышеприведенном примере безрисковый портфель для одношагового движения цены содержал бы:
• одну единицу товара = 20 ф. ст.
• опционы колл, выписанные на 3,53 единицы товара с ценой исполнения 21 ф. ст., которые продавались бы по цене 2,21 ф. ст. за единицу товара.
Первоначальная цена портфеля = 20 – (3,53 х 2,2147) = 12,1821
Окончательная цена портфеля = 13,40
13,40/12,1821 = 1,1;
r = 1,1.
Коэффициент хеджирования при использовании биноминальной модели определения цены
Пусть m – число опционов колл, требуемое для формирования безрискового портфеля.
Коэффициент хеджирования (отношение стоимости базисного товара к стоимости опционов, использованных для формирования безрискового портфеля, содержащего выписанные опционы и купленный товар) = 1/m, или дельта.
|