|
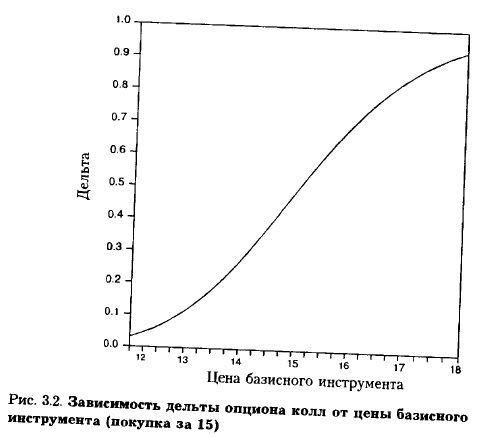
Коэффициент хеджирования дельта уже рассматривался выше в одношаговой биноминальной модели. В модели Блэка–Шолеса дельта равна N(d1), которая является мерой чувствительности, скоростью изменения премии опциона относительно цены базисного инструмента. Дельта изменяется от 0 до 1 и приблизительно равна 0,5 для опционов «с проигрышем». Поскольку для опционов «с большим проигрышем» дельта находится в своем минимуме, то такие опционы демонстрируют самую низкую чувствительность премии к изменению цены базисного инструмента (рис. 3.2).


Уменьшение волатильности со временем вызовет снижение цены опциона. Если хеджер придерживается точки зрения, что волатильность уменьшается со временем, то подходящей стратегией будет продажа опционов. Стратегии операций, основанные на продаже опционов, работают лучше в случае опционов «с проигрышем», а степень эффективности может быть повышена благодаря недостаточной чувствительности к цене базисного инструмента. Стратегии, включающие приобретение опционов «с выигрышем», используют выгоды высокой чувствительности к цене базисного товара, а позиция по опциону в этом случае сближается с позицией по базисному товару.
Как было сказано выше, дельта используется для создания «мгновенной» позиции хеджа. Теоретически эту позицию необходимо постоянно корректировать из-за изменения дельты вследствие изменения цены базисного инструмента. Это известно как дельта-нейтральный хедж. При изменениях цены базисного инструмента хедж посредством опциона должен быть скорректирован путем изменения цены базисного инструмента и дельты.
Предположим, например, что опцион имеет дельту 0,75, а хеджер владеет базисным инструментом на сумму 10 млн. долл.
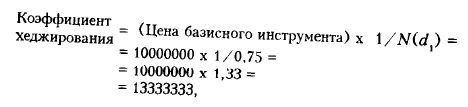
т.е. 1333333 единиц опциона на 10000000 единиц базисного инструмента.
|