Модель Блэка-Шоулза

Поскольку цена опциона является функцией цены акции, страйка, волатильности, времени до истечения срока и краткосрочных процентных ставок, то было бы естественно вывести формулу, по которой можно было бы вычислять цену опциона по этим переменным.

С тех пор как в 1973 г. стали торговать биржевыми опционами, было разработано много моделей. Большинство из них были нацелены на усовершенствование одной из первых введенных моделей – модели Блэка-Шоулза. Эта модель была создана в начале 1973 г. вскоре после начала торгов по биржевым опционам. Как только она была опубликована, у нее появилось множество приверженцев. Применение основной формулы этой модели не представляет затруднений – она проста, и количество переменных в ней мало.

Формула утверждает, что

Важным побочным результатом применения модели является точное значение дельты опциона, т. е. ожидаемой относительной величины изменения цены опциона при малом изменении цены акции. Дельта опциона появилась в гл. 2, ее еще называют коэффициентом хеджирования. Имеет место

Дельта = N(d₁)

Эта формула столь проста, что ее легко можно приспособить к большинству известных программируемых калькуляторов. Некоторые из таких калькуляторов можно увидеть даже в торговом зале, где их используют биржевики, следящие за динамикой текущей стоимости опционных премий. Компьютеры могут производить расчеты с большой скоростью, и потому большое количество вычислений по модели Блэка-Шоулза может быть осуществлено за очень короткий промежуток времени.

Таблицы нормальной кумулятивной функции распределения можно найти в большинстве книг по статистике. Однако для вычислительных целей было бы очень нецелесообразно постоянно отыскивать нужные значения по таблицам. Поскольку кривая нормальной плотности является гладкой (она имеет «колоколообразную» форму и часто используется для описания распределения популяции), то кумулятивная функция распределения для любого вещественного аргумента s может быть аппроксимирована формулой:

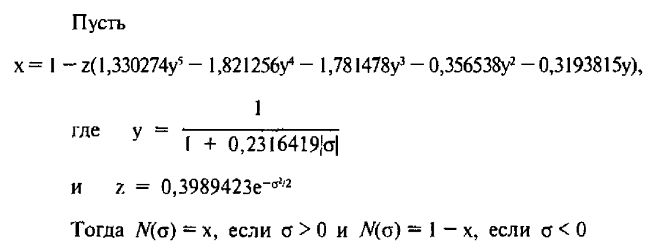
Эта аппроксимация весьма точная и вполне подходит для определения цены опционов, так как инвесторы, конечно, не интересуются тысячными долями пункта, когда дело касается цен опционов.

Пример. Предположим, что акции XYZ стоят 45 пунктов. Рассматривается колл «июль, 50», до истечения срока которого остается 60 дней. Наша цель – определить стоимость этого колла. Предположим еще, что волатильность акции XYZ равна 30%, а безрисковая процентная ставка на данный момент – 10%. Вычисление теоретической стоимости проведем подробно, чтобы читатели, желающие самостоятельно запрограммировать модель, имели бы основу для сравнения своих расчетов.

Сначала в соответствии с формулами, приведенными выше, определим параметры t, d₁ и d₂

Слишком много вычислений связано с получением значений полинома пятой степени, чтобы приводить их здесь. Окончательным результатом будет значение

х = 0,74865.

Поскольку мы определяем значение нормальной кумулятивной функции распределения для отрицательного аргумента, то это значение получается вычитанием х из 1.?

N(d₁) = М-0,67025) = 1 – х = 0,74865 = 0,25134

Аналогично

N(d₂) = М-0,79179) = 1 – 0,78579 = 0,21421

Теперь, возвращаясь к приведенной выше формуле, мы можем завершить вычисление теоретической стоимости колла «июль, 50».

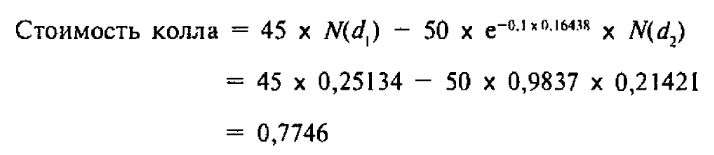
Таким образом, теоретическая стоимость колла «июль, 50» слегка превышает ¾ пункта. Отметим, что попутно мы вычислили дельту колла как величину N(d₁) и она оказалась чуть больше 0,25. Это значит, что при малом изменении цены акции цена колла «июль, 50» изменится почти на ¼ от величины этого изменения.

Как можно надеяться, этот пример отвечает на многие вопросы, поставленные читателями первого издания книги. Читателю, заинтересованному в более глубоком изложении модели, включая и конкретный вывод формулы ценообразования опционов, следует обратиться к статье «Факты и иллюзии при использовании опционов». Одним из менее очевидных выводов модели является то, что при увеличении безрисковой процентной ставки цена опциона возрастает. Можно также заметить, что модель правильно отражает влияние волатильности, цены акции и времени до истечения срока на стоимость опциона – с их увеличением цена опциона также возрастает.

Характеристики модели

Некоторые аспекты этой модели стоит рассмотреть подробнее. Во-первых, читатель, возможно, обратил внимание на то, что модель не учитывает дивидендов, выплачиваемых по обыкновенным акциям. Как было ранее показано, дивиденды оказывают отрицательное влияние на цену колла. Поэтому непосредственное использование этой модели ведет к завышению цены колла, особенно в случае с акциями, по которым выплачиваются относительно большие дивиденды. Имеются способы, позволяющие справиться с этой проблемой. Фишер Блэк, один из соавторов модели, предложил следующий способ. Нужно скорректировать текущую цену акции, используемую в модели, вычитая из нее текущую стоимость дивидендов, которые должны будут выплачены до истечения срока. А затем уже следует вычислить стоимость опциона. Во- вторых, предположим, что истечение срока опциона наступает непосредственно перед последней датой выплаты дивиденда, предшествующей фактическому истечению срока опциона. И снова нужно скорректировать цену акции и вычислить стоимость опциона. А далее выбрать из двух теоретических цен опционов наибольшую. Другой, менее точный, способ состоит в использовании весовых множителей для цен опционов. Весовые коэффициенты должны быть основаны на дивидендных выплатах, и больший вес приписывается колл-опционам с высокодоходными акциями. Следует обратить внимание на то, что во многих приложениях, которые будут рассмотрены, нет необходимости знать точную теоретическую цену колла. Поэтому коррекцию с учетом дивидендов можно для некоторых стратегий не применять.

Модель основана на предположении о логнормальном распределении вероятностей для цены акции. Хотя исходным распределением служит нормальное, по использование экспоненты приводит к логнормальному распределению. Для менее знакомых со статистикой читателей отметим, что нормальное распределение имеет колоколообразного вида кривую плотности вероятности. Это – наиболее известное вероятностное распределение. Проблема, возникающая при использовании нормального распределения, состоит в том, что оно допускает и отрицательные значения цены акции, чего в реальности не бывает. Поэтому, как правило, используется именно логнормальное распределение, так как в этом случае цена акции может принимать значения лишь между нулем и бесконечностью. Кроме того, смещение цены вверх (смещение «быка»), свойственное логнормальному распределению, представляется логически оправданным, так как цена акции может упасть максимум на 100%, а возрасти более чем на 100%. Многие модели ценообразования опционов, которые появились раньше модели Блэка-Шоулза, пытались использовать эмпирические распределения. Эмпирическое распределение имеет отличную от нормального и логнормального распределения форму кривой плотности. Однако разумные эмпирические распределения для цены акции не сильно отличаются от логнормального распределения, хотя в соответствии с ними часто предполагается, что цена акции имеет более высокую вероятность оставаться стабильной, чем для логнормального распределения. Критики модели Блэка-Шоулза утверждают, что эта модель, в основном из-за того, что она использует логнормальное распределение, как правило, переоценивает коллы «в деньгах» и недооценивает коллы «без денег». В некоторых случаях эта критика справедлива, по это вовсе не умаляет достоинств модели, проявляющихся во многих ее приложениях. Конечно, если инвестор собирается купить или продать коллы исключительно на основании их вычисленной стоимости, это создаст большую проблему. Однако если стратегические решения должны приниматься на основании других факторов, перевешивающих значимость правильной оценки стоимости колла, небольшие отличия в цене не будут иметь значения.

Вычисление волатильности всегда представляет собой сложную проблему. В модели Блэка-Шоулза волатильность определяется как стандартное отклонение цены акции в годовом исчислении. Эмпирическое ее значение задается обычной статистической формулой:

Если волатильность рассчитывается па основании прошлых цен акции, ее называют исторической волатильностью. Волатильность акции, как правило, изменяется во времени. Некоторые предсказуемые факторы, такие как сплит акций, приводящие к увеличению числа акций, могут уменьшить волатильность. Другие не столь хорошо определяемые факторы могут также изменить волатильность. Поскольку волатильность является ключевым элементом модели ценообразования, для применения модели важно использовать разумную оценку текущей волатильности. Понятно, что стандартное отклонение в годовом исчислении не является точной оценкой, так как год – слишком большой период времени. Последние работы многих исследователей подсказали идею о том, что, возможно, для получения оценки текущей волатильности имеет смысл последним ценам акции приписывать более высокий вес, чем старым ценам. Этот подход вполне возможен, однако на пути его применения может возникать также много ошибок. И проблема точного вычисления волатильности остается. Она очень важна, так как модель весьма чувствительна к изменению волатильности.

Вычисление логнормальной исторической волатильности. Приведенные выше расчеты не дают удовлетворительного значения параметра волатильности для модели Блэка-Шоулза, так как в модели предполагается, что нормально распределен именно логарифм изменения цены, а не сама цена. Поэтому величины P_i в приведенной выше формуле следует изменить.

Пример. Сегодняшняя цена закрытия акции XYZ равна 51 пунктам, а вчерашняя – 50. Процентное изменение цены за день составило 51/50 = 1,02. Натуральный логарифм от 1,02 равен

ln(51/50) = ln(1,02) = 0,0198

Можно сказать, что в арифметическом смысле цена акции возросла на 2%, по в логарифмическом смысле – только на 1,98%.

Если цена акции падает, то расчеты приведут к отрицательным числам. Предположим, что на следующий день цена акции упадает с 51 до 50 пунктов. Число, которое должно было бы далее использоваться в формуле для волатильности, равно

ln(50/51) = ln(0,9804) = 0,0198?

Теперь можно заново переписать формулу для волатильности, использую концепцию логнормальности. Она будет давать волатильность, согласованную с моделью Блэка-Шоулза.

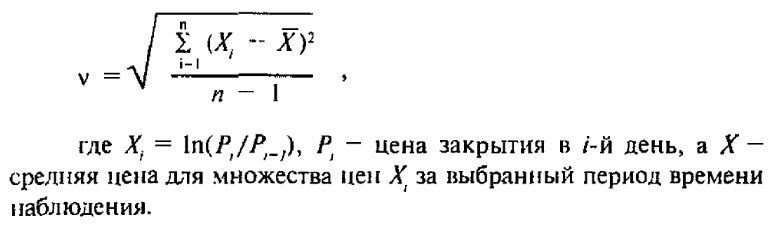
Для определения 10-дневной исторической волатильности потребуется 11 наблюдений. В следующем примере читатель может не обращать внимания на некоторые детали, если он не собирается вычислять волатильность самостоятельно. Эти детали приводятся для математиков и программистов, желающих проверить себя. (AVG означает среднее.)

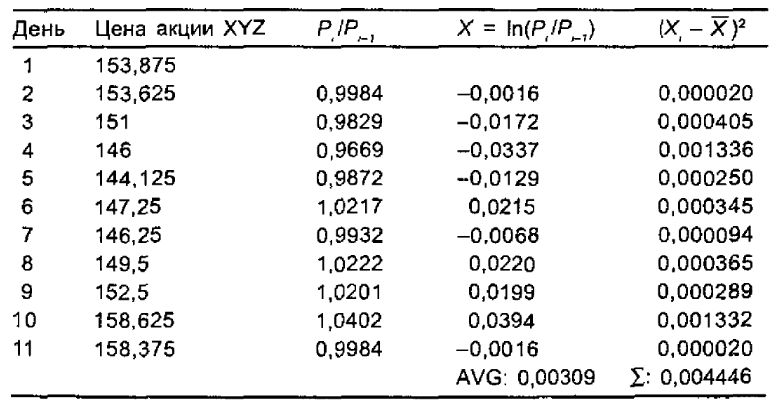
Среднее всех логарифмов (4-й столбец) за 10 дней составляет 0,00309.

Отклонение каждою логарифма от среднего возводится в квадрат, и затем результаты суммируются (5-й столбец). Например, член, отвечающий 1-му дню, дает (-0,0016 – 0,00309)² = 0,00002. Это – наибольшая величина в крайне правом столбце.

Такой расчет проводится для каждого числа в столбце логарифмов. Сумма всех слагаемых равна 0,004446. Теперь

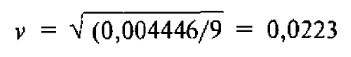
Это – 10-дневная волатильность. Чтобы выразить ее в годовом исчислении, ее нужно помножить на корень квадратный из числа торговых дней в году. Поскольку в году приблизительно 260 торговых дней, окончательное значение волатильности получается по формуле:

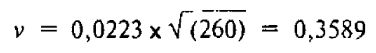
Таким образом, можно сказать, что волатильность акции XYZ в годовом исчислении равна 36%.

Это – корректный способ вычисления исторической волатильности. Очевидно, что инвестор, если того пожелает, может вычислять 10-, 20-, 50-дневную и годовую волатильности, равно как и волатильность для любого другого количества дней. В определенных случаях инвестор, изучая и сопоставляя различные волатильности между собой, может извлечь ценную информацию об акциях и опционах на них.

На практике случается так, что инвестор может предоставить возможность самому рынку вычислить для него волатильность. В этом случае говорят о наведенной волатильности (implied volatility), т. е. волатильности, которая наводится самим рынком. В этом понятии заложено предположение, что для опционов со страйком, близким к текущей цене акции, и относительно большими объемами торговли рынок справедливо оценен. Это в некотором роде аналог гипотезы эффективного рынка. И действительно, если на рынке проявляется большой интерес к близким ничейным опционам, то они, как правило, оцениваются справедливо. При сделанном предположении следует вывод: если фактическая цена опциона является справедливой, то ее в рамках модели Блэка-Шоулза можно зафиксировать, а волатильность интерпретировать как неизвестный параметр. Волатильность в таком случае может быть определена итеративным методом. Эта итеративная процедура вычисления волатильности может быть реализована для каждого опциона на конкретные базовые акции. В этом случае в результате могут возникнуть несколько разных значений волатильности для одной и той же акции. Однако если взвесить эти результаты по торговым объемам и по величинам выигрыша и проигрыша опционов, то можно получить единственное значение волатильности для базовой акции. Эта волатильность определяется ценами закрытия всех опционов на базовую акцию в рассматриваемый день.

Пример. Акции XYZ стоят 33 пункта, а цены закрытия представлены в табл. 30-1. Каждый опцион имеет свою наведенную волатильность, отличную от остальных и полученную в результате вычисления волатильности из модели Блэка-Шоулза, приводящей к заданной цене закрытия для рассматриваемого опциона. Так, если использовать в качестве значения волатильности число 0,34, модель даст цену колла «январь, 30», равную 4½ пункта. Для получения волатильности самой акции необходимо сначала выбрать весовые коэффициенты, с помощью которых разные значения волатильности можно было бы разумным образом скомбинировать.

Весовые коэффициенты, отвечающие объемам торговли, легко рассчитываются. Коэффициентом для каждого опциона служит просто дневной объем, деленный на общий объем всех опционов на акции XYZ (табл. 30-2). Весовые коэффициенты, отвечающие отклонению текущей цены акции от страйка, могут не быть линейной функцией цены акции. Например, если один опцион «в деньгах» в 2 пункта, а другой – 4 пункта, то первому из них вовсе не обязательно следует приписывать вес, в два раза превышающий вес второго. Если опцион значительно «в деньгах» или значительно «без денег», то ему вообще не следует приписывать никакого веса вне зависимости от объема торговли. Любая функция параболического вида может оказаться достаточной:

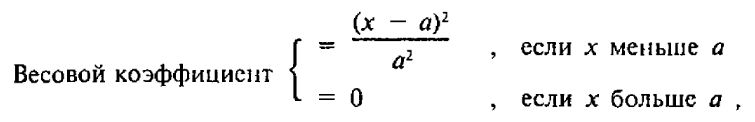
где переменная x – относительное расстояние между ценой акции и страйком, а параметр а – максимальное относительное расстояние, для которого разработчик моделей еще будет определять наведенную волатильность.

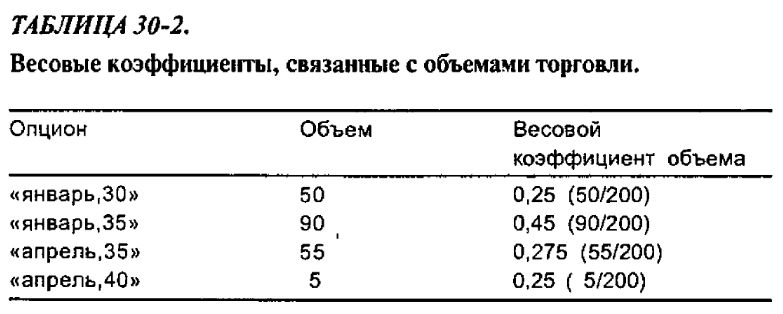
Пример. Инвестор приходит к выводу, что он не будет приписывать весовые коэффициенты опционам, чьи страйки более чем на 25% отличаются от текущей цены акции. Параметр а в таком случае можно положить равным 0,25. В табл. 30-3 демонстрируется, как могут быть рассчитаны весовые коэффициенты для цены акции XYZ в 33 пункта. Для одновременного учета двух типов взвешивания каждая пара весовых коэффициентов, отвечающая рассматриваемому опциону, перемножается между собой, и результат умножается на наведенную волатильность этого опциона. Эти произведения суммируются по всем рассматриваемым опционам, а затем полученная сумма делится на сумму парных произведений одних лишь весовых коэффициентов. Формально это может быть записано следующим образом:

В нашем примере вычисления дают наведенную волатильность акции XYZ в 29,8% (табл. 30-4). Отметим, что наведенная волатильность, равная 0,298, не равна ни одному из отдельных значений наведенных волатильностей опциона. Ее можно рассматривать как некоторый сводный показатель, придающий больший вес торгуемым в больших объемах и почти опционам «при деньгах» и значительно меньший вес плохо торгуемому (5 контрактов) коллу «апрель, 40» значительно «без денег». Эта наведенная волатильность, тем не менее, является стандартным отклонением и потому может использоваться везде, где требуется обычная волатильность.

Этот способ вычисления наведенной волатильности довольно точен и, как оказывается, демонстрирует чувствительность к изменению волатильности акции. Например, когда рынок становится рынком «быков» или «медведей» (демонстрируя сильные взлеты или падения), большинство акций также показывают свою неустойчивость. Опционные премии довольно быстро возрастают, и этот способ вычисления наведенной вероятности способен быстро уловить изменения. Однако для получения окончательного значения волатильности акции кое-что нуждается в тонкой настройке. Если рассматривать динамику наведенной волатильности акции по дням, особенно для опционов, торгуемых недостаточно активно, то оказывается, что она изменяется значительно сильнее, чем это хотелось бы. Эффект сглаживания может быть достигнут, если использовать скользящее среднее значений наведенной волатильности за последние 20 или 30 дней. В качестве альтернативы можно было бы использовать быстрое вычисление наведенной волатильности, не требующее запоминания большого количества данных за предшествующие дни. Например, окончательную волатильность на сегодняшний день можно было бы получить, добавляя 5% сегодняшней наведенной волатильности к 95% вчерашней окончательной волатильности. Этот способ требует запоминания из всей предыстории рынка только одного – вчерашней окончательной волатильности. Такой способ также обладает свойством сглаживания.

Как только наведенная волатильность вычислена, ее можно использовать в модели Блэка-Шоулза (или в любой другой модели) в качестве параметра волатильности. В соответствии с моделью Блэка-Шоулза, требующей знания наведенной волатильности акции, можно вычислять теоретическую стоимость каждого опциона.

Поскольку наведенная волатильность акции будет, скорее всего, отличаться от наведенной волатильности конкретного опциона, то между фактической ценой закрытия опциона и теоретической ценой, вычисленной по модели, будет расхождение. Эта разность цен будет говорить о том, что рассматриваемый опцион теоретически переоценен или недооценен по сравнению с другими опционами на ту же самую акцию.