Гамма

Упрощенно говоря, гамма означает, как быстро меняется дельта по отношению к изменению цены базовой акции. Известно, что дельта колла возрастает по мере того, как колл из опциона «без денег» превращается в опцион «в деньгах». Гамма в этом смысле является точной характеристикой того, насколько быстро возрастает дельта.

Пример. Предположим, что при цене акции XYZ в 49 пунктов колл «январь, 50» имеет дельту 0,50, а гамму 0,05. Если цена акции возрастет на 1 пункт и станет равной 50, то дельта колла возрастет па величину гаммы, т. е. увеличится с 0,50 до 0,55.

Как и в случае с дельтой, гамма может быть выражена в процентах. Как эта используется при вычислении увеличения или уменьшения дельты, покажем на примере.

Пример. Снова предположим, что при цене акции XYZ в 49 пунктов колл «январь, 50» имеет дельту 0,50, а гамму 0,05. Если цена акции возрастет па 2 пункта до 51, то дельта колла возрастет на 5% от изменения цены акции, так как гамма равна 0,05, или 5%. Пять процентов от изменения цены составит 0,05 х 2 = 0,10. Таким образом, дельта повысится на 0,10 – с 0,50 до 0,60.

Очевидно, что дельта не может при каждом увеличении цены акции на 1 пункт возрастать на 0,05, так как в таком случае она довольно быстро превысит 1,00, а известно, что максимальное значение дельты равно 1,00. Поэтому очевидно, что сама гамма меняется. Вообще говоря, гамма принимает максимальное значение, когда цена акции находится вблизи страйка опциона. По мере продвижения цены акции от страйка в любом направлении гамма убывает, приближаясь к своему минимальному значению – нулю.

В содержательном смысле это означает, что опционы значительно «в деньгах» или значительно «без денег» имеют гамму, близкую к нулю. Это соответствует тому, что дельта соответствующих опционов очень слабо меняется при изменении цены акции на 1 пункт, что вполне естественно.

Пример. Предположим, что акции XYZ стоят 25 пунктов, а колл «январь, 50» имеет дельту, практически равную нулю. Если цена акции повысится на 1 пункт до 26, то колл все еще останется глубоко «без денег», а его дельта все также будет близка к нулю. Поэтому гамма этого колла практически равна нулю, так как дельта при изменении цены акции на 1 пункт практически не изменилась.

Аналогичным образом пут «январь, 45» на акции XYZ при цене акции 45 будет иметь дельту, равную –1,0. Если цена акции повысится на 1 пункт до 26, то дельта пута не изменится, так как он все еще остается значительно «в деньгах», и его дельта должна потому равняться –1,0. Таким образом, гамма подобного опциона также равна нулю, так как дельта остается практически неизменной при возрастании цены базовой акции на 1 пункт.

Отметим, что гамма любого опциона выражается положительным числом – как для пута, так и для колла.

Полезно было бы знать также и другие свойства гаммы. При приближении латы истечения срока гамма опциона «при деньгах» значительно возрастает. Рассмотрим опцион, до истечения срока которого остается один или два дня. Если он только «при деньгах», то его дельта приблизительно равна 0,50. Однако если цена акции повысится на 2 пункта, то дельта опциона подскочит почти до 1,00, так как до истечения срока остается очень мало времени. Поэтому гамма приближенно будет равна 0,25 (дельта возросла на 0,50 при изменении цены акции на 2 пункта), что значительно больше тех малых величин гаммы, которые свойственны опционам с несколькими неделями или месяцами до истечения срока. Такое же повышение цены базовой акции на 2 пункта определенно не даст столь значительного повышения дельты для более долгосрочных опционов.

Опционы «без денег» демонстрируют иное соотношение между гаммой и временем до истечения срока. Опцион «без денег», срок которого вскоре должен истечь, имеет очень небольшую дельту и потому малую гамму. Однако если до истечения срока данного опциона остается еще достаточно много времени, то гамма этого опциона будет больше, чем у опциона с небольшим временем до истечения срока.

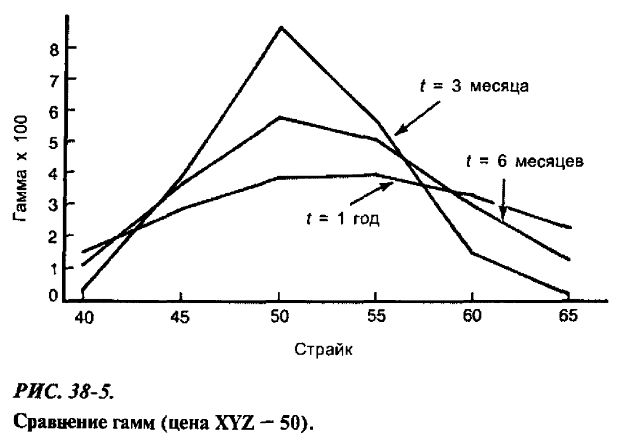
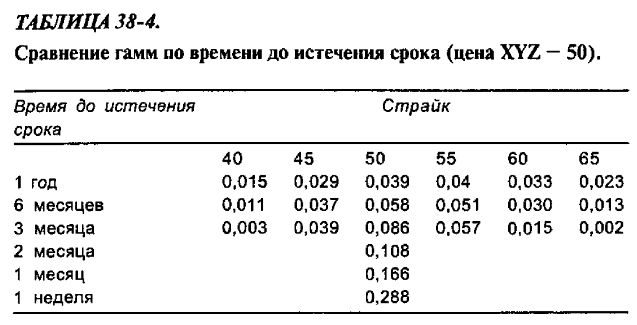
На рис. 38-5 и в табл. 38-4 изображены графики гаммы для трех опционов с разными временами до истечения срока в зависимости от страйка. Эти графики хорошо иллюстрируют взаимоотношение гаммы и времени до истечения срока. Обратим внимание на то, что краткосрочные опционы имеют очень низкие значения гаммы в случае, когда эти опционы значительно «в деньгах» или значительно «без денег», и наибольшие значения гаммы в случае опционов «при деньгах» (при 50). Напротив, самый долгосрочный, 1-летний, опцион имеет наибольшие значения гаммы из всех трех опционов в случае, когда этот опцион значительно «в деньгах» или «без денег». Соответствующие числовые данные приведены в табл. 38-4. В ней содержится и некоторая дополнительная информация, а именно значения гаммы для еще более коротких периодов времени до истечения срока. Обратите внимание, как резко возрастает гамма при приближении истечения срока для опциона «при деньгах». Когда остается одна неделя, то гамма уже больше 0,28, а это означает, что дельта такого колла возрастет сразу с 0,50 до 0,78 при изменении цены акции всего с 50 до 51.

Гамма зависит также и от волатильности базового инструмента. Опционы «при деньгах» на менее волатильную акцию будут иметь более высокие значения гаммы, чем аналогичные опционы на более волатильную акцию. Следующий пример демонстрирует это свойство.

Пример. Предположим, что как акции XYZ, так и акции ABC стоят 49 пунктов. Кроме того, акции XYZ являются более волатильными (прогнозируемая волатильность равна 30%) по сравнению акциями АВС (20%). В этом случае схожие опционы на эти два типа акций будут иметь существенно отличающиеся значения гаммы.

Отметим, что опционы «при деньгах» («январь, 50» и «февраль, 50») на АВС, т. е. менее волатильную акцию, имеют более высокие значения гаммы, чем соответствующие опционы на XYZ. Однако если обратиться к опционам с более высоким страйком («январь, 55»), то можно увидеть, что опционам на более волатильные акции соответствуют несколько большие значения гаммы. Для опционов с еще большим значением страйка («январь, 60» и «февраль, 60») более волатильные акции по сравнению с неволатильными дают также большее значение гаммы, но различие при этом становится значительным.

Рассмотренные понятия имеют значение для трейдера, если он задумывается о взаимоотношении волатильности и дельты. Трейдер обнаруживает, что для неволатильных акций дельта опциона даже незначительно «в деньгах» значительно возрастает. Это происходит оттого, что поскольку акции неволатильные, покупатели не готовы платить за опцион большую временную премию. В результате гамма также оказывается большой, поскольку по мере того, как опцион становится «в деньгах», увеличение дельты будет более значительным, чем в случае неволатильных акций. С опционами «без денег» совсем другая история. Поскольку неволатильным акциям трудно достичь некоторого страйка, приводящего опцион в состояние «без денег», то дельта опциона «без денег» мала, и она не будет изменяться быстро (т. е. также и гамма мала).

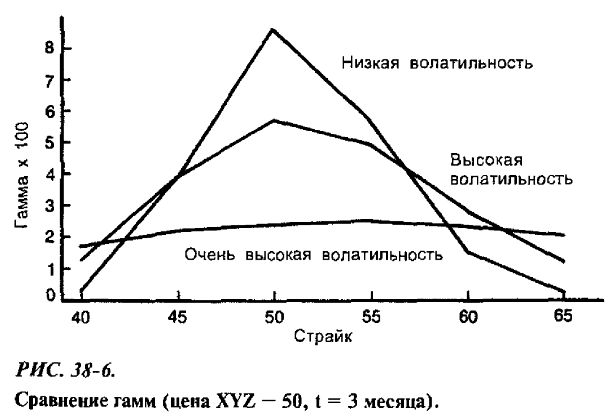
Эти соображения представлены на рис. 39-6 и в табл. 39-5. На рисунке изображены графики гаммы для схожих опционов, но на акции с разными волатильностями. На графиках представлен случай, когда цена XYZ равна 50, а до истечения срока остается 3 месяца.

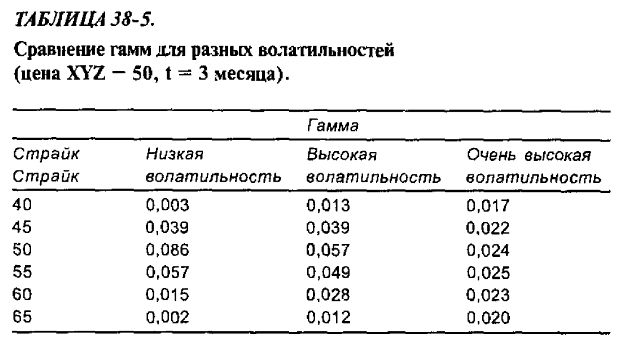
Отметим, что для очень волатильной акции гамма при 3 месяцах до истечения срока почти не меняется по страйкам. Это значит, что дельта всех опционов на столь волатильную акцию будут значительно изменяться даже при изменении цены базовой акции на 1 пункт. На это обстоятельство следует обратить внимание нейтральному трейдеру, поскольку позиция, которая вначале является дельта-нейтральной, может быстро измениться, если базовая акция очень волатильная. Как следует из этой таблицы, дельты опционов в таком «нейтральном» спрэде могут быстро измениться, превращая его в спрэд, весьма далекий от нейтрального. Эта тема будет развита позже в этой главе.

Напомним, что ранее мы использовали дельту опционов для конструирования эквивалентной позиции по акциям для всей опционной позиции или всего портфеля опционов. Гамма опционов может применяться в аналогичном ключе. Соответствующий пример приводится ниже, при этом используются те же самые ценные бумаги из рассмотренного выше примера, посвященного дельте позиции. Важно отметить, что гамма самой базовой ценной бумаги равна нулю. Это так, поскольку дельта базовой ценной бумаги никогда не меняется (в этом случае дельта всегда равна 1,0). Но гамма характеризует скорость изменения дельты, и поскольку дельта не меняется, то гамма базовой ценной бумаги равна нулю.

Пример. При цене акции XYZ в 31¾ пункта существует следующая позиция. Напомним, что она похожа на длинный стрэддл (или бэкспрэд) в том, что при достаточно большом изменении цены акции в любую сторону к истечению срока по этой позиции возникает высокая потенциальная прибыль. В дополнение к перечню значений дельты приводятся и значения гаммы. Отметим, что, поскольку абсолютные значения гаммы являются малыми величинами, их вычисляют обычно с точностью до трех или четырех знаков после запятой.

Как и прежде, позиция является дельта-длинной по 700 акциям. Кроме того, теперь можно видеть, что она характеризуется положительной гаммой, соответствующей более 300 акциям. Это значит, что при изменении цены акций XYZ на 1 пункт можно ожидать изменения дельты на эквивалент в 328 акций. Иначе говоря, если это движение в 1 пункт акции произойдет, то дельта увеличится до +1014 (текущее значение дельты, 686, плюс значение гаммы, 328). Однако если цена акции понизится на 1 пункт, то дельта уменьшится и станет равной +358 (текущее значение дельты, 686, минус значение гаммы, 328).

Отметим, что в приведенном выше примере в случае, если акции XYZ продолжат свой рост, то гамма останется положительной (хотя со временем она и будет уменьшаться) и потому дельта будет продолжать возрастать. Это значит, что позиция становится все более дельта-длинной. Этот факт представляется естественным, если заметить, что в позиции существуют избыточные длинные коллы и при повышении цены акции их выигрыш становится все больше. Напротив, если цена акции будет последовательно снижаться, дельта будет уменьшаться и довольно быстро станет отрицательной величиной, а это будет означать, что позиция в целом стала дельта-короткой. Как мы видим, позиция действительно напоминает длинный стрэддл – она становится дельта-длинной при подъеме рынка и дельта-короткой – при его падении.

Длинные опционы, как путы, так и коллы, имеют положительную гамму, в то время как короткие опционы – отрицательную. Поэтому если гамма позиции трейдера положительна, то это значит, что он имеет чистую длинную опционную позицию и, как правило, надеется на большое движение рынка. И, наоборот, если гамма позиции трейдера отрицательна, то это значит, что он имеет чистую короткую опционную позицию и желает, чтобы рынок оставался относительно стабильным.

Отметим, что позиция может быть дельта-нейтральной, но при этом иметь значительную гамму (например, если трейдер владеет путами и коллами с противоположными дельтами, то его позиция дельта-нейтральна, но с положительной гаммой, так как все опционы – длинные). Если позиция трейдера дельта-нейтральна, то это значит, что в данный момент рыночный риск по его позиции отсутствует, но гамма позиции показывает ему, какой риск может возникнуть, если на рынке произойдут изменения. Об этом мы поговорим более подробно в этой главе позже.