|
Обсуждение этого фактора было ранее отложено, так как он труднее для понимания. Ему мы решили также уделить некоторое внимание, так как встречаются трейдеры, которые иногда прибегают к его использованию. Читатели, не заинтересованные в более близком знакомстве с этим фактором, могут пропустить этот раздел.
Напомним, что речь идет о шестом факторе риска для произвольной опционной позиции. Гамма гаммы является величиной, характеризующей изменение гаммы при изменении цены акции.


Напомним, что ранее при обсуждении гаммы говорилось о том, что гамма меняется. Следующий пример основывается на примере, уже использовавшемся ранее.
Пример. Предположим, что акции XYZ стоят 49, а КОЛЛ «январь, 50» имеет дельту 0,50 и гамму 0,05. Если цена акции возрастет на 1 пункт до 50, то дельта колла увеличится на величину гаммы, т. е. с 0,50 до 0,55. Приближенно можно считать, что если цена акции возрастет еще на 1 пункт до 51, то дельта увеличится еще на 0,05 до величины в 0,60.
Очевидно, что дельта не может постоянно увеличиваться на 0,05 каждый раз, когда цена акции возрастает на 1 пункт, так как в таком случае она рано или поздно превысила бы 1,00. Поэтому становится понятным, что гамма должна меняться.
На самом деле гамма уменьшается по мере того, как цена акции удаляется от страйка. Так, при цене акции 51 гамма, возможно, будет равна лишь 0,04. Поэтому если цена акции повысится до 52, то дельта колла возрастет только на 0,04 и станет равной 0,64. Следовательно, гамма гаммы равна –0,01, так как гамма уменьшилась с 0,05 до 0,04, когда цена акции повысилась на 1 пункт.
По мере того как цена акции продолжает возрастать, гамма становится все меньше и меньше. В конце концов по достижении ценой акции уровня 60 дельта практически становится равной 1,00, а гамма – 0,00.
Это изменение гаммы при изменении цены акции и определяет гамма гаммы. Для нее используются и другие названия, но, поскольку ее применяет весьма ограниченный круг искушенных трейдеров, стандартного термина для нее до сих пор не существует. Как правило, трейдер применяет этот фактор риска ко всему своему портфелю с целью оценить, как быстро портфель реагирует на изменение позиционной гаммы.
Пример. Акции XYZ стоят 31¾ пункта, а факторы риска принимают следующие значения:
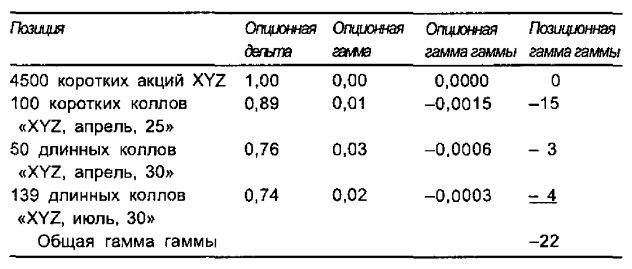
Напомним, что в том же примере, использовавшемся для интерпретации гаммы, позиция оказывалась дельта-длинной по 686 акциям и имела положительную гамму в 328 акций. Далее, теперь можно видеть, что сама гамма будет уменьшаться при возрастании цены акции (гамма гаммы отрицательна) и увеличиваться при падении цены акции. Как ожидается, при изменении цены акции на 1 пункт позиционная гамма будет увеличиваться или уменьшаться на величину в 22 акции.
Таким образом, при движении цены акции XYZ на 1 пункт вверх должно произойти следующее:
а) дельта увеличится с 686 до 1014 (на величину гаммы),
б) гамма уменьшится с 328 до 306, свидетельствуя о том, что дальнейшее движение вверх на 1 пункт цены акции приведет к увеличению дельты меньшего размера.
Можно построить общую картину того, как гамма гаммы изменяется в различных случаях – для опционов «в деньгах» и «без денег», для разных периодов до истечения срока. В следующей таблице для двух индексных коллов – «январь, 350» с одним месяцем до истечения срока и «декабрь, 350» с 11 месяцами до истечения срока – приводятся дельта, гамма и гамма гаммы при различных ценах индекса.
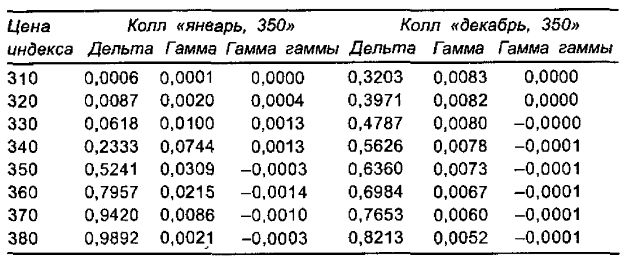
На основании таблицы можно сделать определенные выводы, не все из которых на первый взгляд очевидны. Прежде всего, гамма гаммы для долгосрочных опционов очень мала. Этого следовало ожидать, так как дельта долгосрочного опциона меняется очень слабо. Следующий вывод сделать легче, если обратиться к табличным данным для краткосрочного колла «январь, 350». Гамма гаммы практически равна нулю для опционов значительно «без денег». Однако по мере возрастания индекса гамма гаммы принимает все большие положительные значения и достигает максимума, хотя опцион все еще «без денег». Когда цена индекса совпадает со страйком, гамма гаммы уже оказывается отрицательной. Далее она остается отрицательной и достигает своего наибольшего отрицательного значения при опционе с незначительной прибылью «в деньгах». С этого момента она, оставаясь отрицательной, все ближе и ближе подходит к нулю, достигая его при опционах значительно «в деньгах».
Можно ли разобраться в свойствах этого фактора риска до конца, не проделывая сложных математических расчетов? Думается, что можно. Отметим, что дельта начинает с очень небольших значений, когда опцион имеет глубоко «без денег». Затем она возрастает – сначала медленно, затем все быстрее, пока не окажется чуть ниже 0,60 для опциона «при деньгах». С этого момента она продолжит свой рост, но значительно медленнее, когда опцион становится «в деньгах». Эту динамику дельты можно проследить и с помощью гаммы. Гамма – это изменение дельты, поэтому она начинает медленно возрастать, далее этот рост усиливается по мере приближения индекса к страйку, а затем начинает уменьшаться, когда опцион становится «в деньгах», всегда оставаясь положительной, поскольку дельта может изменяться при росте цены индекса только в положительном направлении. Наконец, гамма гаммы определяет изменения гаммы, поэтому она также сначала является положительным числом, и, пока гамма растет, она остается положительной, но, когда гамма начинает убывать, гамма гаммы начинает принимать отрицательные значения.
В целом, гамму гаммы используют лишь опытные трейдеры, притом в отношении крупных опционных позиций, для которых не очевидно, что будет происходить с гаммой при изменении цены акции. Трейдеры часто имеют представление о дельте своей позиции. Более того, они даже чувствуют, как будет меняться дельта при движении цепы акции (т. е. они осознают, какова гамма). Но также опытные трейдеры хорошо знают и то, что даже позиции с пулевыми значениями и дельты, и гаммы на момент их организации могут со временем стать дельта-длинными или дельта- короткими. Именно гамма гаммы может помочь трейдеру узнать, как скоро и в какой степени это произойдет.
|