|
Каждая комбинация в любой момент времени имеет свою специфичную платежную функцию. Это означает, что для любых базовых активов и любых опционных стратегий есть универсальная характеристика. С формальной точки зрения ее можно записать в виде PF(B, S, х, t, par), где В – конкретный базовый актив, S – конкретная опционная стратегия, х – возможная цена базового актива, t – момент времени, для которого вычисляется платежная функция par – значения других параметров рынка.


Частным случаем функционала PF(B, S, x, t, par) является платежная функция комбинации PF(B, S, х) на фиксированный момент времени. Для стратегий, в которых участвуют опционы только одной серии, этим моментом может быть, например, дата экспирации. Для календарных спредов этим моментом может быть первая дата экспирации. Вообще говоря, для формирования функции PF(B, S, х) мы фиксируем ту дату, на которую хотим рассчитать показатели комбинации. Представление опционной стратегии в каждый момент времени в виде платежной функции имеет важнейшее значение для принятия решений. Зная платежную функцию и значения ее аргументов в интересующий нас момент будущего, мы можем прогнозировать доход или убыток стратегии. При этом у нас появляется возможность сравнивать между собой разные опционные стратегии для разных базовых инструментов.
Универсальными критериями мы называем функционалы, которые сопоставляют паре {базовый актив х опционная стратегия} действительное число позволяющее сравнивать между собой любые возможные пары. Например, бабочку из коллов для QQQQ и медвежий пут-спред для IBM. Аналогично универсальности платежной функции, как характеристики опционной комбинации мы строим универсальные критерии для того, чтобы иметь возможность сравнивать и упорядочивать по предпочтительности разные опционные стратегии для разных базовых активов.
Рассмотрим следующую ситуацию: допустим, мы оцениваем только стратегии с одновременным истечением всех входящих в них опционов. И пусть нас интересует оценка стоимости комбинаций только в момент экспирации. Мы не можем знать будущую цену базового актива, но можем определить вероятностное распределение будущих цен. Формально этот прогноз представляется для каждого базового актива функцией плотности вероятности, аргументом которой является будущая цена базового актива, а значение функции – это вероятность реализации такой цены в интересующий нас момент будущего Предположим, что мы каким-либо образом получили функции плотности вероятности для цен базовых активов на момент экспирации. Обозначим их f(B, x) где В – базовый актив, х – его цена в момент экспирации опционов. Вычислим интеграл:
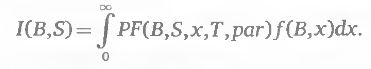
Здесь Т – момент экспирации. На языке теории вероятностей интегралы I(B, S) – это математические ожидания прибыли комбинации в момент экспирации. Они представляют собой типичные примеры универсальных критериев. Некоторые из таких критериев будут подробно описаны далее.
Для критериев такого типа совершенно естественно возникает суждение типа: если математическое ожидание прибыли от комбинации «бабочка из кол-лов для QQQQ» больше, чем математическое ожидание прибыли от комбинации «медвежий пут-спред для IBM», то первая комбинация лучше второй.
Обратим внимание на аргументы критериев I(B, S) – базовый актив и стратегию. Если мы вычислим такой критерий для каждой комбинации, входящей в нашу матрицу, то получим универсальный аппарат для сравнения всех элементов матрицы независимо от опционных стратегий, базовых активов и алгоритмов построения комбинаций.
Как было сказано выше, количество сравниваемых комбинаций может исчисляться миллионами. Это многообразие дает богатейший материал для поиска перспективных торговых вариантов, а универсальные критерии представляют собой необходимый инструментарий этого поиска.
Прогнозные универсальные критерии
Большинство универсальных критериев представляют собой численно выраженные прогнозы различных показателей. Поскольку будущая прибыль – это основное, что интересует инвестора, многие универсальные критерии являются прогнозом прибыльности комбинации на определенный момент времени в будущем. Большое значение имеет оценка относительной величины прибыли, т. е. частного от деления абсолютной прибыли на необходимую для вхождения в позицию сумму инвестиций. Не менее важен прогноз различных вариантов доходности – величины прибыли, нормированной с учетом времени нахождения в позиции.
Принципиальное значение для создания прогнозных универсальных критериев имеет прогноз будущей цены базового актива. Точность и представление прогноза могут быть совершенно различными. В литературе предлагается рассматривать варианты значений цены и присваивать им определенные вероятности наступления (Макмиллан, 2002). Это частный случай используемого нами прогноза в виде вероятностного распределения будущей цены. Такая функция использовалась в приведенной выше формуле 1.6.1 для расчета математического ожидания прибыли комбинации в момент экспирации. Применение различных функций плотности вероятности и аппарата теории вероятности порождает большой класс прогнозных универсальных критериев. Как будет показано ниже, грамотное построение и применение прогнозных универсальных критериев является чрезвычайно продуктивным с точки зрения выявления перспективных торговых возможностей.
Непрогнозные универсальные критерии
Для создания универсальных критериев могут также использоваться разнообразные количественные характеристики, не связанные напрямую с оценкой и прогнозом прибыльности или доходности. Например, инвестора могу] интересовать оценки риска, характеризующие потенциальные отклонения суммы его активов в период нахождения в позиции. В таких случаях критерии могут быть сконструированы на основе «греков». Целый ряд критериев может быть создан на основе характеристик изменчивости цен базового актива. Это достигается путем расчетов и комбинирования (разнообразными методами) исторической и подразумеваемой волатильностей. Другой возможностью является сочетание средних значений с показателями изменчивости. В результате возникают новые универсальные, но не прогнозные критерии.
|