|
Отличие от всех предыдущих подходов к оценке эффективности критериев, методика не базируется на регрессионном анализе. Сортируя комбинации по значениям критерия, мы предполагаем, что каждый последующий номер в упорядочении хуже предыдущих по вероятностным или другим характеристикам будущей прибыли. Тестирование этой гипотезы и лежит в основе данного показателя эффективности. Особенности расчетной методики позволяют применять ее только к критериям, прогнозирующим ожидаемую прибыль комбинаций. Ниже рассмотрена процедура вычисления данного показателя эффективности на примере стратегии «короткий стрэнгл/стрэдл».


Предположим, что мы открываем торговую позицию по п первым номерам в упорядочении, инвестируя в каждую комбинацию равную сумму (допустим, $ 100). Размер инвестиций будем считать равным маржевым требованиям. Поскольку мы условились нормировать значения критерия и прибыли на величину маржи, то при таком распределении капитала значение критерия в точности соответствует величине ожидаемой прибыли в долларовом эквиваленте. Открытие позиции по п первым комбинациям означает инвестицию в размере $ ЮОп. Прибыль такой позиции будет равна сумме прибылей составляющих ее комбинаций.
Проследим зависимость прибыли портфеля, состоящего из п первых в упорядочении комбинаций, от количества комбинаций, входящих в состав портфеля (т. е. от п, принимающего значения от 1 до 500). Если критерий действительно позволяет выявить лучшие комбинации, то на первых местах в упорядочении окажутся в основном прибыльные комбинации, а на последних – убыточные. В таком случае искомая зависимость будет представлять собой восходящую, изгибающуюся, выпуклую линию, достигающую максимума в точке, соответствующей порядковому номеру комбинации с нулевой прибылью. По прохождении этой точки линия становится нисходящей вплоть до достижения минимального значения.
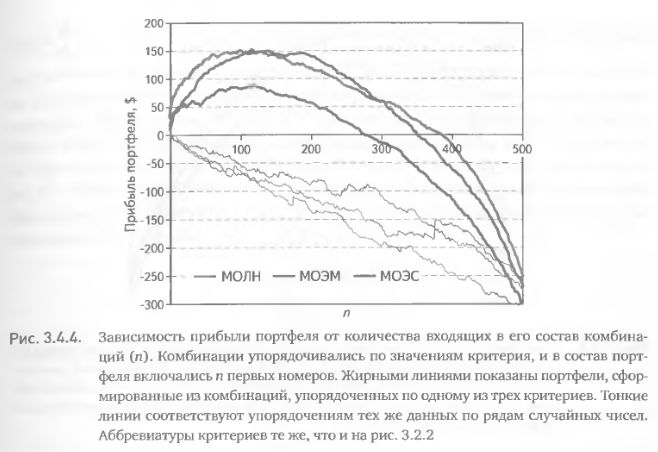
Жирные линии на рис. 3.4.4 иллюстрируют такие зависимости для трех критериев (МОЛН, МОЭМ и МОЭС), выражающих математические ожидания прибыли на основе различных распределений. Форма линий в общих чертах соответствует приведенному выше описанию, наводя на мысль о способности критериев ранжировать комбинации по их потенциальной прибыльности. Дополнительным подтверждением этого предварительного вывода может служить форма тонких линий на рис. 3.4.4. Эти линии были получены тем же путем, но при упорядочении комбинаций не по критериям, а по рядам случайных чисел. Легко заметить, что в случае упорядочения по критериям прибыли портфелей вначале растут (поскольку на первых местах в упорядочениях находятся преимущественно прибыльные комбинации), а затем начинают снижаться. С другой стороны, при случайном упорядочении прибыли снижаются с самого начала (рис. 3.4.4).
Визуальная оценка способности критерия эффективно упорядочивать комбинации (рис. 3.4.4) должна теперь получить формализованное количественное выражение. Для этого зададимся целью построить идеальное упорядочение. Предположим, что интересующий нас критерий идеален, т.е. способен ранжировать комбинации таким образом, чтобы упорядочение по реализовавшейся в будущем прибыли полностью соответствовало упорядочению по значениям критерия, произведенному в момент оценки.
Другими словами, идеальным будем считать такой критерий, для которого упорядочение по его значениям совпадает с упорядочением по прибыли. Тогда показатель эффективности оцениваемого критерия должен выражать меру совпадения двух упорядочений, по критерию и по прибыли.
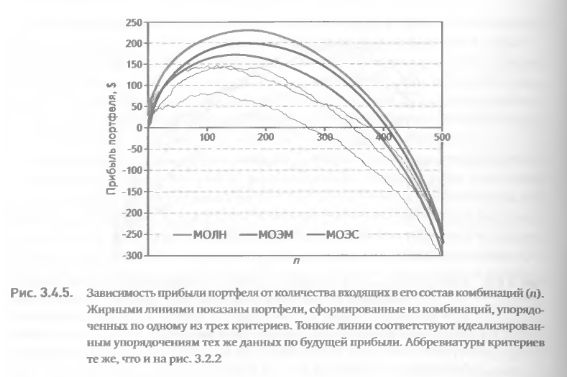
Идеализация критериев МОЛН, МОЭМ и МОЭС показана на рис. 3.4.5 тонкими линиями, полученными путем упорядочения комбинаций по значениям прибыли. Очевидно, что идеализации превосходят по качеству реальные упорядочения, достигнутые путем сортировок по критериям (жирные линии). Остается количественно выразить меру этого превосходства, что и будет являться показателем эффективности критерия.
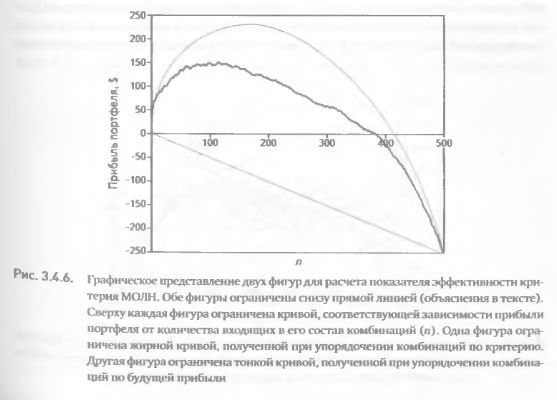
Начнем с графического представления идеи, лежащей в основе данного показателя эффективности. Обратимся вновь к зависимости прибыли портфеля от количества входящих в его состав комбинаций при двух видах упорядочения по значениям критерия МОЛН и по будущей прибыли (идеализация), Сосединим первую и последнюю точку двух графиков прямой линией (рис. 3.4.6). Первые и последние точки графиков всегда совпадают. Первая точка является стартовой и представляет собой «пустой» портфель (не включающий ни одной комбинации) с нулевой прибылью (он необходим для стандартизации и сравнимости двух упорядочений). Последняя точка соответствует портфелю, состоящему из всех без исключения комбинаций (в данном случае – из 500).
Поэтому, независимо от способа упорядочения, прибыль последнего портфеля будет неизменно равняться суммарной прибыли всех комбинаций, участвующих в анализе.
Соединив первые и последние точки прямой линией, получим две плоские фигуры с общим основанием (рис. 3.4.6). Первая фигура ограничена снизу прямой линией, а сверху–идеализированной кривой, соответствующей упорядочению по прибыли. Вторая фигура ограничена снизу той же прямой линией, а сверху – кривой, соответствующей упорядочению по критерию. Площадь первой фигуры всегда больше или равна площади второй. Чем больше площадь второй фигуры приближается к площади первой, тем выше качество критерия. В предельном случае совпадение двух площадей означает, что критерий достиг максимально возможной эффективности, поскольку в упорядочении комбинаций не было допущено ни одной ошибки.
Отношение площадей двух фигур можно рассматривать как количественное выражение показателя эффективности критерия, изменяющееся в пределах от 0 до 1. Рассчитать такой показатель можно следующим образом.
Пусть имеется исходное упорядочение комбинаций в порядке убывания их прибыли. Обозначим через it, it = 1,..., N порядковый номер комбинации. В нашем случае N= 500. Через p(k) обозначим величину прибыли комбинации к. Согласно упорядочению справедливо неравенство р(п) ≤ р(m) для любых номеров n и m таких, что n > m. Допустим, мы произвели оценку комбинаций по определенному критерию и упорядочили их по убыванию его значений. Обозначим через ik номер комбинации, попавшей на место к. Суммы
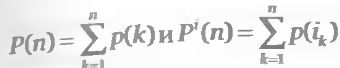
будут представлять собой прибыли двух портфелей, составленных из первых n комбинаций: Р(n) – для исходного упорядочения по убыванию прибыли и Рi (n) – для упорядочения по убыванию значений критерия. Легко видеть, что для любого n от 1 до N справедливо неравенство p(n) ≥ Рi (п), благодаря которому график прибылей портфеля для упорядочения по критерию при любом n не выше идеализированного графика. Обозначим через Pn = P(N) -Р i(n) суммарную прибыль полного портфеля из N комбинаций.
Тогда показатель эффективности критерия, выражающий отношение площадей указанных фигур, будет иметь следующий вид:

Рассчитаем показатель эффективности критерия для примера, иллюстрируемого рис. 3.4.6. Воспользовавшись формулой 3.4.1, получаем значение 1=0,72.
Данный показатель весьма чувствителен к общему количеству задействованных в анализе комбинаций (похожее явление было описано в разделе 3.3.1 для другого показателя эффективности, коэффициента детерминации). Продемонстрируем это графически, представив используемые в расчете площади на основе не 500, а меньшего количества комбинаций.
На рис. 3.4.7 показаны пары фигур, соответствующие 100, 200, 300, 400 и 500 комбинаций, задействованных в оценке эффективности критерия МОЛН. По мере сокращения количества комбинаций изменяются и соотношения площадей каждой пары фигур. Для 400 и 300 комбинаций показатель эффективности составил I = 0,59, для 200 комбинаций I = 0,63, а для 100 комбинаций I = 0,65. Хотя эти изменения не очень велики, практика показывает, что часто (в другие временные периоды, для других критериев и опционных стратегий) они бывают весьма существенны. Поэтому, основываясь на многочисленных исследованиях и результатах реальной торговли, мы рекомендуем использовать в анализе эффективности критерия, базирующемся на соотношении площадей, порядка 200-300 комбинаций.
|