|
Предположим, что исходное множество базовых активов В состоит из В акций, для каждой из которых мы намерены открыть торговую позицию, построенную по одной из двух возможных стратегий. Выбор стратегии производится на основе значений единственного критерия. Если значение критерия для комбинации, построенной по стратегии 1, больше значения критерия для комбинации, построенной по стратегии 2, то для этой акции позиция открывается по стратегии 1; в противном случае – позиция открывается по стратегии 2. Обозначим через К подмножество акций, для которых стратегия 1 была предпочтительней стратегии 2 (т. е. значения критерия для комбинаций, построенных по стратегии 1, были больше его значений для комбинаций, построенных по стратегии 2). К–число элементов подмножества К. Через П обозначим подмножество, состоящее из П акций, для которых результаты торговли по стратегии 1 были лучше результатов торговли по стратегии 2 (т. е. прибыль была больше или убыток меньше).
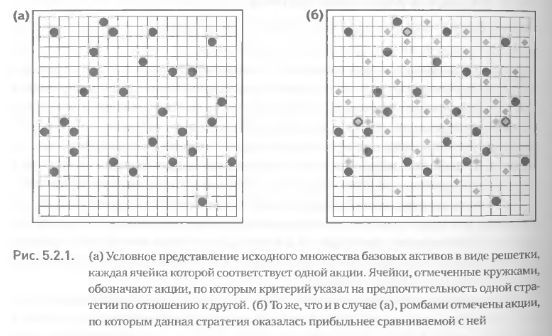
Для простоты рассмотрим пример, представив его в графическом виде. Предположим, что для 30 из 400 акций лучшей по критерию оказалась стратегия 1 (В = 400, К = 30). Представим исходное множество В в виде квадрата, разбитого на 400 ячеек, каждая из которых соответствует одной акции (рис. 5.2.1 (а)). Отметим кружками акции, для которых комбинации, построенные по стратегии 1, имели более высокое значение критерия, чем комбинации, построенные по стратегии 2, т.е. акции, относящиеся к подмножеству К (рис. 5.2.1 (а)). Теперь предположим, что определенное инвестиционным горизонтом время прошло и мы оценили прибыли и убытки каждой из двух стратегий для всех 400 акции. Акции, для которых комбинации, построенные по стратегии 1, оказались °лее прибыльными, чем комбинации, построенные по стратегии 2 (т. е. акции, относящиеся к подмножеству П), обозначим ромбами (рис. 5.2.1 (б)). В нашем примере П = 40. Теперь проанализируем рис. 5.2.1 (б), представляющий способность критерия выявить те акции, для которых применение стратегии 1 предпочтительнее применения стратегии 2.


Если бы наш критерий работал идеально, без единого «промаха», то во всех случаях, когда он указал на акции, для которых лучше использовать стратегию 1 (кружки), она действительно оказалась бы лучшей (ромбы), а для всех прочих акций – худшей. Тогда одни и те же ячейки были бы отмечены и кружками и ромбами. Но в реальной жизни идеал недостижим, поэтому в случаях, когда критерий промахивается, стратегия, лучшая по критерию, наделе оказывается хуже по прибыли (ячейки, отмеченные только кружками). И наоборот – стратегия, худшая по критерию, оказывается лучшей по прибыли (ячейки, отмеченные только ромбами). Теперь вернемся к рис. 5.2.1 (б). Мы видим, что только в трех случаях критерий сработал (три совпадения ромбов и кружков). Много это или мало? Корректнее было бы сформулировать вопрос иначе: скольких попаданий достаточно для заключения о работоспособности критерия?
Для ответа на этот вопрос пойдем от обратного – предположим, что критерий не работает, а совпадения кружков и ромбов случайны. В этом случае вероятность случайного попадания каждого ромба в ячейку, которая была отмечена кружком, равна отношению К /В. Отсюда следует, что при случайном распределении ромбов (а не вследствие того, что они «притягиваются» к ячейкам с кружками по причине эффективности критерия) математическое ожидание количества совпадений кругов и ромбов (КП) определяется формулой:

Подставляя значения из нашего примера, получаем 40 х 30/400 = 3. Ровно
только совпадений кружков и ромбов было в нашем примере (рис. 5.2.1 (б)).
То есть возможно, что количество совпадений в нашем примере является следствием случайности. Мы неспроста употребили оговорку «возможно». Дело в том, что формула 5.2.1 позволяет рассчитать лишь математическое ожидание количества совпадений. Это означает, что при наличии достаточно большого числа повторений эксперимента мы должны получить в среднем значение, равное расчетному по формуле 5.2.1. В нашем же примере было только одно наблюдение, результаты которого представлены на рис. 5.2.1 (б).
Рассмотрим другой пример. Предположим, что в другой день мы произвели оценку по критерию тех же 400 акций для тех же двух стратегий и получили следующие результаты: К = 35, П=20, КП = 15 (рис. 5.2.2). Мы видим существенное отличие рис. 5.2.1 (б) от рис. 5.2.2. Если в первом случае количество срабатываний критерия (количество совпадений кружков и ромбов) было невелико, то во втором случае оно стало заметным. И вновь возникает вопрос, достаточно ли велико число совпадений, чтобы сделать вывод об эффективности критерия?

По аналогии с первым примером воспользуемся формулой 5.2.1 для расчета математического ожидания количества совпадений, исходя из допущения о случайности совпадения. Получаем, что ожидаемое значение равно 1,75 (35 х х 20/400), в то время как реальное КП значительно выше (15). Таким образом, в данном примере у нас есть серьезные основания предположить, что полученное число совпадений возникло не случайно, а по причине выявления критерием предпочтительной стратегии для большинства акций.
Суммируя вышесказанное, приходим к заключению, что вывод об эффективности критерия можно сделать в том случае, когда КП > П х (К/В). Преобразуя неравенство, получаем формулу для расчета коэффициента эффективности критерия к (значения к, превосходящие 1, свидетельствуют о наличии предсказательной силы критерия):
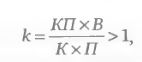
где В – количество оцениваемых акций (исходное множество базовых активов); К–количество акций, по которым критерий указал на предпочтительность данной стратегии по отношению к другим, сравниваемым с ней; П – количество акций, по которым данная стратегия оказалась прибыльнее, чем другие; КП – количество акций, попадающих одновременно и в множество К, и в множество П (в примерах КП – это совпадения кружков и ромбов; в реальной торговле акция попадает в множество КП, если для нее критерий указал предпочтительность данной стратегии по отношению к другим и это оказалось действительно так по показателю прибыли).
Используя формулу 5.2.2, мы можем рассчитать значение к для множества прошлых дат и таким образом получить достаточное количество наблюдений для достоверных выводов относительно отличия к от 1. Если тест Стьюдента покажет, что к > 1 на статистически значимом уровне, можно обоснованно утверждать, что критерий позволяет выбрать из многих опционных стратегий наилучшую для каждого отдельно взятого базового актива.
Для проведения статистического исследования мы сформировали исходное множество базовых активов из 500 акций США, имевших в феврале 2007 г. наибольший объем опционной торговли по контрактам с ближайшей датой экспирации. Были протестированы четыре стратегии: длинный стрэдл, короткий стрэдл, длинный календарный спред (покупка ближнего по дате колла и продажа дальнего по дате колла) и короткий календарный спред (продажа ближнего по дате колла и покупка дальнего по дате колла). Во всех случаях и для коллов, и для путов комбинации строились из контрактов с ближайшей датой экспирации по страйкам, наиболее близким к текущей цене акции, с равным количеством путов и коллов. То есть мы жестко зафиксировали алгоритм генерации комбинаций, чтобы его эффективность не влияла на оценку эффективности критерия в выборе стратегий. Для каждой акции была произведена оценка четырех комбинаций (по одной на каждую стратегию) по критерию «математическое ожидание прибыли по логнормальному распределению». Для каждой комбинации были определены прибыль или убыток на дату экспирации. И значение критерия, и величина прибыли (убытка) выражались как процент от маржевых требований. Для оценки были выбраны даты, выпадающие на третью неделю до ближайшей экспирации (например, для экспирации февраля 2007 г. это были даты 29,30 и 31 января, а также 1 и 2 февраля) в период с ноября 2000 г. по март 2007 г. (всего в анализе было задействовано 347 дат оценки, что позволило получить 347 значений к – достаточный материал для достоверного статистического анализа).
Стратегии сравнивались попарно в следующих сочетаниях:
-длинный стрэдл – короткий стрэдл
-длинный стрэдл – длинный календарный спред
-короткий стрэдл – короткий календарный спред
-длинный календарный спред – короткий календарный спред
Несмотря на то что тестирование четырех стратегий делает возможным шесть попарных сравнений, мы ограничились приведенными выше парами, поскольку отдельные стратегии в них являются либо конкурентами (короткий стрэдл – короткий календарный спред), либо антиподами (длинный стрэдл – короткий стрэдл). То есть выбор между ними является сложной и важной практической задачей, которую приходится ежедневно решать в реальной торговле.
Необходимо подчеркнуть, что для каждой пары необходимо провести два разных сравнительных анализа. Например, для пары длинный стрэдл – короткий стрэдл необходимо отдельно проанализировать эффективность критерия при выявлении акций, для которых стратегия «длинный стрэдл» более перспективна, чем стратегия «короткий стрэдл». После этого следует отдельно оценить способность критерия выявлять акции, для которых стратегия «короткий стрэдл» более перспективна, чем стратегия «длинный стрэдл». Хотя на первый взгляд это кажется лишней работой, на практике может оказаться, что один и тот же критерий хорошо отбирает акции, для которых стратегия 1 лучше стратегии 2, но плохо (или хуже) справляется с обратной задачей. Таким образом, анализ четырех названных выше пар стратегий на самом деле требует восьми попарных сравнений. Для каждого сравнения нами было получено 347 значений к (соответственно количеству дней оценки).
Теперь пришло время объяснить, почему мы назвали такой метод анализа ранговым. Дело в том, что для определения значения К, П и КП необходимо сначала определить принадлежность каждой акции к определенным рангам. Такая принадлежность определяется значениями критерия и реализовавшейся прибыли. Продемонстрируем это на конкретном примере. Рассмотрим данные, полученные на 1 марта 2007 г. Из 500 акций, оцененных на эту дату, мы выбрали первые 30 в алфавитном порядке, оценили значения критерия и реализовавшейся прибыли для стратегий «короткий стрэдл» и «длинный стрэдл» и провели анализ способности критерия определить комбинации, для которых первая стратегия предпочтительней второй. Результаты расчетов приведены в табл. 5.2.1. Для проведения рангового анализа рассчитаем величины разности между значением критерия для стратегии «короткий стрэдл» и его значением для стратегии «длинный стрэдл». Если разность >0, относим акцию к рангу а по критерию, в противном случае относим ее к рангу b. Далее вычислим разности между значением прибыли, полученной по стратегии «короткий стрэдл» и ее значением стратегии «длинный стрэдл». Аналогично, если разность >0, относим акцию к рангу а по прибыли, в противном случае – к рангу b. В табл. 5.2.1 для каждой акции указана ее принадлежность к рангам по критерию и по прибыли. (Корректнее было бы говорить, что к рангам относятся не акции, а комбинации, поскольку именно для них рассчитываются все значения параметров. Но так как для каждой акции построена только одна комбинация, мы будем использовать названия акций для обозначения относящихся к ним комбинаций).
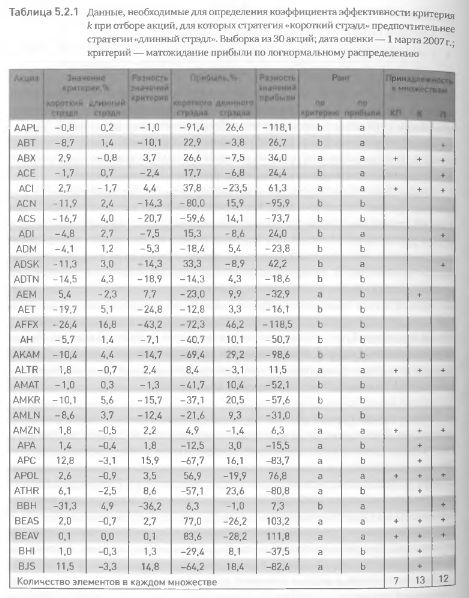
Акция, получившая ранг а и по критерию, и по прибыли (когда критерий но определил предпочтительность стратегии «короткий стрэдл»), попадает во все три множества К, П и КП. Акция, получившая ранг а по критерию и ранг b по прибыли (т. е. для этой акции критерий указал на предпочтительность стратегии «короткий стрэдл», но на практике это не подтвердилось), попадает только в множество К. Если акция получила ранг b по критерию и ранг а по прибыли (критерий не указал на предпочтительность стратегии «короткий стрэдл», но вновь «ошибся»), она попадает только в множество П. Если же акция получила ранг b и по критерию, и по прибыли (критерий не указал на предпочтительность стратегии «короткий стрэдл» и это подтвердилось на практике), она не попадает ни в одно множество, кроме В.
Определенная таким образом принадлежность каждой акции к одному или нескольким множествам обозначена в табл. 5.2.1 крестиками. Суммируя количество крестиков в каждом столбце, получаем: КП = 7, К = 13 и П = 12. Подставляя эти значения в формулу 5.2.2, можно рассчитать коэффициент эффективности критерия:
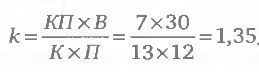
Полученное значение больше единицы, однако напомним, что этого примера недостаточно для обоснованного вывода об эффективности критерия. Необходимо получить большое количество коэффициентов к на выборках больших размеров. Именно к этому мы теперь и приступаем.
|