|
Практическое применение метода Парето нередко осложняется тем, что множество оптимальных точек оказывается недостаточно велико. Например, при оценке 1000 акций по двум критериям в большинстве случаев в множество Парето попадают не более пяти из них. В то же время, оценивая такое большое количество базовых активов, мы рассчитываем отобрать не менее 50 лучших, а зачастую даже больше.
В этом случае оказывается неизбежным переход от использования только оптимальных элементов к использованию субоптимальных. В качестве субоптимальных можно взять элементы, оптимальные для множества, построенного из исходного путем удаления из него уже найденных парето-оптимальных элементов. В предыдущем примере (табл. 7.2.1) мы определили, что из 30 акций три вошли в множество Парето. Если исключить эти три акции из рассмотрения и повторить процедуру на множестве оставшихся 27 элементов, то мы получим субоптимальное множество Парето.


Разумеется, мы не обязаны ограничиваться одним шагом такого рода и можем, найдя субоптимальные точки, удалить их из выборки, чтобы вновь найти оптимальные среди оставшихся. Такая процедура может продолжаться до тех пор, пока число найденных элементов не окажется достаточным. Следует, впрочем, помнить, что каждое повторение этой процедуры будет пополнять множество отобранных лучших акций новыми элементами, которые хуже предыдущих. Для того чтобы отличать оптимальные элементы от субоптимальных, а субоптимальные от последующих суб-субоптимальных, введем понятие «слоя». Элементы, найденные на первом этапе, назовем принадлежащими к слою 1; элементы, полученные после удаления попавших в слой 1 объектов, назовем принадлежащими к слою 2, затем к слою 3 и так далее.
В описанном выше примере акции VG, IDIX и MIR помещены в слой 1. Для построения второго слоя они удаляются из исходного множества. После упорядочения оставшихся 27 акций по критерию МОЛН на первом месте оказывается ELN (что указывает на ее принадлежность к множеству Парето слоя 2). После удаления всех элементов, доминируемых ELN, остаются только ONXX, SUP, GPS, KG, DNDN. Поскольку ONXX доминирует над SUP, GPS, KG и DNDN, то слой 2 будет состоять только из двух акций – ELN и ONXX. Для отыскания слоя 3 повторяем ту же процедуру: исключаем из 27 акций ELN и ONXX и находим паретовское множество среди оставшихся 25 акций. Слой 3 состоит из трех элементов – POZN, SUP и KG.
Из табл. 7.2.1 видно, что элементы, отнесенные ко второму и третьему слоям, хотя и доминируются элементами предшествующих слоев, однако имеют достаточно высокие значения критериев, и их целесообразно рассматривать наряду с Парето-оптимальными в собственном смысле (слой 1), если число элементов в множестве Парето недостаточно.
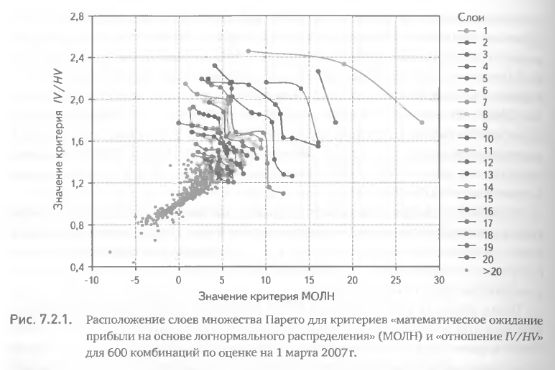
Таким образом, выбор наилучших комбинаций с применением одного слоя дает нам три потенциально лучших варианта, применение двух слоев – пять (3+2) вариантов, а применение трех слоев – восемь (3+2+3). Наглядное представление о множестве Парето и его послойном структурировании дает график, на одной оси которого откладывается значение одного критерия, а на второй оси – значение другого. Каждая точка на таком графике представляет собой опционную комбинацию, а ее координаты соответствуют значениям двух критериев. На рис. 7.2.1 показаны 20 паретовских слоев (а также все остальные точки множества) для пары критериев, использованных в табл. 7.2.1 (только в данном случае исходное множество состояло не из 30 комбинаций, а из 600). Хорошо видно, что первые слои располагаются в правой верхней части рисунка, т. е. в области, где значения обоих критериев достаточно велики. Последующие слои располагаются ниже и левее, а точки, не вошедшие в первые 20 слоев, лежат в области низких значений критериев.
Использование слоев позволяет расширить множество отбираемых комбинаций до желаемых пределов, хотя мы по-прежнему не имеем возможности задать точное их количество (в силу того, что не контролируем количество элементов, попадающих в каждый слой). Однако включение каждого дополнительного слоя означает открытие позиций с худшими показателями критериев, чем в предыдущих слоях. Это означает, что если используемые критерии действительно позволяют выбрать более перспективные для торговли комбинации (а иначе их применение лишено всякого смысла!), то увеличение количества слоев должно привести к снижению средней прибыли по всем комбинациям. Для того чтобы убедиться в этом, возьмем 13 пар критериев, но на этот раз не будем ограничиваться 30 базовыми активами, а для каждой пары критериев построим комбинации по 600 акциям. Воспользуемся той же стратегией и методикой построения комбинаций, которые были описаны выше в примере нахождения множества Парето (табл. 7.2.1).
Рассчитаем прибыль или убыток для каждой комбинации на дату истечения опционов и выразим их как процент от маржевых требований. Для каждой из 13 пар критериев получим последовательно 20 паретовских слоев. Рассчитаем средние прибыли/убытки (и стандартные отклонения) для всех комбинаций, попавших в n первых слоев (n пробегает от 1 до 20) для всех пар критериев. Результат представлен на рис. 7.2.2. По горизонтальной оси отложено количество использованных слоев, а по левой вертикальной – значение прибыли/убытка и стандартные отклонения. Очевидна тенденция падения средней прибыльности комбинаций с увеличением числа задействованных при отборе слоев. Однако не будем торопиться с выводами. Обратим внимание на то, что величина стандартного отклонения (мера изменчивости результата) также падает с ростом числа слоев. По правой оси на рис. 7.2.2 отложено отношение среднего к стандартному отклонению – вариант коэффициента Шарпа. Этот коэффициент является общепризнанным показателем, учитывающим одновременно и прибыльность, и ее изменчивость. Из рис. 7.2.2 следует, что коэффициент Шарпа неуклонно растет с увеличением количества слоев. Это объясняется тем, что в силу увеличения количества комбинаций повышается диверсификация портфеля и, как следствие, снижается его риск. Таким образом, решение вопроса о количестве используемых слоев является результатом компромисса между стремлением максимизировать прибыль и минимизировать риск создаваемого портфеля.
Итак, мы убедились, что увеличение количества слоев приводит к снижению средней прибыли вследствие роста числа используемых для торговли комбинаций.

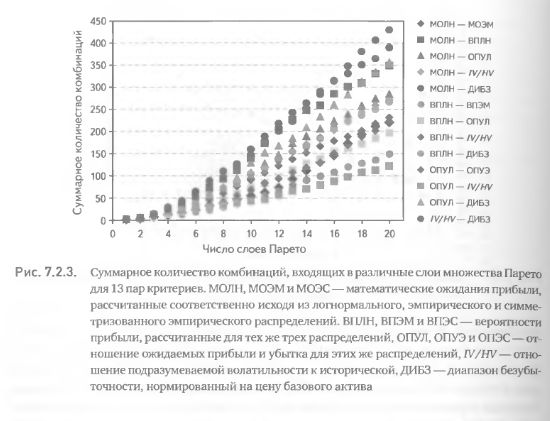
В этой связи интересно рассмотреть, как именно увеличение количества слоев влияет на темпы роста числа отбираемых комбинаций. Для каждой из 13 пар критериев определим количество комбинаций, вошедших в слой 1,2... и до 20. На рис. 7.2.3 видно, что суммарное количество комбинаций стремительно увеличивается с добавлением каждого последующего слоя. На 10-м слое их число колеблется от 50 до 100, а на 20-м – от 110 до 440. Столь широкий диапазон разброса означает, что для одних пар критериев рост количества отбираемых комбинаций с добавлением новых слоев происходит умеренными темпами; для других же пар критериев применение дополнительных слоев приводит к очень быстрому росту числа отбираемых комбинаций. Чем это объясняется? Дело в том, что большинство критериев в той или иной степени коррелируют между собой, т. е. большим значениям одного критерия соответствуют большие значение другого. Дальше мы покажем, что чем сильнее скоррелированы два критерия, тем меньшее число комбинаций попадает во множество Парето. Отсюда следует, что столь большая разница в количестве комбинаций, отбираемых по разным парам критериев (рис. 7.2.3), объясняется различной степенью скоррелированности последних.
Мы уделили этому вопросу столь пристальное внимание не случайно, ведь количество акций, отбираемых для торговли, имеет большое практическое значение. С одной стороны, чем меньше выбрано базовых активов, тем лучше показатели критериев и тем больше ожидаемая прибыль. С другой же стороны, для управления рисками необходима разумная степень диверсификации, что требует выбора большего количества акций. В поисках компромисса между этими двумя факторами мы вынуждены оптимизировать количество используемых паретовских слоев и при этом учитывать зависимость темпов роста числа базовых активов от уровня корреляции между критериями.
|