20.9. Корреляция между дефолтами

Термин корреляция между дефолтами (default correlation) характеризует возможность одновременного дефолта двух компаний. Существует большое количество причин, объясняющих такую корреляцию. Две компании, работающие в одной и той же отрасли промышленности или в одном и том же географическом регионе, подвергаются одинаковым воздействиям внешних событий и могут одновременно испытывать финансовые затруднения. Кроме того, вследствие разных экономических условий, как правило, средняя вероятность дефолта в разные годы может быть разной. Дефолт одной компании может повлечь за собой дефолт другой – эффект смягчения кредитного риска описан в разделе 20.5. Корреляция между дефолтами означает, что кредитный риск невозможно полностью исключить за счет диверсификации и он является основной причиной, по которой риск-нейтральная вероятность дефолта превышает реальную (см. раздел 20.5).

Корреляция между дефолтами играет важную роль при определении распределения вероятностей потерь вследствие дефолта, которые может понести портфель, состоящий из контрактов с разными контрагентами. Существует два типа моделей, предложенных исследователями для оценки корреляции между дефолтами: модели редуцированных форм (reduced-form models) и структурные модели (structural models).

Модели редуцированных форм основаны на предположении, что уровни риска у разных компаний подчиняются стохастическим процессам и коррелируют с макроэкономическими показателями. Если уровень риска у компании А высок, то уровень риска у компании В также, вероятно, будет высок. Это порождает корреляцию между дефолтами компаний А и В.

Модели редуцированных форм весьма привлекательны с математической точки зрения и отражают тот факт, что экономические циклы порождают корреляцию между дефолтами. Их можно согласовать с вероятностями дефолтов, наблюдаемыми на практике, а также с риск-нейтральными вероятностями дефолтов, вычисленных по ценам облигаций. Их основной недостаток заключается в том, что получаемый диапазон коэффициентов корреляции между дефолтами является узким. Даже если между уровнями риска существует идеальная корреляция, соответствующая корреляция между дефолтами в любой выбранный период времени, как правило, является очень низкой. В некоторых ситуациях это может создать проблемы. Например, если две компании действуют в одной и той же отрасли промышленности или в одной и той же стране либо финансовое благополучие одной компании существенно зависит от благосостояния другой, то корреляция между дефолтами этих компаний должна быть высокой, а не низкой. Это противоречие можно снять, распространив модель на ситуации, в которых возможны крупные скачки уровней риска.

Структурные модели основаны на идее, аналог которой рассматривался в разделе 20.6. Если стоимость активов компании падает ниже определенного уровня, то она объявляет дефолт. Корреляция между дефолтами компаний A и В вводится на основе предположения, что стохастический процесс, описывающий поведение активов компании А, коррелирует со стохастическим процессом, описывающим поведение активов компании В. Преимущество структурных моделей над моделями редуцированных форм заключается в том, что корреляцию между дефолтами можно сделать сколь угодно высокой. Их основной недостаток состоит в том, что они связаны с большим объемом вычислений.

Модель гауссовых пакетов

Одной из моделей редуцированных форм, получивших широкое распространение, стала модель гауссовых пакетов (Gaussian copula model), позволяющая вычислить момент дефолта. С помощью этой модели можно вычислить корреляцию между моментами объявления дефолтов двумя разными компаниями. В основе этой модели лежит неявное предположение, что все компании рано или поздно объявят дефолт. Однако в любом приложении этой модели нас обычно интересует только вероятность дефолта в течение следующего года или следующих пяти и десяти лет. Таким образом, в центре нашего внимания находится только левый хвост распределения моментов объявления дефолта.

Эту модель можно использовать в сочетании как с реальной, так и риск-нейтральной вероятностью дефолта. Левый хвост распределения реальных вероятностей моментов объявления дефолтов можно оценить на основе данных, публикуемых рейтинговыми агентствами (примером такой информации является табл. 20.1). Левый хвост распределения риск-нейтральных вероятностей моментов объявления дефолтов можно оценить на основе цен облигаций, используя подход, изложенный в разделе 20.4.

Обозначим через t₁ момент дефолта компании 1, а через t₂ – момент дефолта компании 2. Если распределения вероятных значений t₁ и t₂ являются нормальными, то можно предположить, что совместное распределение переменных t_i и t₂ также является нормальным. Оказывается, распределение вероятных моментов времени дефолта любой компании даже приближенно не является нормальным. Именно поэтому необходима модель гауссовых пакетов. Преобразуем переменные t₁ и t₂ в новые переменные х₁ и x₂, используя следующие функции.

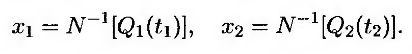
Здесь Q₁ и Q₂ – интегральные распределения вероятных значений моментов t₁ и t₂ соответственно, a N^-1 – функция, обратная к интегральному нормальному распределению (т.е. если v = N(u), то u = N^-1(v)). Эти преобразования представляют собой отображения перцентилей. Точка, соответствующая пятому перцентилю распределения переменной t₁, преобразуется в точку х₁ = –1,645, которая представляет собой точку, соответствующую пятому перцентилю стандартного нормального распределения. Аналогично точка, соответствующая десятому перцентилю распределения переменной t₁, преобразуется в точку х₁ = –1,282, которая представляет собой точку, соответствующую десятому перцентилю стандартного нормального распределения и т.д. Преобразование переменной t₂ в переменную x₂ осуществляется точно так же.

По построению переменные x₁ и x₂ имеют нормальное распределение с нулевым математическим ожиданием и единичным стандартным отклонением. Предположим, что совместное распределение переменных х₁ и x₂ является нормальным, а корреляция между ними равна ρ₁₂. Это предположение порождает так называемый гауссовый пакет (Gaussian copula). Оно является удобным, поскольку в этом случае совместное распределение случайных величин t₁ и t₂ и единственный коэффициент корреляции ρ₁₂ полностью определяют интегральные распределения вероятностей дефолтов Q₁ и Q₂ в моменты t₁ и t₂.

Привлекательность подхода, основанного на использовании гауссовых пакетов, заключается в том, что его легко распространить на несколько компаний. Предположим, что мы рассматриваем п компаний, а t_i – момент дефолта i-й компании. Преобразуем каждую переменную t_i в переменную x_i, имеющую стандартное нормальное распределение. Это преобразование представляет собой отображение перцентилей, имеющее вид

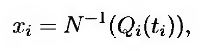
где Q_i – интегральное распределение вероятностей для переменной t_i. Предположим теперь, что переменная x_i имеет многомерное нормальное распределение. Корреляция между дефолтами в моменты t_i и t_j измеряется как корреляция между переменными x_i и x_j. Эту величину называют пакетной корреляцией (copula correlation).

Модель гауссовых пакетов оказывается полезной при описании структуры корреляции между переменными, не имеющими нормального распределения. Она позволяет оценивать корреляционную структуру каждой переменной по отдельности на основе их маргинальных распределений. Несмотря на то что сами переменные не имеют многомерного нормального распределения, этот подход предполагает, что после преобразования каждой переменной они имеют многомерное нормальное распределение.

Пример 20.3

Предположим, что мы желаем смоделировать дефолты 10 компаний на протяжении следующих пяти лет. Пакетная корреляция между любыми парами компаний равна 0,2. Интегральная вероятность дефолта каждой компании на протяжении следующих одного, двух, трех, четырех и пяти лет равна 1%, 3%, 6%, 10% и 15% соответственно. Если для моделирования используются гауссовы пакеты, то из генеральной совокупности чисел, имеющих многомерное нормальное распределение, извлекаются величины x_i, где 1 ≤ i ≤ 10, корреляция между которыми равна 0,2. Затем переменные x_i преобразуются в переменные t_i, представляющие собой выборочные моменты дефолтов. Если выборочное значение, извлеченное из генеральной совокупности с нормальным распределением, меньше N^-1(0,01) = –2,33, то дефолт происходит на протяжении первого года; если эта величина лежит между числами –2,33 и N^-1(0,03) = –1,88, то дефолт происходит на протяжении второго года; если эта величина лежит между числами –1,88 и N^-1(0,06) = –1,55, то дефолт происходит на протяжении третьего года; если эта величина лежит между числами –1,55 и N^-1(0,10) = –1,28, то дефолт происходит на протяжении четвертого года; если эта величина лежит между числами -1,28 и N^-1(0,15) = –1,04, то дефолт происходит на протяжении пятого года. Если же выборочное значение больше –1,04, дефолт вообще не происходит.

Применение факторных моделей для описания корреляционной структуры

Чтобы избежать определения корреляции между переменными x_i и x_j для каждой пары компаний i и j в рамках модели гауссовых пакетов, часто используется однофакторная модель. В основе этой модели лежит предположение, что

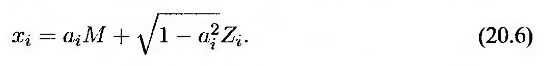
М – общий фактор, влияющий на дефолты всех компаний, a Z_i – фактор, характерный только для компании i. Переменные М и Z_i не зависят друг от друга и имеют нормальное стандартное распределение. Параметры a_i лежат в диапазоне от -1 до +1. Корреляция между переменными x_i и x_j равна a_ia_j.

Пусть вероятность того, что компания i объявит дефолт в конкретный момент времени Т, равна Q_i(T). В рамках модели гауссовых пакетов дефолт происходит, если N(x_i) < Q_i(T), т.е. х_i < N^-1[Q_i(T)]. Учитывая формулу (20.5), это условие можно переписать как

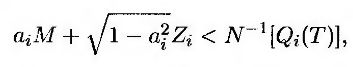
или

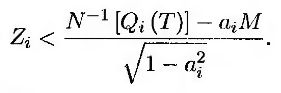
Следовательно, условную вероятность дефолта, зависящую от фактора М, можно выразить следующим образом.

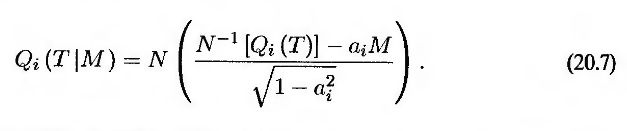
Частным случаем однофакторной модели гауссовых пакетов является модель, в которой распределение вероятностей дефолта для всех i одинакова, а корреляция между переменными x_i и x_j для любой пары i и j остается неизменной. Предположим, что Q_i(T) = Q(T) для всех i, а общая корреляция равна ρ. Тогда a_i = √ρ при всех значениях i, а уравнение (20.7) принимает вид

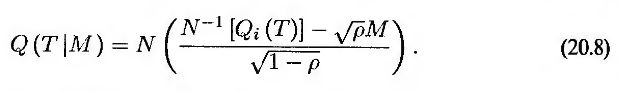
Коэффициент биномиальной корреляции

Альтернативным средством измерения корреляции, используемым рейтинговыми агентствами, является коэффициент биномиальной корреляции (binomial correlation measure). Рассмотрим это понятие для компаний A и B.

1. Переменная равна единице, если компания А объявляет дефолт между нулевым моментом времени и моментом Т, и нулю – в противном случае.

2. Переменная равна единице, если компания В объявляет дефолт между нулевым моментом времени и моментом Т, и нулю – в противном случае.

Эта величина равна

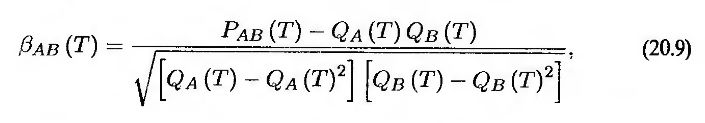
где Р_АВ(Т) – совместная вероятность того, что компании A и B объявят дефолт на промежутке времени между нулевым моментом и моментом T. Как и прежде, величина Q_B(T) представляет собой интегральную вероятность того, что компания А объявит дефолт в момент T, a Q_B(T) является интегральной вероятностью того, что компания В объявит дефолт в момент Т. Величина β_АВ,(Т) зависит от длины рассматриваемого промежутка времени Т. Как правило, при возрастании величины Т она возрастает.

Из определения модели гауссовых пакетов следует, что Р_АВ(Т) = M[x_A(t), x_B(t);ρ_AB], где х_A(Т) = N^-1(Q_A(T)) и х_B(Т) = N^-1(Q_B(T)) – преобразованные моменты дефолтов компаний A и B, а ρ_AB – оценка корреляции дефолтов между переменными A и B в модели гауссовых пакетов. Здесь значения функции М(а, b; ρ) представляют собой вероятность того, что первая переменная меньше числа а, а вторая переменная меньше числа b, если коэффициент корреляции между этими переменными равен ρ, а сами переменные имеют двухмерное стандартное нормальное распределение.

Отсюда следует, что

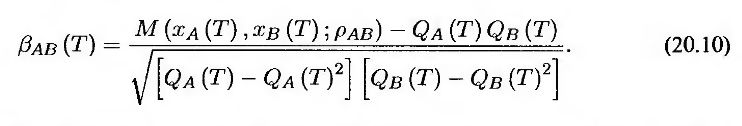
Таким образом, если величины Q_A(T) и Q_B(T) известны, то коэффициент β_AB можно вычислить по величине ρ_AB и наоборот. Как правило, величина ρ_AB намного больше, чем ρ_AB(T). Это подчеркивает тот важный момент, что величина корреляции зависит от способа ее вычисления.

Пример 20.4

Предположим, что вероятности дефолтов компаний A и B на протяжении года равны 1%. В таком случае x_A(1) = x_B(1) = –2,326. Если ρ_AB = 0,20, то М(X_A(1), X_B(1), ρ_AB) = 0,000337, а из формулы (20.10) следует, что ρ_AB(Т) = 0,024, где Т = 1.