Приложение 25.1. Обобщение леммы Ито на ситуацию с несколькими источниками неопределенности

В данном приложении доказываются лемма Ито и формула (25.13), связывающая избыточную доходность и рыночную стоимость риска в ситуации с несколькими источниками неопределенности.

Лемма Ито для функции, зависящей от нескольких переменных

Как показано в главе 12, лемма Ито описывает процесс, которому подчиняется функция, зависящая от одной стохастической переменной. В данном приложении формулируется обобщенный вариант леммы Ито для процесса, описывающего поведение функции, зависящей от нескольких стохастических переменных.

Предположим, что функция f зависит от n переменных х₁, x₂, ..., х_n и времени t. Допустим также, что переменные х_i подчиняются процессу Ито с мгновенным дрейфом а_i и мгновенной дисперсией b²_i, 1 ≤ i ≤ п, т.е.

где dz_i, 1 ≤ i ≤ n – винеровский процесс. Каждый коэффициент а_i и b_i может зависеть от всех переменных x_i и времени t. Разложение функции f в ряд Тейлора имеет следующий вид.

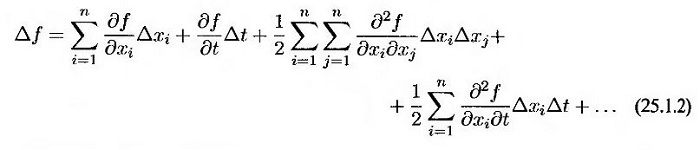
Дискретный аналог уравнения (25.1.1) выглядит так.

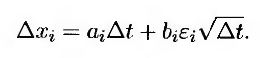
Здесь величина ε_i является выборочным значением, извлеченным из генеральной совокупности со стандартизованным нормальным распределением. Коэффициент корреляции ρ_ij между величинами dz_i и dz_j равен коэффициенту корреляции между величинами ε_i и ε_j. В главе 12 показано, что

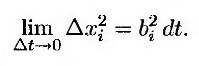
Аналогично

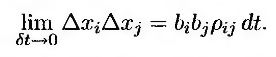
При Δt → 0 первые три члена разложения величины Δf в уравнении (25.1.2) имеют первый порядок по Δt. Все остальные члены содержат множители Δt в более высокой степени. Следовательно,

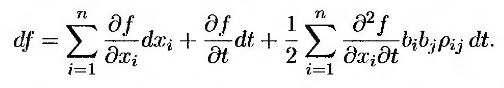
Этот результат представляет собой обобщенный вариант леммы Ито. Подставляя в этой выражение формулу (25.1.1), приходим к следующему равенству.

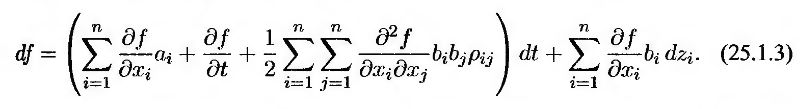
Рассмотрим альтернативное доказательство расширенной леммы Ито. Предположим, что функция f зависит от единственной переменной x, поведение которой, в свою очередь, определяется несколькими винеровскими процессами.

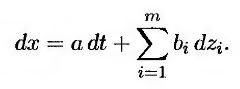
В таком случае

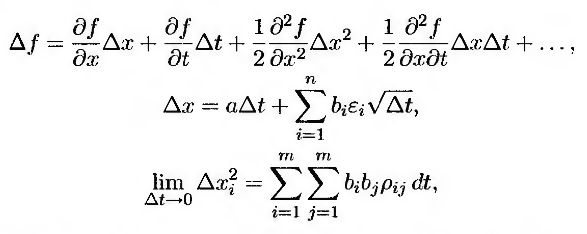где p_ij – коэффициент корреляции между величинами dz_i и dz_j. Отсюда следует, что

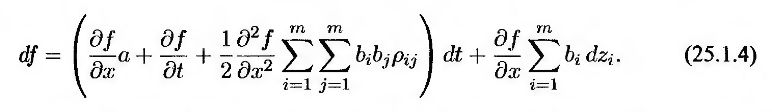
В заключение, рассмотрим более общий вариант, в котором функция f зависит от переменных x_i, 1 ≤ i ≤ n, и

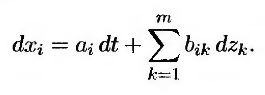
Аналогичный анализ показывает, что

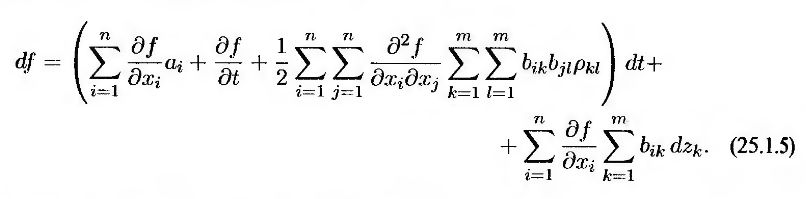
Доходность ценной бумаги, зависящей от нескольких источников неопределенности

В разделе 25.1 доказана формула, связывающая избыточную доходность с риском при единственном источнике неопределенности. Перейдем к доказательству этой формулы для ситуации, в которой существует несколько источников неопределенности.

Рассмотрим n стохастических переменных, описываемых винеровскими процессами, и n + 1 ценных бумаг; стоимость которых зависит от нескольких или всех n стохастических переменных. Обозначим через f_j стоимость j-й ценной бумаги, где 1 ≤ j ≤ n + 1. Предположим, что рассматриваемые ценные бумаги не приносят дивидендов или другого дохода. Отсюда следует, что ценная бумага описывается стохастическим процессом

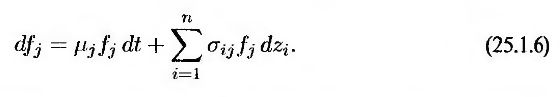
Поскольку количество ценных бумаг равно п + 1, а количество винеровских процессов равно п, можно сформировать инвестиционный портфель П, свободный от риска. Пусть k_j – количество j-й ценной бумаги в портфеле. Отсюда следует, что

Величины k_j необходимо выбрать так, чтобы стохастические компоненты доходности ценных бумаг были исключены. С учетом уравнения (25.1.6) это значит, что

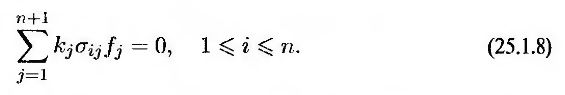
Доходность портфеля выражается формулой

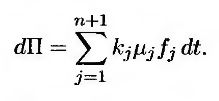
Стоимость создания портфеля равна

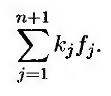
Если арбитражные возможности отсутствуют, доходность портфеля должна быть равной безрисковой процентной ставке, так что

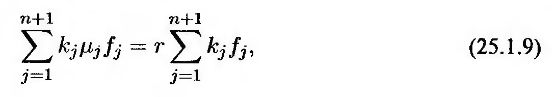
т.е.

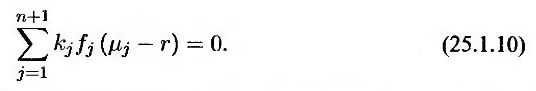
Уравнения (25.1.8) и (25.1.10) можно рассматривать как систему, состоящую из n + 1 линейных однородных уравнений относительно неизвестных величин k_j, которые не могут одновременно равняться нулю. Из хорошо известной теоремы линейной алгебры следует, что уравнения (25.1.8) и (25.1.10) являются совместными тогда и только тогда, когда при всех значениях индекса j выполняется соотношение

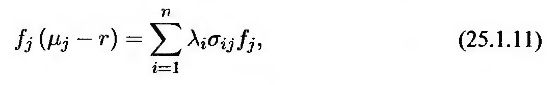
или

для некоторых переменных λ_i (1 ≤ i ≤ n), зависящих только от переменных состояния и времени. Отбрасывая индекс j, приходим к выводу, что для любой ценной бумаги f, зависящей от n стохастических переменных, выполняется соотношение

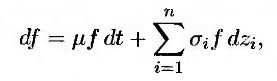
где

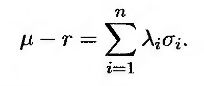
Это доказывает формулу (25.13).