26.2. Облигационные опционы

Облигационный опцион (bond option) – это опцион на покупку или продажу облигации в определенный день по установленной цене. Кроме внебиржевого рынка, облигационные опционы часто сопровождают выпуск облигаций, чтобы повысить их привлекательность для потенциальных покупателей (такие опционы называются внутренними (embedded)).?

Внутренние облигационные опционы

Примером внутреннего облигационного опциона (embedded bond option) является отзывная облигация (callable bond). Это – облигация, содержащая условия, позволяющие эмитенту в будущем выкупить ее обратно по заранее установленной цене в определенный момент. Владелец такой облигации продает эмитенту опцион на ее покупку. Цена исполнения этого опциона представляет собой заранее установленную цену, по которой облигация должна быть продана эмитенту. Отзывные облигации, как правило, нельзя выкупать на протяжении первых нескольких лет после ее выпуска. (Этот интервал времени называется периодом блокировки (lock out period).) Затем стоимость опциона со временем обычно падает. Например, при выпуске 10-летней отзывной облигации на протяжении первых двух лет эмитент может не иметь привилегий. После этого эмитент может получить право выкупить облигацию: на третий и четвертый годы – за 110 долл., на пятый и шестой – за 107,5 долл., на седьмой и восьмой – за 106 долл., а на девятый и десятый – за 103 долл. Стоимость опциона на покупку облигации отражается на ее купонной доходности. Облигации, допускающие досрочный выкуп, обычно имеют более высокую доходность, чем остальные.

Еще одним примером внутреннего опциона является облигация с правом досрочного погашения (puttable bond). Такая облигация содержит условия, позволяющие владельцу требовать досрочного погашения облигации по заранее установленной цене в определенные моменты времени. Владелец такой облигации вместе с ней покупает опцион на ее продажу. Поскольку опцион на продажу облигации повышает ее стоимость, такие облигации имеют более низкую купонную доходность, чем остальные. Простым примером облигации с правом досрочного отзыва является 10-летняя облигация, владелец которой имеет право досрочно погасить ее в конце пятого года. (Такие облигации иногда называются сжимаемыми (retractable).)

Заемные и депозитные инструменты также часто содержат внутренние облигационные опционы. Например, пятилетний депозит с фиксированной ставкой, который в любой момент можно закрыть без штрафных санкций, содержит американский опцион на продажу облигации. (Депозит – это облигация, владелец которой имеет право вернуть ее финансовой организации в любой момент.) Авансовые привилегии по обычным и ипотечным займам также эквивалентны опционам на покупку облигаций.

В заключение отметим, что любое соглашение о выдаче денежной ссуды, заключенное банком или другой финансовой организацией, представляет собой опцион на продажу облигации. Рассмотрим, например, ситуацию, в которой банк устанавливает для своих потенциальных заемщиков пятилетнюю процентную ставку на уровне 12% и утверждает, что эта ставка будет действовать в течение следующих двух месяцев. Фактически, клиент банка получает право в любой момент на протяжении ближайших двух месяцев продать финансовой организации пятилетнюю облигацию с 12%-ным купоном по ее номинальной стоимости.

Европейские облигационные опционы

Многие внебиржевые облигационные опционы и некоторые опционы, сопровождающие выпуск облигаций, являются европейскими. Рассмотрим теперь стандартные рыночные модели, используемые при оценке европейских опционов.

Как правило, в основе таких моделей лежит предположение о том, что цена облигации в момент ее погашения имеет логнормальное распределение. В этом случае для вычисления цены опциона можно применять формулы (26.1) и (26.2), заменяя величину F₀ форвардной ценой облигации F_B. Как указано в разделе 26.1, переменная σ_B выбирается так, чтобы величина σ_B√T была стандартным отклонением логарифма цены облигации в момент завершения опциона. Таким образом, формулы для вычисления европейского облигационного опциона имеют следующий вид.

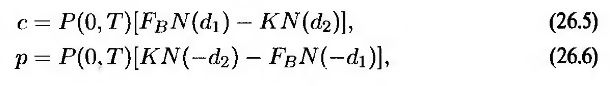
где

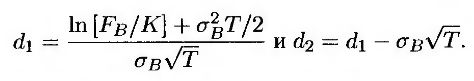
Как указано в разделе 5.5, величину E_B можно вычислить по формуле

где В₀ – цена облигации в нулевой момент времени, a I – текущая стоимость купонов, погашаемых на протяжении всего срока обращения облигации. В этой формуле как цена спот, так и форвардная цена облигации являются наличными ценами (cash prices), а не котировками. Разница между наличными ценами и котировками разъясняется в разделе 6.2.

Цена исполнения К в формулах (26.5) и (26.6) должна быть наличной. Таким образом, чтобы выбрать правильное значение К, необходимо точно учесть условия опциона. Если цена исполнения представляет собой денежную сумму, на которую обменивается облигация в момент ее погашения, то величину К следует установить равной этой цене исполнения. Если же цена исполнения представляет собой котировку, применяемую при исполнении опциона, величину К следует установить равной сумме цены исполнения и дохода, накопленного к моменту погашения. Трейдеры называют котировочную цену облигации “чистой”, а наличную цену – “грязной”.?

Пример 26.1

Рассмотрим 10-месячный европейский опцион на покупку 9,75-летней облигации с номинальной стоимостью 1 000 долл. (В момент исполнения опциона до погашения облигации останется 8 лет и 11 месяцев.) Допустим, что текущая наличная цена облигации равна 960 долл., цена исполнения опциона равна 1 000 долл., 10-месячная безрисковая процентная ставка равна 10% годовых, а волатильность форвардной цены облигации за 10 месяцев равна 9% в год. Облигация предусматривает купонные выплаты: каждые полгода – 10%, а через три и девять месяцев – по 50 долл. (Это значит, что накопленный доход равен 25 долл., а котировочная цена облигации равна 935 долл.) Предположим, что трех- и девятимесячная безрисковые процентные ставки равны 9,0 и 9,5% соответственно. Следовательно, текущая стоимость купонных выплат равна

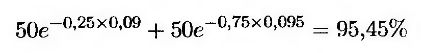
т.е. 95,45 долл. Из формулы (26.7) следует, что форвардная цена облигации равна

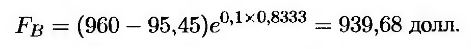
1. Если цена исполнения равна наличной цене, которая выплачивается в момент погашения облигации, то параметры в формуле (26.5) устанавливаются следующим образом: F_B = 939,68, K = 1000, Р(0, Т) = 50е^-0,1x(10/12) = = 0,9200, σ = 0,09 и Т = 10/12. Стоимость опциона “колл” равна 9,49 долл.

2. Если цена исполнения равна котировочной цене, которая выплачивается в момент погашения облигации, то к величине К следует добавить доход, накопленный за один месяц, поскольку исполнение опциона происходит через один месяц после купонной выплаты. Следовательно,

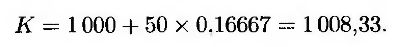
Значения других параметров в формуле (26.5) остаются прежними (т.е. F_B = 939,68, K = 1000, Р(0, Т) = 50е^-0,1x(10/12) = 0,9200, σ = 0,09 и Т = 0,8333). Цена опциона равна 7,97 долл.

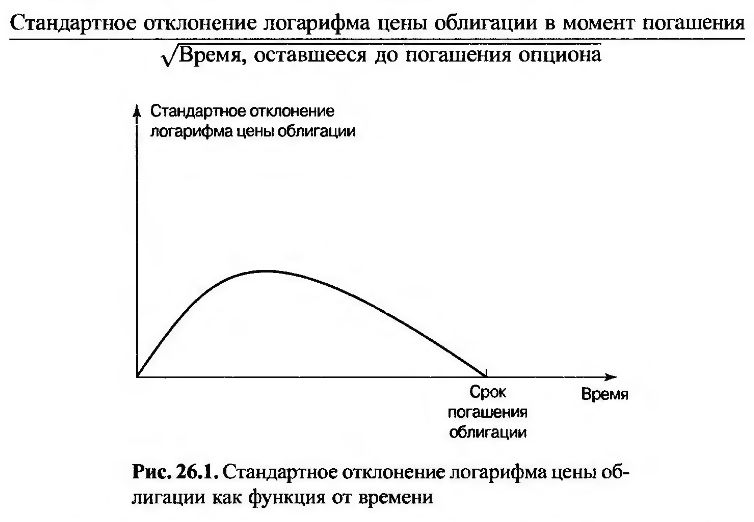
Как показано на рис. 26.1, стандартное отклонение логарифма цены облигации со временем изменяется. В текущий момент стандартное отклонение равно нулю, поскольку относительно сегодняшней цены облигации нет никакой неопределенности. В момент погашения облигации стандартное отклонение ее цены также равно нулю, поскольку нам известно, что в этот момент ее цена равна номинальной стоимости. Между текущим моментом и сроком погашения облигации стандартное отклонение сначала растет, а потом падает. Волатильность σ, которая используется при оценке европейского опциона на покупку или продажу облигации, вычисляется по следующей формуле.

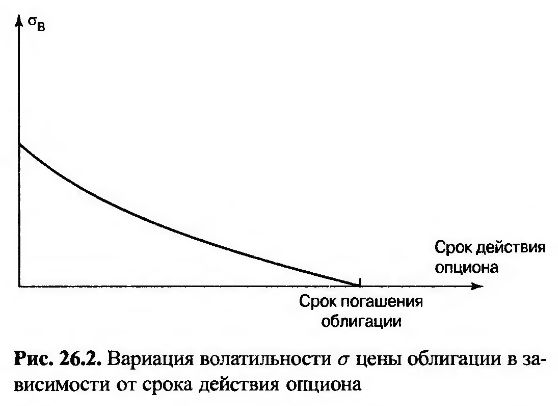
Типичная форма волатильности σ как функции от срока действия опциона представлена на рис. 26.2.

Волатильности доходности

В качестве волатильности, характеризующей изменчивость облигационного опциона, часто используется волатильность доходности, а не цены. Для преобразования волатильности котировочной доходности в волатильность цены используется понятие дюрации, изложенной в главе 4. Предположим, что D – модифицированная дюрация (modified duration). Зависимость между изменением форвардной цены облигации ΔF_B и изменением ее форвардной доходности Δ_yF имеет следующий вид.

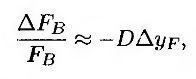
или

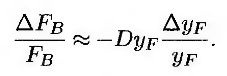
отклонения относительных изменений величины переменной. Следовательно, это уравнение предполагает, что волатильность σ_B форвардной цены облигации, используемую в модели Блэка, можно связать с волатильностью σ_y форвардной доходности облигации с помощью следующего приближенного соотношения.

Здесь y₀ – начальное значение переменной y_F. При выборе волатильности доходности для облигационного опциона, как правило, используется неявное предположение, что ее можно преобразовать в волатильность цены, используя формулу (26.8), и что для вычисления цены облигации эту волатильность можно использовать совместно с формулами (26.5) и (26.6). Предположим, что модифицированная дюрация облигации, лежащей в основе опциона “колл”, в момент его исполнения равна пяти годам, форвардная доходность равна 8%, а волатильность форвардной доходности, установленная брокером, равна 20%. Это значит, что рыночная цена опциона, соответствующая котировке брокера, равна цене, вычисленной по формуле (26.5), в которой волатильность σ равна

т.е. 8% годовых. Как следует из рис. 26.2, форвардная волатильность облигации зависит от рассматриваемого опциона. В то же форвардная волатильность доходности, определенная выше, является постоянной. По этой причине трейдеры предпочитают работать именно с ней.

Для вычисления цены европейского облигационного опциона с помощью модели Блэка можно использовать рабочий лист Bond Options в программе Deriva-Gem, выбрав пункт Black-European в раскрывающемся списке Pricing Model. Затем следует ввести волатильность доходности, вычисленную так, как показано выше. В качестве цены исполнения необходимо выбрать наличную или котировочную цену исполнения.

Пример 26.2

Рассмотрим европейский опцион на продажу десятилетней облигации с номинальной стоимостью, равной 100. Купонные выплаты осуществляются раз в полгода в размере 8%. Продолжительность опциона равна 2,25 года, а его цена исполнения равна 115. Волатильность форвардной доходности равна 20%. Кривая нулевой доходности является плоской и проходит на уровне 5% при непрерывном начислении. Применение программы DerivaGem показывает, что котировочная цена облигации равна 122,84. Если в качестве цены исполнения используется котировочная цена, то стоимость опциона равна 2,37. Если же в качестве цены исполнения используется наличная цена, стоимость опциона равна 1,74 долл. (Обратите внимание на то, что результаты вычисления с помощью программы DerivaGem могут не совпадать с результатами вычислений, выполненными вручную, поскольку в программе DerivaGem заложено предположение, что год состоит из 365 дней и она округляет время до ближайшего целого числа дней; см. задачу 26.16.)

Теоретическое обоснование модели

В разделе 25.4 рассмотрены гипотезы, альтернативные обычным риск-нейтральным предположениям, используемым при оценке деривативов. Одной из этих гипотез являются форвардные риск-нейтральные условия относительно облигации с нулевым купоном, срок обращения которой истекает в момент Т. В частности, при указанных предположениях там были доказаны следующие утверждения.

1. Текущая стоимость любой ценной бумаги равна ее ожидаемой стоимости в момент Т, умноженной на цену облигации с нулевым купоном в этот момент.

2. Ожидаемая цена любой ценной бумаги в момент Т равна ее форвардной цене (формула (25.21)).

Первый из этих результатов означает, что цена опциона на покупку облигации, срок действия которого завершается в момент Т, равна

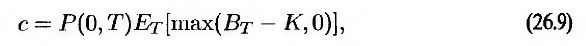
где В_T – цена облигации в момент Т, а E_T – математическое ожидание переменной в форвардных риск-нейтральных условиях относительно облигации с нулевым купоном, срок обращения которой истекает в момент Т. Из второго утверждения следует, что

Предполагая, что цена облигации имеет логнормальное распределение и стандартное отклонение логарифма цены облигации равно σ_B√T с учетом фактов, изложенных в приложении 13.1, приведем формулу (26.9) к виду

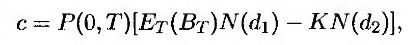
где

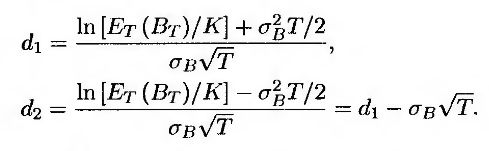
Учитывая формулу (26.10), приходим к усеченной формуле Блэка (26.5). Итак, мы показали, что если ожидаемая цена облигации установлена равной ее форвардной цене, то для дисконтирования размера выплаты следует использовать Т-летнюю текущую процентную ставку.