26.3. Процентные опционы “кэп” и “фло”

Одним из наиболее популярных процентных опционов, предлагаемых финансовыми организациями на внебиржевом рынке, является процентный опцион “кэп” (interest rate cap). Чтобы лучше понять его сущность, сначала следует рассмотреть вексель с плавающей ставкой (floating rate note), периодически устанавливаемой на уровне ставки LIBOR. Интервал времени между моментами установки процентной ставки называется расчетным (tenor). Предположим, что расчетный интервал равен трем месяцам. Процентная ставка по векселю на первые три месяца равна первоначальной трехмесячной ставке LIBOR, процентная ставка по векселю на следующие три месяца равна трехмесячной ставке LIBOR, доминирующей на рынке, и т.д.

Цель процентного опциона “кэп” (“шапка”. – Примеч. ред.) – застраховаться от того, что доходность по плавающей ставке превысит определенный уровень. Этот уровень называется предельным (cap rate). Допустим, что основная сумма равна 10 млн долл., расчетный интервал (tenor) векселя равен трем месяцам, продолжительность опциона равна пяти годам, а предельный уровень равен 4%. (Поскольку выплаты осуществляются поквартально, предельный уровень устанавливается с учетом поквартального начисления.) Опцион “кэп” представляет собой страховку от того, что плавающая процентная ставка поднимется выше 4%.

Пока мы будем игнорировать календарные поправки и предположим, что между моментами выплат проходит ровно 0,25 года. Календарные поправки будут рассмотрены в конце этого раздела. Предположим также, что в момент установки процентной ставки трехмесячная ставка LIBOR равна 5%. Таким образом, через три месяца размер выплаты по векселю с плавающей ставкой составит

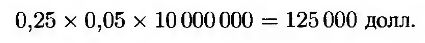
Если бы ставка LIBOR была равна 4%, размер выплаты был бы равен

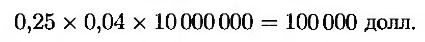
Таким образом, выигрыш по опциону “кэп” равен 25 000 долл. Обратите внимание, что выигрыш происходит не в день установки новой процентной ставки, а на три месяца позже. Это отражает существование обычного временного лага между наблюдаемой процентной ставкой и соответствующими выплатами.

В каждый момент установки новой процентной ставки на протяжении срока действия опциона регистрируется значение ставки LIBOR. Если ставка LIBOR меньше 4%, то через три месяца опцион “кэп” не принесет никакого выигрыша. Если же ставка LIBOR больше 4%, то через квартал выигрыш будет равен сумме, полученной путем применения четверти избыточной процентной ставки к основной сумме. Обратите внимание на то, что опцион “кэп”, как правило, организовывается так, чтобы первоначальная ставка LIBOR, даже если она превышает предельный уровень, не приносила немедленного выигрыша. В нашем примере опцион “кэп” длится пять лет. Следовательно, на протяжении срока его действия будет 19 моментов, в которых процентная ставка устанавливается заново (в моменты 0,25, 0,5, 0,75, ..., 4,75 лет), и 19 потенциальных выигрышей (в моменты 0,50, 0,75, 1,00, ..., 5,00 лет).

Опцион “кэп” как портфель, состоящий из процентных опционов

Рассмотрим опцион “кэп”, срок действия которого равен Т, основная сумма равна L, а предельный уровень равен R_K. Предположим, что новые процентные ставки устанавливаются в моменты t₁, t₂, ..., t_n. Пусть t_n+1 = Т. Обозначим через R_k процентную ставку, установленную на промежуток времени между моментами t_k и t_k+1 и наблюдаемую в момент t_k (1 ≤ k ≤ n). Выигрыш по опциону “кэп” в момент t_k+1, k = 1, 2, ..., п, равен

где δ_k = t_k+1 – t_k. (Величины R_k и R_K устанавливаются с учетом того, что частота начисления равна частоте изменения процентных ставок.)

Формула (26.11) описывает выигрыш по опциону “колл”, возникающий в момент t_k+1, при ставке LIBOR, наблюдаемой в момент t_k. Опцион “кэп” представляет собой портфель таких опционов. Ставки LIBOR регистрируются в моменты t₁, t₂, ..., t_n, а соответствующие выигрыши возникают в моменты t₂, ..., t_n, t_n+1. Компоненты опциона “кэп” называются кэплетами (caplets).

Опцион “кэп” как портфель облигационных опционов

Процентный опцион “кэп” можно представить в виде портфеля опционов на продажу облигаций с нулевым купоном, выигрыши по которым возникают непосредственно в момент их подсчета. Выигрыш в формуле (26.11) в момент t_k+1 эквивалентен величине

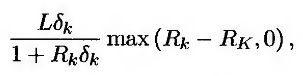
вычисленной в момент t_k. Простыми алгебраическими преобразованиями это выражение можно свести к следующему.

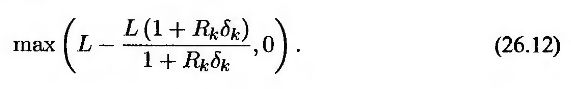
Дробь

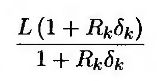
Представляет собой зарегистрированную в момент t_k стоимость облигации с нулевым купоном, выплата по которой в момент t_k+1 равна L(1 + R_Kδ_k). Следовательно, выражение в формуле (26.12) представляет собой выигрыш по опциону на продажу облигации с нулевым купоном, срок обращения которой истекает В момент t_k+1, а номинальная стоимость равна L(1 + R_Kδ_k), при условии что срок действия опциона истекает в момент t_k, а цена исполнения опциона равна L. Таким образом, процентный опцион “кэп” можно интерпретировать как портфель европейских опционов на продажу облигаций с нулевым купоном.

Опционы “фло” и “коллар”

Процентные опционы “фло” и “коллар” (иногда их также называют рамочными соглашениями (floor-ceiling agreement)) аналогичны опциону “кэп”. Опцион “фло” (“пол”. – Примеч. ред.) приносит выигрыш, когда процентная ставка по соответствующему векселю с плавающей ставкой падает ниже установленного уровня. Используя введенные ранее обозначения, можно выигрыш по опциону “фло” в момент t_k+1, где k = 1, 2,..., п, вычислить по формуле

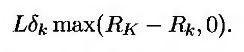
Аналогично процентному опциону “кэп”, процентный опцион “фло” можно представить в виде портфеля опционов на продажу процентных ставок либо в вида портфеля, содержащего опционы на покупку облигаций с нулевым купоном. Компоненты опциона “фло” называются флорлетами (floorlets). Опцион “коллар” (“ошейник”. – Примеч. ред.) представляет собой финансовый инструмент, цель которого – гарантировать, что плавающая процентная ставка по соответствующему векселю всегда лежит в определенном диапазоне. Опцион “коллар” является комбинацией длинной позиции по опциону “кэп” и короткой позиции по опциону “фло”. Он часто конструируется так, чтобы цена опциона “кэп” в начальный момент времени была равна цене опциона “фло”. Таким образом, стоимость заключения опциона “коллар” равна нулю.

Как показано во врезке “Пример из деловой практики 26.1”, между ценами опционов “кэп” и “фло” существует паритет опционов “колл” и “пут”.

Пример из деловой практики 26.1. Паритет опционов “кэп” и “фло”

Между ценами опционов “кэп” и “фло” существует паритет опционов “колл” и “пут”. Это значит, что

цена опциона “кэп” = цена опциона “фло” + стоимость свопа.

В этом равенстве опционы “кэп” и “фло” имеют одинаковые цены исполнения R_K. Своп – это соглашение получить плавающую ставку и заплатить фиксированную ставку R_K, не обмениваясь выплатами в первый момент установки новой процентной ставки. Все три инструмента имеют одинаковую продолжительность и одну и ту же частоту выплат.

Чтобы убедиться в этом, рассмотрим сочетание длинной позиции в опционе “кэп” с короткой позицией в опционе “фло”, создавая те же денежные потоки, что и своп. В течение периодов времени, на которых ставка LIBOR превышает величину R_K, опцион “кэп” порождает платежи в размере LIBOR – R_K. В течение периодов времени, на которых ставка LIBOR меньше величины R_K, короткая позиция по опциону “фло” порождает платежи в размере – (R_K – LIBOR) = LIBOR – R_K. Следовательно, при любом развитии событий размер платежей равен LIBOR – R_K. ЭТИ платежи представляют собой денежные потоки в рамках свопа. Таким образом, стоимость опциона “кэп” за вычетом стоимости опциона “фло” должна быть равной стоимости соответствующего свопа.

Обратите внимание на то, что свопы обычно конструируются так, чтобы выплаты в первый момент установки новой процентной ставки определялись ставкой LIBOR, зарегистрированной в нулевой момент времени. Опционы “кэп” и “фло” обычно конструируются так, чтобы они не приносили выигрыша в этот момент. Вот почему своп должен быть определен таким образом, чтобы в первый момент установки новой процентной ставки никакие выплаты не производились.

Оценка опционов “кэп” и “фло”

Как следует из формулы (26.11), кэплет, соответствующий процентной ставке, зарегистрированной в момент t_k, приносит в момент t_k+1 выигрыш

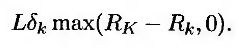
Если процентная ставка R_k имеет логнормальное распределение с волатильностью σ_k, то из формулы (26.3) следует, что стоимость этого кэплета равна

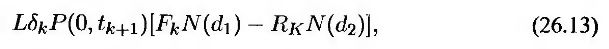
где

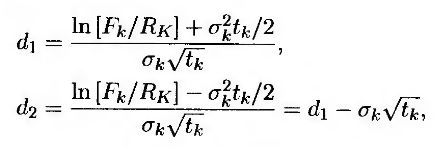
a F_k – форвардная ставка, установленная на период между моментами t_k и t_k+1. Из формулы (26.4) следует, что стоимость соответствующего флорлета равна

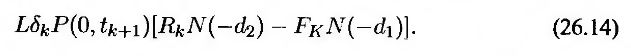
Пример 26.3

Рассмотрим трехмесячный контракт, в котором предельный уровень процентной ставки по займу на 10000 долл. равен 8% годовых (при ежеквартальном начислении), а срок не выходит за пределы одного календарного года. Этот контракт представляет собой кэплет и может быть элементом опциона “кэп”. Предположим, что кривая доходности является плоской и проходит на уровне 7% годовых при ежеквартальном начислении, а однолетняя волатильность трехмесячной процентной ставки, лежащей в основе кэплета, равна 20% в год. Нулевая процентная ставка с непрерывным начислением для всех сроков погашения равна 6,9394%. Таким образом, параметры в формуле (26.13) имеют следующие значения: F_k = 0,07, δ_k = 0,25, L = 10000, R_K = 0,08, t_k = 1, 0, t_k+1 = 1,25, P(0, t_k+1) = e^{-0,069394x1,25} = 0,9169 и σ_k = 0,20. Кроме того,

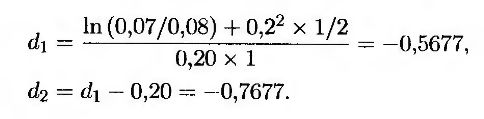
Таким образом, стоимость кэплета равна

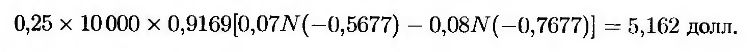
(Обратите внимание на то, что стоимость кэплета, вычисленная с помощью программы DerivaGem, равна 5,146 долл. Это объясняется тем, что в программе DerivaGem заложено предположение, что год состоит из 365 дней и она округляет время до ближайшего целого числа дней.)

Каждый кэплет в опционе “кэп” должен оцениваться по формуле (26.13) отдельно от других. С одной стороны, для каждого кэплета можно установить отдельную волатильность – так называемую реальную волатильность (spot volatility). С другой стороны, для всех кэплетов, образующих опцион “кэп”, можно установить одну и ту же волатильность, но варьировать ее в зависимости от срока действия опциона. Такая волатильность называется слабой, или плоской (flat volatility). На рынке, как правило, используются слабые волатильности. Однако многие трейдеры предпочитают работать с реальной волатильностью, поскольку она позволяет выявлять недооцененные и переоцененные кэплеты. Опционы на продажу или покупку фьючерсов на евродоллары очень напоминают кэплеты, а реальные волатильности, используемые для оценки кэплетов с трехмесячной ставкой LIBOR, часто сравнивают с волатильностями, вычисленными по ценам фьючерсных опционов на поставку евродолларов.

Реальная и слабая волатильности

Типичная зависимость реальной и слабой волатильности от срока действия соответствующего опциона продемонстрирована на рис. 26.3. (Для реальной волатильности этим сроком действия считается срок действия кэплета, а для слабой волатильности он совпадает со сроком действия опциона “кэп”.) Слабая волатильность сродни среднему значению реальных волатильностей и поэтому имеет меньшую изменчивость. Как показано на рис. 26.3, график волатильности, как правило, имеет “горб”. Вершина этого горба приходится на второй или третий год. Этот “горб” характерен как для волатильности, подразумеваемой при оценке опциона, так и для волатильности, вычисленной по ретроспективным данным. Относительно причин его существования единой точки зрения не существует. Одно из возможных объяснений этого явления заключается в следующем. Процентные ставки, соответствующие краткосрочным кривым доходности, контролируются центральными банками. И наоборот, двухлетние и трехлетние процентные ставки определяются, в основном, торговой деятельностью трейдеров. Эти трейдеры могут излишне резко реагировать на изменения на колебания краткосрочных ставок, что приводит к относительному повышению волатильности двухлетних и трехлетних ставок. Если срок действия опциона превышает два или три года, то процесс возвращения процентных ставок к среднему значению, объясняемый в главе 28, приводит к уменьшению их волатильности.

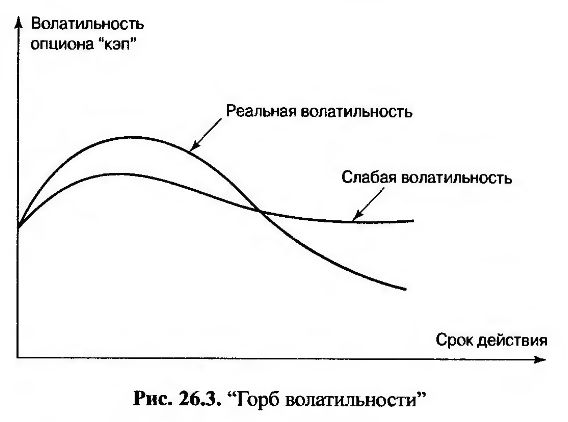
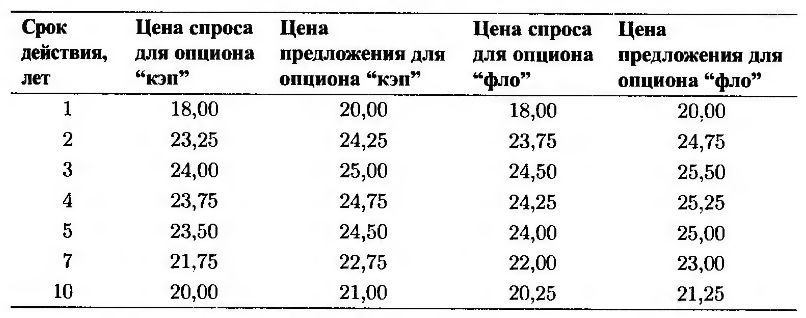
Брокеры пользуются таблицами, содержащими значения подразумеваемой волатильности для опционов “кэп” и “фло”. Инструменты, на основе которых рассчитываются эти котировки, как правило, приносят выигрыш. Это значит, что процентные ставки по опционам “кэп” и “фло” эквивалентны процентной ставке по свопу, сроки выплат по которому совпадают со сроками выплат по опциону “кэп”. В табл. 26.1 приведены брокерские котировки, типичные для денежного рынка США. Срок действия процентных ставок по опционам “кэп” равен трем месяцам, а их продолжительность варьируется от одного до десяти лет. Эти данные подтверждают существование “горба”, изображенного на рис. 26.3.

Теоретическое обоснование модели

Докажем внутреннюю непротиворечивость модели Блэка для оценки кэплетов, рассмотрев форвардные риск-нейтральные условия относительно облигации с нулевым купоном, срок обращения которой истекает в момент t_k+1. Анализ фактов, изложенных в разделе 25.4, приводит к следующим выводам, справедливым для этих условий.

1. Текущая стоимость любой ценной бумаги равна ее стоимости, ожидаемой в момент t_k+1, умноженной на ее стоимость в этот момент (см. равенство (25.20)).

2. Ожидаемое значение процентной ставки, установленной на период времени между моментами t_k и t_k+1 равно форвардной процентной ставке (см. равенство (25.22)).

Первый из этих результатов означает, что цена кэплета, приносящего выигрыш в момент t_k+1, равна

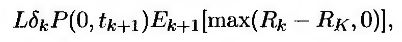
где E_k+1 – математическое ожидание в форвардных риск-нейтральных условиях относительно облигации с нулевым купоном, срок обращения которой истекает в момент t_k+1. С учетом фактов, изложенных в главе 13, эту стоимость можно записать следующим образом.

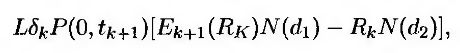
где

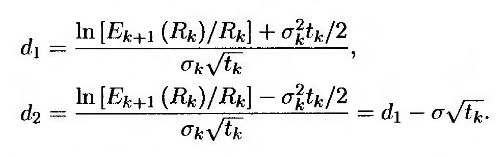
Из второго утверждения следует, что

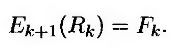
Сочетание этих результатов приводит к модели для оценки опциона “кэп” с помощью равенства (26.13). Они означают, что выигрыш следует дисконтировать на величину t_k-летней процентной ставки, зарегистрированной на рынке в текущий момент при условии, что ожидаемая процентная ставка установлена на уровне форвардной.

Использование программы DerivaGem

Для вычисления стоимости процентных опционов “кэп” и “фло” с помощью модели Блэка можно использовать программу DerivaGem. Для этого на рабочем листе Cap_and_Swap_Option в раскрывающихся списках Underlying Туре и Pricing Model следует выбрать пункты Cap/Floor и Black-European. Кривая нулевой доходности вводится с учетом непрерывных начисляемых процентных ставок. К входной информации относятся начальная и конечная даты действия опциона “кэп”, а также частота установок процентной ставки (т.е. длина расчетного интервала). Вычисления в программе выполняются в направлении от конца срока действия опциона “кэп” к его началу. Считается, что первоначальные кэплеты и флорлеты охватывают период, длина которого колеблется от 0,5 до 1,5 длины регулярного периода. Предположим, например, что период действия опциона “кэп” колеблется от 1,2 до 2,8 лет, а процентные ставки устанавливаются ежеквартально. Существует шесть кэплетов, покрывающих периоды от 2,55 до 2,80 лет, от 2,30 до 2,55 лет, от 2,05 до 2,30 лет, от 1,80 до 2,05 лет, от 1,55 до 1,80 лет и от 1,20 до 1,55 лет.

Влияние календарных поправок

Формулы, приведенные выше, не учитывают календарных поправок (описание календарных поправок содержится в разделе 6.1). Предположим, что верхний предельный уровень R_K установлен с учетом коэффициента “длина расчетного периода/360” (как это принято в США). Это значит, что длину временного интервала δ_k следует заменить величиной α_k, представляющей собой период накопления (accrual fraction) на интервале времени от t_k до t_k+1. Предположим, например, что момент t_k приходится на 1 мая, а момент t_k+1 – на 1 августа. Применение коэффициента “длина расчетного периода/360” означает, что между этими моментами выплат проходит 92 дня. Следовательно, α_k = 92/360 = 0,2521. Форвардную ставку также следует вычислять с учетом коэффициента “длина расчетного периода/360”. Это значит, что для ее вычисления необходимо применять формулу

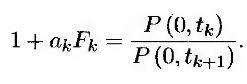
Результат этих расчетов эквивалентен преобразованию величины R_k, вычисленной с учетом коэффициента “длина расчетного периода/360”, в величину R_k, вычисленную с учетом коэффициента “длина расчетного периода/длина расчетного периода”. Кроме того, величина должна вычисляться с учетом коэффициента “длина расчетного периода/длина расчетного периода”. Иначе говоря, это эквивалентно вычислению коэффициента R_k путем умножения котировочной стоимости опциона “кэп” на коэффициент 365/360 или 366/360 и определению величины F_k по формуле
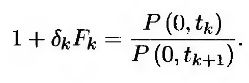