|
До сих пор мы оценивали эффективность критерия путем построения регрессионной зависимости между показателями критерия и реализовавшейся прибыли. В качестве показателя эффективности использовался коэффициент детерминации, отражающий меру вариации данных вокруг линии регрессии. Хотя коэффициент детерминации адекватно отражает меру зависимости прибыли от критерия, он ничего не говорит о форме этой зависимости. Проиллюстрируем вышесказанное на гипотетическом идеализированном примере. Предположим, что мы оцениваем три выборки, каждая из которых состоит из десяти комбинаций, построенных по определенной стратегии. Применяя к каждой выборке один и тот же критерий, нужно определить, какова эффективность критерия при отборе комбинаций для каждой из трех стратегий.
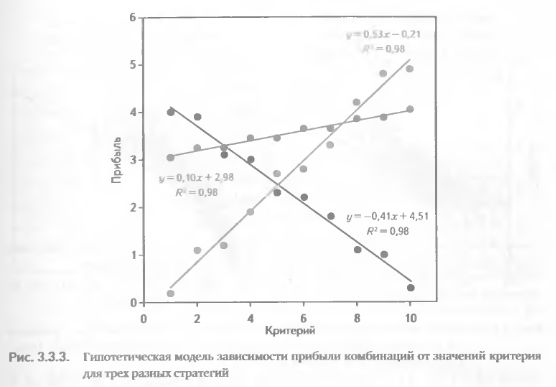
Мы смоделировали данные таким образом, чтобы в каждом случае коэффициент детерминации оказался очень высоким и был одинаковым для всех трех стратегий. Казалось бы, можно сделать вывод об одинаковой эффективности критерия применительно к каждой из стратегий. Однако рассмотрение графика регрессионных зависимостей указывает на преждевременность таких выводов (рис. 3.3.3).


В одном случае прибыль комбинаций растет быстрыми темпами по мере роста критерия. В другом случае наблюдается гораздо более медленный рост. И, наконец, в третьем случае увеличение значений критерия сопровождается падением прибыли комбинаций. Принимая во внимание такие формы зависимости {критерий х прибыль}, следует заключить, что данный критерий наиболее эффективен применительно к первой стратегии, менее эффективен для второй и полностью непригоден для третьей стратегии. Однако использованный нами показатель (коэффициент детерминации) указывает на абсолютно одинаковую эффективность данного критерия во всех трех ситуациях!
Это говорит о необходимости представления показателя эффективности критерия в ином виде, учитывающем не только силу зависимости прибыли от критерия, но и форму этой зависимости. Форма зависимости определяется уравнением регрессии, в котором для нас наибольшее значение имеет коэффициент наклона линии регрессии (угловой коэффициент). В рассмотренной выше модели угловой коэффициент был наибольшим для первой стратегии (0,53), несколько меньшим для второй (0,1) и наименьшим для третьей стратегии (-0,41) (рис. 3.3.3).
Таким образом, представляется целесообразным выражать показатель эффективности критерия одновременно в двух видах: как коэффициент детерминации (что отражает силу взаимосвязи критерия и прибыли) и как угловой коэффициент (что отражает форму этой взаимосвязи). Вместе с тем, необходимо иметь в виду, что при моделировании гипотетической ситуации, представленной на рис. 3.3.3, мы подобрали данные таким образом, чтобы коэффициенты детерминации во всех случаях были одинаковы и не зависели от угловых коэффициентов. Поэтому будет полезно исследовать взаимозависимость этих двух разновидностей показателя эффективности критерия на реальных данных.
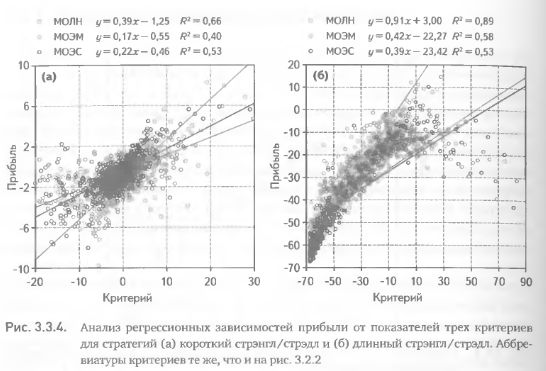
Рассмотрим регрессионные зависимости {критерий х прибыль} для трех критериев (математические ожидания прибыли по логнормальному (МОЛН), эмпирическому (МОЭМ) и симметризованному эмпирическому (МОЭС) распределениям) применительно к двум разнонаправленным опционным стратегиям (короткий и длинный стрэнгл/стрэдл). Вновь воспользуемся значениями параметров, установленными в предыдущих разделах: 100-дневный диапазон усреднения и 500 задействованных в анализе комбинаций. В случае как длинной, так и короткой стратегии наибольшее значение показателя эффективности критерия, выраженного посредствам коэффициента детерминации, было получено для критерия МОЛН. Выражение показателя эффективности в альтернативной форме, через угловой коэффициент, показало тот же результат– Для обеих стратегий максимальное значение коэффициента достигалось при оценке комбинаций по критерию МОЛН (рис. 3.3.4). На втором месте находится критерий МОЭМ. И вновь это оказалось справедливо для обеих форм показателя эффективности. Последнее место занимает критерий МОЭС, для которого так же наблюдается согласованность двух видов показателя эффективности рис. 3.3.4).
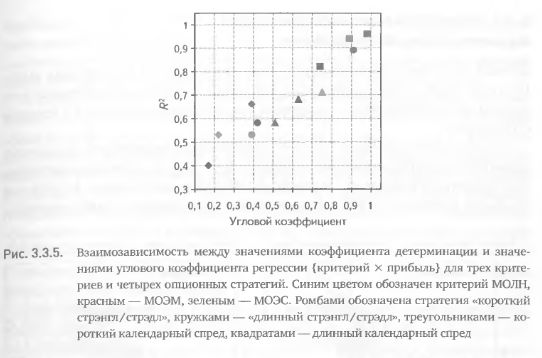
Суммируя вышесказанное, можно заключить, что в исследованных случаях существует положительная взаимозависимость между значениями коэффициента детерминации и значениями углового коэффициента. Это наводит на мысль о том, что обе формы выражения показателя эффективности оценивают прогностические качества критериев приблизительно одинаково. Для того чтобы убедиться в этом, рассчитаем регрессии, аналогичные представленным на рис. 3.3.4, еще для двух стратегий, короткий и длинный календарный спред. Вычислив для каждой регрессии значения обоих коэффициентов и воспользовавшись ранее полученными данными, построим график зависимости коэффициентов детерминации от угловых коэффициентов.
Наши предположения оказались верны. В исследованных случаях существует очень сильная взаимозависимость между двумя видами данного показателя эффективности (рис. 3.3.5). Следовательно, оценивая эффективность критерия с помощью коэффициентов регрессии {критерий х прибыль}, допустимо ограничиться расчетом лишь одного из них. Вместе с тем следует иметь в виду, что при оценке других критериев и использовании их в работе с другими стратегиями можно столкнуться с иными видами зависимости между различными формами выражения определенного показателя эффективности. Может также обнаружиться полное отсутствие взаимозависимости. В таких случаях полезно использовать все возможные формы выражения показателя эффективности, поскольку информация, содержащаяся в каждом из них, будет не дублирующей, а взаимодополняющей.
|