|
Эта таблица дает возможность получить некоторые из тех результатов матрицы риска, которые были описаны в седьмой главе. Одна из них — Таблица 7.3 — приведена здесь в целях облегчения изложения. Прилагаемый файл содержит точно такой же портфель, а именно: состоящий из короткой позиции на 200 трехмесячных опционов пут с ценой страйк $95, длинной позиции на 100 трехмесячных опционов пут с ценой страйк $105 и длинной позиции на 100 шестимесячных опционов колл с ценой страйк $115. Для упрощения мы будем использовать этот портфель, чтобы объяснить все значения таблицы, представляющей оценку рисков. Как позже станет ясно, мы можем увеличить позицию, чтобы она содержала до девяти цен исполнения и три различных жизненных цикла опциона. Опытный пользователь сможет усовершенствовать файл с тем, чтобы увеличить количество включаемых цен страйк и циклов жизни опциона.
Таблица занимает 14 листов. Фронтальный, или первый, лист содержит все исходные данные, а также результаты матрицы риска, которые даны выше. Математические вычисления производятся на каждом из остальных 13 листов. Каждый из 13 листов содержит информацию, относящуюся к 13 рядам Таблицы 7.3, а каждый из 13 рядов соответствует возможным различным ценам акции. 13 листов (Sheet 3, Sheet 4,...., Sheet 15) содержат абсолютно одинаковую формулу. Листы отличаются только тем, что значение, вводимое в ячейку В1 является ценой акции, соответствующей той, что приведены в краткой матрице рисков. Поэтому в данном примере ячейка В1 на Sheet 3 содержит цену акции 76, ячейка В1 на Sheet 4 содержит цену акции 80, и так далее — до Sheet 15, на котором ячейка В1 содержит цену акции 124. Sheet 2 оставлен пустым. Теперь рассмотрим фронтальный, или первый, лист — Sheet 1.
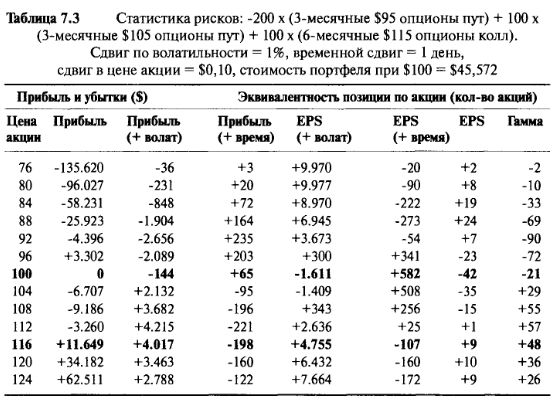


Лист 1. Общая информация и позиция Портфеля
Область А1 . . . G70 содержит самое большое количество вводимых в нее данных. Некоторые из вводимых переменных обозначены простыми числами, а многие имеют различные имена. Остальные переменные даны в виде векторов или диапазонов, которым также присвоены имена.
Основные простые числа, вводимые в качестве переменных
Ниже приводится краткое описание каждого простого числа, вводимого в качестве переменной каждой ячейки, а также название и примеры значений.
-Ячейка ВЗ (smid) — центральная цена акции, которая возникает, как результат вычисленной матрицы риска. Обычно есть смысл избрать текущую цены акции как центральную цену. Таблица результатов, таким образом, отражает разные свойства риска при ценах акций вокруг центральной цены. В данном примере это значение установлено как 100.
-Ячейка D3 (sdif) — разница в цене. Значение обуславливает диапазон различных цен акций, использованных в создании матрицы риска. В данном примере значение установлено как 4, поэтому разница между каждой последующей ценой составляет $4. Таким образом, мы имеем 13 различных цен акций: $76, $80, $84, ..., $124, которые вычисляются с помощью: (smid-б * sdif), (smid-5 * sdif), (smid-4 * sdij),..., (smid+6 * stif).
-Ячейка Dl имеет функцию TODAY (), которая выдает текущую дату в соответствующем формате. Это требуется для вычисления времени, оставшегося до истечения срока различных опционов.
-Ячейка D2 (rate) — соответствующая процентная ставка. В данном примере она установлена на нуль.
-Ячейка D4 — параметр для тэты - разница в днях. В данном примере это значение установлено как один день, поэтому результирующие значения в колонках (+ time) представляют изменение в P&L или дельте, вызванное истечением одного дня.
-Ячейка F4 (tdif) - параметр для тэты — разница, которая используется во всех последующих математических вычислениях. Соответственно, он выражен в долях года и наделен знаком минус. Это значение вычисляется из вводимого значения в ячейку D4 при использовании выражения: [= —D4/365].
-Ячейка D5 (vdif) — параметр для веги - разница. В данном примере это значение установлено как 0,01 или 1%, поэтому результирующие значения в колонках (+ vol) представляют изменения в P&L или дельте, вызванное увеличением волатильности на 1%.
-Ячейка D6 (gdif) параметр для гаммы — разница, в данном примере установлена как 0,10. При такой установке вводимые значения в колонку гаммы для матрицы риска отражают изменения в экспозиции акции, вызванные увеличением в цене базовой акции на $0,10, или 10 центов.
-Ячейка D7 (mult) — мультипликатор опциона. В данном примере он установлен на 100, так как опционы, описанные в книге, исполняются на 100 акций. Различные опционные рынки имеют разное количество акций за опцион. Опционные контракты на акции в Великобритании и Австралии, например, исполняются на 1.000 акций. Многие опционы на фьючерсные контракты исполняются лишь на один фьючерс.
-Ячейка В5 (ssz) - позиция по акции. Часто сложные опционные портфели содержат также еще и длинную или короткую позицию на базовую акцию. Если рассматриваемый портфель имеет короткую позицию, скажем на 5.000 акций, тогда следует ввести значение "—5.000" в эту ячейку. В данном примере эта ячейка установлена на нуль, так как портфель не имеет позицию по акции.
-Ячейка В6 (spr) — средняя цена акции. В данном примере это не имеет значения, поэтому цена установлена на нуль. Однако, если скажем, портфель имел короткую позицию на 5.000 акций, тогда среднее значение цены должно быть введено в эту ячейку. Например, допустим, что позиция по акции была введена в результате продажи в шорт 2.000 акций по $100 и 3.000 акций по $110. Тогда средняя цена акции, вводимая в ячейку В6, должна быть следующей:
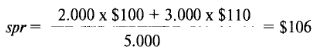
-Ячейка В7 (scost) — стоимость введения позиции по акции. Стоимость ввода позиции на акции вычисляется из параметра числа днейдля тэты в годовом представлении, процентной ставки, средней цены акции и позиции по акции, путем использования следующего выражения:
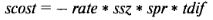
В данном примере значение, очевидно, является нулевым, но давайте рассмотрим ситуацию, когда портфель имеет короткую позицию на 5.000 акций по средней стоимости $106. Если процентная ставка равна 10%, а параметр тэта установлен как 1 день, то это означает, что стоимость введения позиции на акцию будет составлять:
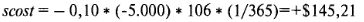
Позиция имеет чистую положительную стоимость ее ввода. Короткая позиция приносит доход $145,21в день. При больших позициях на акцию эта стоимость имеет значительное влияние в колонке (+time) в разделе P&L матрицы риска.
Специфические переменные, определяющие параметры истечения, вводимые как единичные числа.
Рассматриваемая таблица RISK1.XLS имеет три разных цикла срока истечения, размещенных в областях A9...G24, A32...G47 и A55...G70 соответственно. Основные переменные, связанные с первым циклом и вводимые как простые числа, следующие:
-Ячейка D9 — дата истечения срока в требуемом формате для опционов с циклом № 1.
-Ячейка D10 — количество дней, оставшихся до срока истечения этого цикла. Вычисляется как разница между ячейкой D9 и текущей датой в ячейке D1.
-Ячейка D11 (time1) время, оставшееся до срока истечения опционов с циклом № 1, выраженное в годах и являющееся просто количеством дней, разделенным на 365. Переменная time1 является простым переменным числом, которое применяется во всей таблице при обращении к позиции опционов из первого цикла.
Ячейки в диапазонах, содержащих циклы срока истечения №2 и №3 опционных позиций, имеют подобные вводные значения. Переменные простых чисел, соответствующие времени до срока истечения (в годах), есть time2 и timeЗ соответственно. Для того чтобы точно продублировать цифры в Таблице 7.3, необходимо изменить даты срока истечения таким образом, чтобы количество дней, оставшихся до наступления срока истечения, соответствовало значениям 90,182 и 272 соответственно.
Специфические переменные параметров истечения, или векторы, вводимые в области
Для того чтобы упростить математические выражения, таблица прибегает к функции переменной диапазона Microsoft Excel. Это позволяет рассматривать колонку (или ряд) чисел как простые математические выражения. Таблица имеет 6 таких функций переменных диапазона:
-Диапазон: С16...С70 (exprice) - группа цен исполнения для всех циклов срока истечения.
-Диапазон В16...В70 (vol) — группа отдельных волатильностей. В данном примере каждый элемент установлен на 15%, но пользователь может установить каждую волатильность как отдельные значения.
-Диапазон D16....D70 (putsz) — группа позиций, определяющих позицию на опционы пут для всех истекающих циклов и всех цен исполнения. В данном примере портфель содержит короткую позицию на 200 краткосрочных (три месяца) опционов пут с ценой страйк $95 и длинную позицию на сто краткосрочных (три месяца) опционов пут с ценой страйк $105. Соответственно ячейка D18 имеет вводное значение -200, а ячейка D20 — вводное значение +100, в то время как остальные ячейки установлены на нуль.
-Диапазон F16...F70 (callsz) — группа позиций, определяющих позицию по опционам колл для всех циклов срока истечения и всех цен страйк. В данном примере портфель содержит длинную позицию на 100 среднесрочных (шесть месяцев) опционов колл с ценой страйк $115. Соответственно, ячейка F45 имеет вводное значение +100, в то время как остальные ячейки установлены на нуль.
-Диапазон Е16...Е70 (putpr) — используется для определения среднего значения цен исполнения для каждого пут опциона. Эти средние значения вычисляются таким же образом, как и средние значения цены акции. В данном примере средние значения трехмесячных пут опционов с ценами страйк $95 и $105 установлены как $1,05746 и $6,17616 соответственно.
-Диапазон G16...J70 (callpr) — используется для определения среднего значения цен исполнения для каждого опциона колл. В данном примере среднее значение 6-месячного опциона колл с ценой страйк $115 установлено как $0,49599.
Совсем не обязательно вводить две последние переменные putpr и callpr, так как они используются только для вычисления колонки P&L в матрице окончательного риска. Остальная матрица риска совершенно не зависит от этих цен.
Вся информация, необходимая для создания матрицы риска расположена на Sheet 1, описанном выше. И это все, что нужно знать, если вы не математик и не программист. Читатель может провести эксперименты в построении различных портфелей с использованием программы. Результирующие матрицы риска могут быть исследованы в табличной форме или путем построения графика. Читатели, не интересующиеся расчетами программы риска, могут сразу перейти к следующему разделу.
Лист 3 — Лист 15 Описание математических процедур
Математические вычисления проводятся на 13 отдельных листах: Sheet 3 —Sheet 15. Расположение всех листов идентично, но для демонстрации математических расчетов на всех листах мы будем впредь обращаться только к одному: Sheet 5.
Лист — цена акций
В Sheet 5, в самой первой ячейке В1, содержится формула [=smid — 4 * sdif], которая в данном примере означает: 100—4 * 4=84. Это цена акции для этого листа, и все свойства риска будут вычисляться по этому значению. В итоге результаты (всего их семь) будут переданы обратно на фронтальный лист и размещены в третий ряд матрицы риска (показывающем цену акции $84). Эта цена акций $84 используется на всем Sheet 5, поэтому наделена специальным значком: s
Детали опциона
Все переменные диапазона, относящиеся к ценам исполнения, вола-тильностям, размерам позиций и средним ценам, занимают соответствующие места. Поэтому ячейки В16...В70 на Sheet 5!Range имеют формулу [=vol], а все ячейки С16....С70 на Sheet 5!Range имеют формулу [=exprice], и т.д. Конечно, это совсем не обязательно, и занимает много лишнего места — ведь эти цифры повторяются на каждом из 13 листов. Однако, как определится ниже, иногда полезно (особенно для новичка) выявить особенные свойства риска каждого отдельного опциона при различных ценах акций. Наличие переменных опциона, таких как цена акции и вола-тильность, имеющихся на каждом листе, также вполне может пригодиться.
Все свойства каждой опционной позиции вычисляются при помощи математических выражений, идентичных формулам, представленным в таблице OPTIONS.XLS. Они включают в себя: (1) теоретическую цену, (2) вегу, (3) тэту, (4) дельту, (5) вегу дельты, (6) тэту дельты и (7) гамму. Вычисления требуют расчетов средних переменных, таких как argl, arg2, nd1, nd2, nd11, которые производятся в соответствующих рядах при помощи выражений, включающих в себя диапазоны переменных. Чтобы сэкономить место, эти средние переменные ничем не обозначаются, а рассматриваются везде только как обычные ячейки. Первым опционом с ненулевой позицией является опцион пут с ценой исполнения $95. Этот опцион располагается в 18 ряду, и формула, соответствующая средней переменной argl для этого опциона такова:
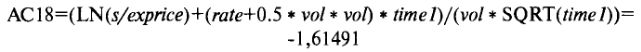
Эта переменная эквивалентна переменной argl в файле OPTIONS.XLS. Здесь же названная в формуле переменной s — локальная величина, и на Sheet 5 установлена как 84. Другие переменные: rate и time1 являются простыми числами. Переменная rate является процентной ставкой, участвующей во всех расчетах (в данном случае установлена как 0%), а переменная time1 является временем, оставшимся до истечения срока первого цикла (=90/365 года). Переменные диапазона exprice и vol относятся к вектору цен исполнения и связанной с ним волатильностью.
Хотя в выражении используются обозначенные переменные, достоинство Microsoft Excel в том, что при расчете используется только требуемая в данном случае величина. В примере, приведенном выше, формула располагается в 18 ряду Sheet 5, поэтому используемые соответствующие элементы ряда exprice и vol — являются значениями 95 и 0,15, соответственно. Ниже указаны остальные математические выражения, используемые для расчета каждой из соседних переменных для опционов с первым циклом. Также представляются результаты расчетов:
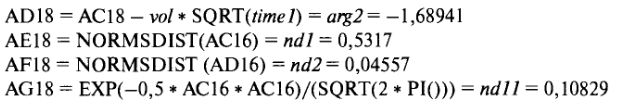
Чувствительности опциона вычисляются прямо из этих переменных, с использованием выражений, идентичных тем, что даны в файле OPTIONS.XLS.
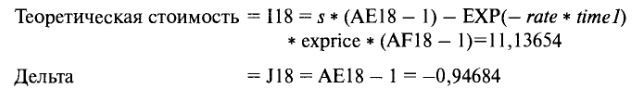
Итак, этот опцион при новой цене акции $84 теперь стоит 11,13654 и имеет новую дельту —0,94684. Этот опцион был первоначально продан в шорт при цене 1,05746, когда стоимость акции составляла $100. Это создает убыток, равный 11,13654 - 1,05746 = $10,07908 на каждую акцию. Размер позиции составляет 200 опционов, каждый из которых исполняется на сто акций, следовательно, общий убыток составляет 200 * 100 * 10,07908 = 201.582. Общее уравнение для P&L для этого опциона расположено в ячейке К18 и выглядит следующим образом:
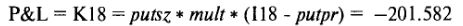
При цене акции $84 этот опцион имеет дельту - 0,94684. Портфель имеет в продаже шорт эту позицию, поэтому экспозиция по акции будет составлять 0,94684 за акцию. Размер позиции равен 200, поэтому чистая экспозиция по акции составит 200 * 100 * 0,94684 = +18.936. Общее выражение для экспозиции акций расположено в ячейке XI8 и выглядит следующим образом:
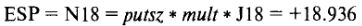
Математические выражения, ссылки на ячейки и результирующие значения каждой из пяти чувствительностей даны далее:

Эти цифры могут рассматриваться следующим образом:
-903: если волатильность увеличивается на значение vdif(1%), тогда эта рассматриваемая опционная позиция потеряет еще $903.
+75: когда проходит количество дней tdif(1 день), то этот данный опцион приносит прибыль, равную $75.
-244: если волатильность увеличивается на значение vdif( 1 %), тогда экспозиция позиции по акции для этого опциона уменьшится на 244 акции.
+20: когда проходит количество дней tdif (1день), тогда экспозиция позиции по акции для этого опциона увеличивается на 20 акций.
-35: если стоимость базовой акции увеличивается на значение gdif (0,1), тогда экспозиция по акции этого опциона увеличится на 35 акций.
Все вышеуказанные цифры были вычислены с использованием вводных значений для 18 ряда Sheet 5. Ряд 18 содержит информацию, относящуюся к короткой позиции из 200 трехмесячных опционов пут с ценой исполнения $95. Проверка 20-го ряда покажет, что идентичное выражение дает информация по длинной позиции на 100 трехмесячных опционов пут с ценой исполнения $105. Чувствительности, связанные с опционами колл, в частности: длинной позицией на 100 шестимесячных опционов колл с ценой исполнения $115, появляются в 45 ряду и в колонках S45 — АА45. Итоговое значение P&L, а также и все чувствительности просто суммируются друг с другом. Семь итоговых значений размещаются в ячейках от К77 до Q77. Таблица А. 1 суммирует статистические значения риска, взятые из Sheet 5, связанные с позицией при цене акции, установленной на $84.
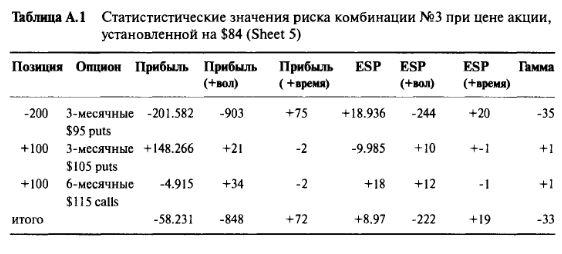
Затем все семь итоговых значений снова транспортируются на Sheet 1, в ряд, содержащий цену акции $84. Все это выполняется в Sheet 1 в ячейках I79 —Р79 с помощью использования следующего выражения: [=Sheet 5!$K77,=Sheet 5!$L77, и т. д.]. К колонкам P&L имеется несколько дополнительных компонентов, связанных с позицией акции.
Таким образом, теперь мы видим, как образуется результат на основе вводимых значений, соответствующие цене акции $84. На каждом листе происходит идентичным образом построенный процесс, но при условии, что каждый лист имеет различные значения для локальной переменной: s, цена акции. Тогда результирующей матрицей риска, воспроизведенной в Таблице 7.3, будет итоговое суммирование всех чувствительностей портфеля к изменениям волатильности, времени и цены акции.
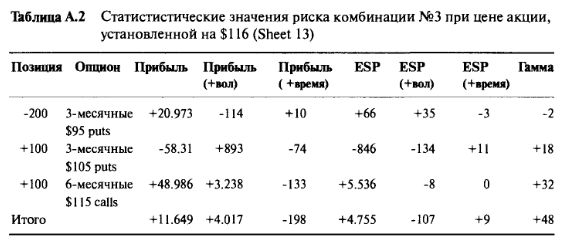
Истинное достоинство способа, с помощью которого построена таблица, заключается в том, что можно, хотя это и обременительно, и относительно медленно, произвести анализ каждого отдельного компонента. На Sheet 5, например, при цене акции $84 короткая позиция на опцион пут с ценой страйк $95 является явно доминирующим компонентом портфеля, с точки зрения экспозиции акции. На этом ценовом уровне акции, эта позиция вносит +18.936 акций экспозиции по акции и доминирует над другими двумя компонентами. Изучение Sheet 13, воспроизведенного в Таблице А.2, раскрывает, что при цене акции $116 экспозиция по акции значительно сокращена, достигнув +66 акций. При цене $116 пут опцион почти не вносит изменений.
Оформление таблицы RISK1.XLS явно не оптимальное. Имеется много дублирования и абсолютно не используются сложные функции макросов программы Microsoft Excel. Но автор сделал это специально. Хотя это и кажется обременительным, но все-таки достаточно просто можно использовать таблицу в той форме, в которой она дается. Однажды разобравшись, даже неопытный пользователь сможет точно заполнить таблицу. Два совета. Во-первых, копирование переменных диапазонов vol, exprice, putsz, putpr, callsz и callpr на Листах от 3 до 15 можно будет удалить. Во-вторых, можно выполнять расчет чувствительностей с помощью макросов.
|