|
Стоимость фондового опциона представляет собой функцию, зависящую от цены базовой акции и времени. Вообще говоря, стоимость любой производной ценной бумаги является функцией, зависящей от стохастических переменных и времени. Таким образом, необходимо обратить внимание на некоторые свойства функций, зависящих от стохастических аргументов. Важный результат в этой области был получен математиком Киёши Ито (Kiyosi Ito) в 1951 году. Он известен как лемма Ито.


Допустим, что значения переменной х подчиняются процессу Ито:
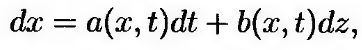 (12.11) (12.11)
где dz – винеровский процесс, а a и b – функции, зависящие от переменных х и t. Скорость дрейфа переменной х равна а, а дисперсия – b2. Лемма Ито утверждает, что существует некая функция G, зависящая от переменных х и t и подчиняющаяся стохастическому процессу
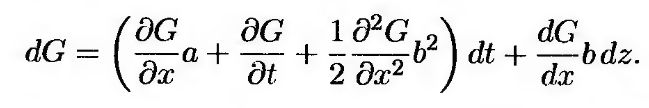 (12.12) (12.12)
Здесь dz – винеровский процесс из уравнения (12.11). Таким образом, функция G подчиняется процессу Ито. Ее дрейф равен
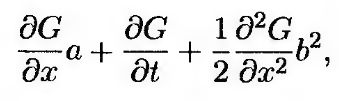
а дисперсия –
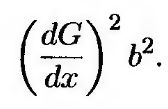
Строгое доказательство леммы Ито выходит за рамки нашей книги. В приложении 12.1 показано, что эту лемму можно интерпретировать как расширение известных результатов из дифференциального исчисления. Ранее мы утверждали, что модель
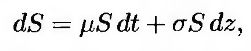 (12.13) (12.13)
где μ и σ – константы, хорошо описывает траекторию цены акции.
Из леммы Ито следует, что функция G, зависящая от цены акции S и времени t, подчиняется стохастическому процессу
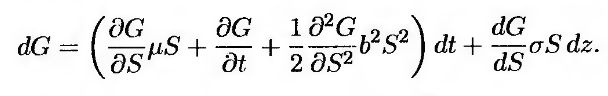 (12.14) (12.14)
Обратите внимание на то, что на значения S и G зависят от одного и того же источника неопределенности dz. Этот факт очень важен для доказательства результатов Блэка-Шоулза.
|